异配图神经网络——Graph Transformer Networks

一.论文概述

作者提出了Graph Transformer Network (GTN)用来在异配图（heterogeneous graph）上学习节点表示。通过Graph Transformer层，模型能将异构图转换为由meta-path定义的多个新图，这些meta-paths具有任意的边类型和长度，通过在学得的meta-path对应的新图上进行卷积能获取更有效的节点表示。在几个异配图数据集上的实验结果也验证了GTN的有效性。

二.预备知识

假设 ${\mathcal{T}}^v$和${\mathcal{T}}^e$ 分别表示节点类型和边类型，对于给定图$G=(V,E)$，其中$V$是节点集，$E$是边集，节点类型映射函数为$f_v:V\to {\mathcal{T}}^v$，边类型映射函数为$f_e:E\to {\mathcal{T}}^e$。当$\left|{\mathcal{T}}^e\right|=1$ 且$\left|{\mathcal{T}}^v\right|=1$时，图为同配图，否则为异配图。在本文中作者考虑$\left|{\mathcal{T}}^e\right|>1$的情况。异配图可以被表示为一个邻接矩阵 ${\left\{A_k\right\}}_{k=1}^K$ 的集合，其中$K=\left|{\mathcal{T}}^e\right|$，$A_k\in {\mathbf{R}}^{N\times N}$ 是一个邻接矩阵，当$A_k[i,j]$ 非零时，表示节点$j$到节点$i$间存在第$k$中类型的边。邻接矩阵的集合可以写为 $\mathbb{A}\in {\mathbf{R}}^{N\times N\times K}$，$X\in {\mathbf{R}}^{N\times D}$ 表示节点的$D$维特征组成的矩阵。

Meta-Path：异配图$G$上的连接异配边的路径$p$，如$v_1\stackrel{t_1}{⟶}{v}_2\stackrel{t_2}{⟶}\dots \stackrel{t_l}{⟶}{v}_{l+1}$，其中$t_l\in {\mathcal{T}}^e$表示meta-path的第$l$类边。Meta-path定义了节点$v_1$到$v_{l+1}$复合关系$R=t_1\circ t_2\dots \circ t_l$，其中$R_1\circ R_2$表示关系由$R_1$和$R_2$组成。给定复合关系$R$或边类型序列$\left(t_1,t_2,\dots ,t_l\right)$，meta-path $P$对应的邻接矩阵$A_{\mathcal{P}}$可以通过邻接矩阵乘法来获取：
$$A_{\mathcal{P}}=A_{t_l}\dots A_{t_2}{A}_{t_1}$$
meta-path的概念包含多跳连接，作者的框架中新图结构由邻接矩阵表示。

---

Graph Convolutional Network (GCN)：假设 $H^{(l)}$为GCN第$l$层的特征表示，则GCN的传播规则为：
$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
其中$\tilde{A}=A+I\in {\mathbf{R}}^{N\times N}$是添加了自环的邻接矩阵，$\tilde{D}$是与之对应的度矩阵。在GCN中图上的卷积操作由图结构来确定（图结构不可学习），只有节点的层特征表示包含一个线性变换$H^{(l)}{W}^{(l)}$。在作者的框架中，图结构是可以学习的，这使得可以从不同的卷积中获益。

对于有向图，作者采用入度对角矩阵来对$\tilde{A}$进行正则化，即${\tilde{D}}^{-\frac{1}{2}}\tilde{A}$。

三.Meta-Path的生成

先前的工作中meta-paths需要人工构造，而Graph Transformer Networks却可以通过给定的数据和任务来学习meta-paths，然后对学到的meta-paths进行图卷积。

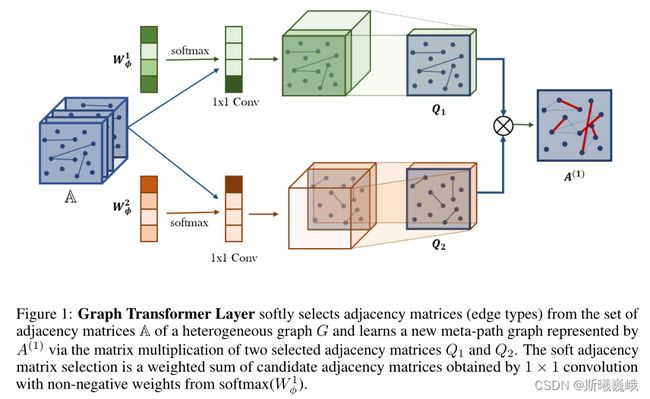
Graph Transformer (GT)层中meta-path的生成由两个组件。首先GT层从候选邻接矩阵$\mathbb{A}$中软选择两个图结构$Q_1$和$Q_2$，然后复合两种关系来学得一个新图结构（$Q_1$和$Q_2$间的矩阵乘法）。

软选择的具体过程：通过$1\times 1$卷积获取候选邻接矩阵的加权和，正式计算公式为：
$$Q=F\left(\mathbb{A};W_{\varphi }\right)=\varphi \left(\mathbb{A};\mathrm{softmax}\left(W_{\varphi }\right)\right)$$
其中$\varphi$是卷积层，$W_{\varphi }\in {\mathbf{R}}^{1\times 1\times K}$是$\varphi$的参数。加上$\text{softmax}$能获取类似channel attention的效果。

另外，在生成meta-path邻接矩阵时为了数值稳定，作者还使用度矩阵来对其进行正则化，即$A^{(l)}=D^{-1}{Q}_1{Q}_2$。

---

理论证明：GTN是否可以学到关于边类型和路径长度的任意meta-path

任意长度为$l$的元路径对应的邻接矩阵$A_P$可以通过如下公式计算得到：
$$A_P=\left(\sum _{t_1\in {\mathcal{T}}^e}{\alpha }_{t_1}^{(1)}{A}_{t_1}\right)\left(\sum _{t_2\in {\mathcal{T}}^e}{\alpha }_{t_2}^{(2)}{A}_{t_2}\right)\cdots \left(\sum _{t_l\in {\mathcal{T}}^e}{\alpha }_{t_l}^{(l)}{A}_{t_l}\right)$$
其中${\alpha }_{t_l}^{(l)}$表示第$l$个GT层中边类型$t_l$对应的权重，$A_P$可以看作所有长度为$l$的元路径邻接矩阵的加权和，因此堆叠$l$个GT层能够学习任意长度为$l$的meta-path结构（参见图2）。

这也存在一个问题，添加GT层会增加meta-path的长度，这将使得原始边被忽略。在一些应用中，长meta-path和短meta-path都很重要，为了学习短和长元路径（包括原始边），作者在候选邻接矩阵中添加了单位阵。该trick使得当堆叠$l$个GT层时，允许GTN学习任意长度的meta-path，最长可达$l+1$。

四.Graph Transformer Networks

同普通的图像卷积类似，可以使用多个卷积核（作者设置为$C$）来同时考虑多种类型的meta-path，然后生成一个meta-paths集，中间邻接矩阵$Q_1$和$Q_2$则变成邻接张量${\mathbb{Q}}_1$ 和${\mathbb{Q}}_2\in {\mathbf{R}}^{N\times N\times C}$（参见图2）。通过多个不同的图结构学习不同的节点表示是有益的。作者在堆叠了$l$个GT层之后，在meta-path张量的每个channel上应用相同的GCN，然后将多个节点特征进行拼接：
$$Z={\Vert }_{i=1}^C\sigma \left({\tilde{D}}_i^{-1}{\tilde{A}}_i^{(l)}XW\right)$$
从上式可知，$Z$包含了来自$C$个不同meta-path图的节点表示，然后将其应用于下游的分类任务。

五.实验部分

作者采用三个异配数据集来进行实验，数据集的统计特征如下表所示：

---

实验一：节点分类实验

结论：

• 从GTN的性能比所有的baseline要好可以看出，GTN学得的新图结构包含用于学习更有效节点表示的有用meta-path。此外，与baseline中具有常数的简单meta-path邻接矩阵相比，GTN能为边分配可变权重。
• 在表2中${\text{GTN}}_{-I}$表示候选邻接矩阵中没有$I$，从结果可以看出其性能比包含$I$的要差，证明了添加单位阵的有效性。

---

实验二：GTN的解释实验

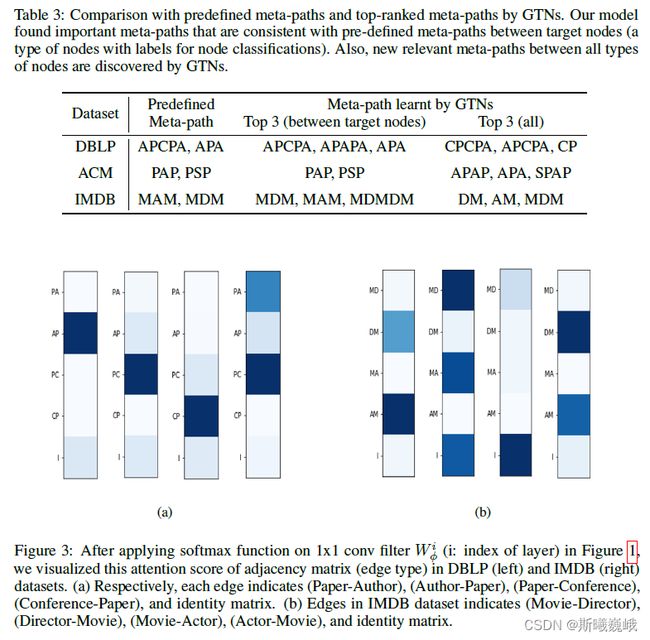
作者经过公式推导得出，一条meta-path $t_l,t_{l-1},...,t_0$的贡献度能通过${\prod }_{i=0}^l{\alpha }_{t_i}^{(i)}$​进行获取，它表明了meta-path在预测任务上的重要程度。表3展示了文献中广泛使用的预定义meta-paths，以及GTN学习的具有高注意力分数的meta-paths。

结论：

• 从表3可以看出，通过领域知识预定义的meta-paths与GTN中学得的排名靠前的meta-paths一致。这表明GTN能学习任务meta-path的重要性。此外，GTN还挖掘了不包含在预定义meta-path集的meta-paths。
• 图3展示了每个GT层的邻接矩阵的注意力分数，(a)为DBLP，(b)为IMDB。与DBLP相比，单位阵在IMDB中有更高的注意力分数。通过给单位阵分配更高的注意力分数，GTN试图坚持更短的meta-paths，即使在更深的层。这表明GTN更根据数据集自适应学习最有效的meta-path的能力。