2022-03-08每日刷题打卡

2022-03-08每日刷题打卡

力扣——每日一题

2055. 蜡烛之间的盘子

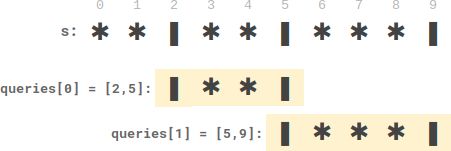
给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 ‘’ 和 ‘|’ ，其中 '’ 表示一个 盘子 ，’|’ 表示一支 蜡烛 。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [lefti, righti] 表示 子字符串 s[lefti…righti] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的 数目 。如果一个盘子在 子字符串中 左边和右边 都 至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

比方说，s = “|||||" ，查询 [3, 8] ，表示的是子字符串 "||**|” 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边 都 至少有一支蜡烛。
请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

输入：s = “||***|”, queries = [[2,5],[5,9]]
输出：[2,3]
解释：

• queries[0] 有两个盘子在蜡烛之间。
• queries[1] 有三个盘子在蜡烛之间。

要找所给区间内蜡烛的数量，我们就要知道所给区间内盘子的出现情况，如果区间左侧有多个盘子挨在一起，我们只看最右的那个蜡烛的下标，如果区间右侧有多个盘子挨在一起，我们只看最左边的那个蜡烛，那么盘子数量就是这俩蜡烛为端点的前缀和。

准备四个数组，一个l记录从左往右出现的蜡烛，一个r记录从右往左出现的蜡烛，一个sum记录盘子数量的前缀和，一个v用来存答案。

先记录盘子数量的前缀和，然后我们从左往右记录蜡烛的出现情况，因为一开始最左边端点不一定是蜡烛，所以我们拿一个变量x=-1,来说明最左边没有蜡烛，开始遍历的时候，如果没遇到蜡烛，就把l数组里走过的地方都变为x，如果遇到了蜡烛，就把蜡烛的下标赋给x，然后把之后走过的位置都赋为x。从右往左也是如此，只不过换了个方向。（蜡烛没出现前的变量不一定是-1，这只是个标记，如果询问的时候，左端点或右端点落在的位置的值是-1的话，说明左边或右边没有蜡烛，那就兜不住这些盘子，此次询问答案是0。不过要注意，左端点我们看的是r数组里蜡烛的情况，右端点是l数组里蜡烛的情况，因为只有区间里两边都有蜡烛才能给盘子计数，所以我们在左端点处要去看右边有没有出现蜡烛，即r[左端点]是否是-1，对于右端点也是一样的，只不过要在l数组里看），举个例子：“* * ||** || * |*”

l数组就是-1 -1 2 3 3 3 6 7 7 9 9

r数组就是2 2 2 3 6 6 6 7 8 8 -1

此时询问【1，5】，我们可以知道，r[1]！=-1,说明右端点有盘子，l[5]!=-1，说明左端点有盘子，那么盘子数就是 l[5]~r[1] 的前缀和。不过还有一个特殊情况，就是[4,5],次数r[4]=6,l[5]=3，这说明了，右边盘子出来的比左盘子早，这显然不和规矩，所以这里也是没盘子的。

class Solution {
public:
    
    vector platesBetweenCandles(string s, vector>& queries) {
        int n=s.size();
        int ans=0;
        vectorv,l(n),r(n),sum(n);
        for(int i=0;i=0;i--)
        {
            if(s[i]=='|')x=i;
            r[i]=x;
        }
        for(auto i:queries)
        {
            int x=r[i[0]],y=l[i[1]];
            v.push_back(x==-1||y==-1||x>=y?0:sum[y]-sum[x]);
        }
        return v;
    }
};

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

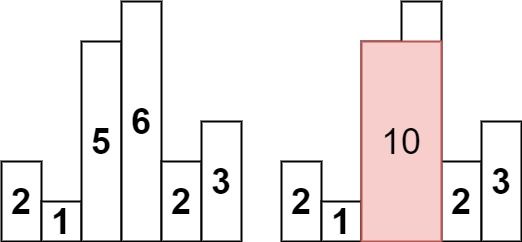
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

0

这题可能有点啰嗦，但看完保证会。

这题我们用单调栈的方式来写，栈顶元素是整个栈里高度最高的柱子的下标。我们每次只看当前柱子高度所能达到的面积，不看这个柱子取不同高度所能达到的面积，比如第一个柱子能达到的面积就是2*1=2，至于它把高度变为1能得到的面积1 *6=6，就是高度为1 的柱子所要考虑的，与它无关。

我们准备一个栈sta，一个变量res用来记录面积的最大值。开始遍历高度数组，遍历到一个元素时，如果栈为空，就直接把这个元素入栈（我们存的不是高度是下标，后面算面积的时候我们要根据下标来算宽度，而高度我们可以通过下标从heights获得）。如果栈不为空则要判断元素的情况，当遍历到的元素高度大于等于栈顶元素高度时，也可以直接入栈；如果小于栈顶元素高度，则开始计算面积，是这样的，如果我们遍历到的元素高度大于等于栈顶元素，说明栈顶元素可以往他那个方向延申，比如下标为1的柱子高度是1，如果当前遍历到的柱子高度是5，那么1当然可以往右边延申，所以直接入栈即可，但如果栈顶元素是高度为6的柱子，那么当下一个元素为2时，他就不能向右边延申了，所以只能开始算高度为6的面积了。面积的算法是宽*高，高就是当前栈顶元素的高度，宽则要考虑情况，我们先把栈顶元素记录下来并出栈，如果此时栈里还有元素，说明这个元素的高度是小于等于之前栈顶元素的，因为小于，所以高度为6也是无法向左扩展的，宽度就是（遍历到的元素的下标-出栈后栈顶元素-1），那么面积就是宽度 *高度了，我们顺便用res记录一下最大值。

此时可能会有疑问，如果栈顶元素是等于之前栈顶元素怎么办，那之前的栈顶元素是可以向左再延申一位的啊。别急我们继续看，当我们通过上面步骤算完了原栈顶元素的面积后，并没有结束，而是要继续去比较，毕竟新的栈顶元素仍然可能比我们遍历到的元素高，如果高，那么我们重复如上操作继续计算出栈并计算栈顶元素面积，直到栈顶元素高度小于等于我们当前元素为止。如果新的栈顶元素是等于之前栈顶元素的话，那么宽度也是（遍历到的元素的下标-出栈后栈顶元素-1），假设下标2 3的元素都是高度为6，到下标4时元素高度小于6了，我们第一个栈顶弹出来时，面积是6*（4-2-1）=6，但当我们下一个高度为6的柱子出来时，面积就是6 *（4-1-1）=12，最大面积并没有变，我们仍然是向右延申的，所以哪怕是相等，这个高度所能获得的最大面积依然不变。以上这些是算面积的一个情况，即出栈后栈顶仍有元素，那么宽度就是（遍历到的元素的下标-出栈后栈顶元素-1），但如果出栈后栈空了，没有栈顶元素，这就说明了，我们最后一个栈顶元素它是之前遍历过的元素里最小的了，那么它的宽度就是之前我们遍历过的所有元素的数量。我们就按照以上步骤遍历高度数组。当我们遍历完高度数组后，如果栈内还有元素，就依次弹出计算面积，此时栈内的所有元素都是可以无限向右延申的，因为右边没有比他们小的柱子了（如果有比他们小的那之前遍历的时候这个元素就会被弹出去了），左边界就是出栈后栈顶元素的下标，那么宽度就是（数组长度-出栈后栈顶元素下标-1） *出栈前栈顶元素高度。如果最后一个元素出栈后栈空了，那这个元素就是整个高度数组里最小的元素了，它的宽度就是数组长度）。

class Solution {
public:
    int largestRectangleArea(vector& heights) {
        stacksta;
        int n = heights.size(), res = 0;
        for (int i = 0; i < n; i++)
        {
            if (sta.empty() || heights[sta.top()] <= heights[i])
                sta.push(i);
            else if (heights[sta.top()] > heights[i])
            {
                while (!sta.empty()&&heights[sta.top()] > heights[i])
                {
                    int ans = sta.top();
                    sta.pop();
                    if (sta.empty())res = max(res, heights[ans] * (i));
                    else res = max(res, heights[ans] * (i - sta.top() - 1));
                }
                sta.push(i);
            }
        }
        while (!sta.empty())
        {
            int ans = sta.top();
            sta.pop();
            if (sta.empty())res = max(res, n * heights[ans]);
            else res = max(res, (n - sta.top()-1) * heights[ans]);
        }
        return res;
    }
};

代码源——每日一题

加一 - 题目 - Daimayuan Online Judge

给定一个整数 n。你需要对它做 m 次操作。在一次操作中，你要将这个数的每一位 d 替换成 d+1。比如，1912 在进行一次操作后将变成 21023。

请求出整数 n 进行了 m 次操作后的长度。答案可能很大，输出对 10^9+7 取模后的结果。

输入格式

第一行一个整数 t，表示测试单元的个数。

接下来 t 行，每行有两个整数 n 和 m，表示最初的数字和进行多少次操作。

输出格式

对于每个测试单元输出最终数字的长度，答案对 10^9+7 取模。

样例输入

5
1912 1
5 6
999 1
88 2
12 100

样例输出

5
2
6
4
2115

数据规模

所有数据保证 1≤t≤2⋅10^{5，1≤n≤10}9，1≤m≤2⋅10^5。

动态规划来接，我们设定状态数组f[N] [10],N是m的上限：2*10^5，10是0~9，f[i] [j]的意思是：原本是j的数位经过i次操作后变成了f[i] [j]位。比如f[1] [9],就是原本这个位置上是9，经过了1次操作后，变成了10，即两位数。

状态转移方程有两种情况，j=0~8是:f[i] [j-1]=f[i-1] [j]; j=9时是f[i] [9]=(f[i-1] [0]+f[i-1] [1])%MOD。因为9加完后是10，位数就是1和0加起来。其余则和+1前的数一样。最后我们以字符串形式读入数字,以数字形式读入操作次数m，然后根据数字每位上的数，将f[m] [j]累加起来即可，注意要取模。

（这题万万没想到会卡输入输出，我超时了半天还不知道为啥。。）

#include
#include
using namespace std;
#include
#include
#include
#include
#include
#include
#include