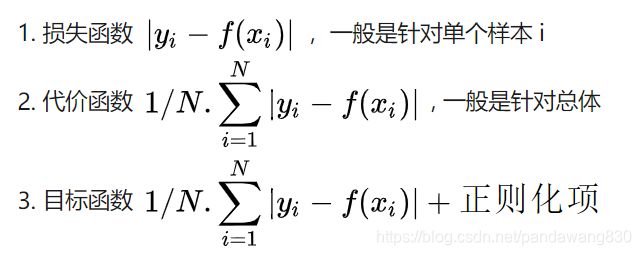线性回归算法梳理
目录
1、机器学习基本概念
2、线性回归原理
3、优化方法
4、线性回归的评估指标
5、sklearn参数详解
1、机器学习基本概念
监督学习:KNN、线性回归、逻辑回归、SVM、决策树和随机森林、神经网络
无监督学习:K-means、聚类分析、可视化和降维-PCA、关联性规则学习
泛化能力:Generalization Ability,是指指机器学习算法对新鲜样本的适应能力。学习的目的是学到隐含在数据背后的规律,对具有同一规律的学习集以外的数据,经过训练的网络也能给出合适的输出,该能力称为泛化能力。
过拟合:把不该学的噪声的特征也学到了,在后期测试的时候不能很好地识别数据,模型泛化能力差。
随着模型训练的进行,模型的复杂度会增加,此时模型在训练数据集上的训练误差会逐渐减小,但是在模型的复杂度达到一定程度时,模型在验证集上的误差反而随着模型的复杂度增加而增大。此时便发生了过拟合,即模型的复杂度升高,但是该模型在除训练集之外的数据集上却不work。
解决方法如:Early Stopping、数据集扩增(Data augmentation)、正则化(Regularization)、Dropout等。
Early Stoopping:记录到目前为止最好的validation accuracy,当连续10次Epoch(或者更多次)没达到最佳accuracy时,则可以认为accuracy不再提高了。此时便可以停止迭代了(Early Stopping)。
数据集扩增:从数据源头采集更多数据;复制原有数据并加上随机噪声;重采样;根据当前数据集估计数据分布参数,使用该分布产生更多数据等。
正则化:L1和L2正则:降低模型复杂度
-L0范数是指向量中非0的元素的个数。
-L1范数是指向量中各个元素绝对值之和,也叫“稀疏规则算子”(Lasso Regularization)。两者都可以实现稀疏性,既然L0可以实现稀疏,为什么不用L0,而要用L1呢?个人理解一是因为L0范数很难优化求解(NP难问题),二是L1范数是L0范数的最优凸近似,而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。
-L2范数是指向量各元素的平方和然后求平方根。可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0。L2正则项起到使得参数w变小加剧的效果,但是为什么可以防止过拟合呢?一个通俗的理解便是:更小的参数值w意味着模型的复杂度更低,对训练数据的拟合刚刚好(奥卡姆剃刀),不会过分拟合训练数据,从而使得不会过拟合,以提高模型的泛化能力。
欠拟合:没有很好地捕捉数据的特征,不能很好的拟合数据
解决方法:
-添加其他特征项,有时候我们模型出现欠拟合的时候是因为特征项不够导致的,可以添加其他特征项来很好地解决。例如,“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段,无论在什么场景,都可以照葫芦画瓢,总会得到意想不到的效果。除上面的特征之外,“上下文特征”、“平台特征”等等,都可以作为特征添加的首选项。
-添加多项式特征,这个在机器学习算法里面用的很普遍,例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。例如上面的图片的例子。
-减少正则化参数,正则化的目的是用来防止过拟合的,但是现在模型出现了欠拟合,则需要减少正则化参数。
偏差和方差:
-准:bias描述的是样本拟合输出的预测结果的期望和真实结果的差距,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就得复杂化模型,增加模型的参数,但容易过拟合,过拟合对应的是high variance,点很分散。low bias对应的是点都在靶心附近,所以瞄点心是准的,但手不一定稳。
-确:variance是样本训练出来的模型在测试集上的表现,想要low variance,需要简单化模型,但是容易欠拟合。欠拟合有high bias,点偏离中心。
交叉验证:Cross Validation
主要用于建模应用中,例如PCR 、PLS 回归建模中。在给定的建模样本中,拿出大部分样本进行建模型,留小部分样本用刚建立的模型进行预报,并求这小部分样本的预报误差,记录它们的平方和。常见形式有Holdout 验证(随机从最初的样本中选出部分,形成交叉验证数据,而剩余的做训练数据),K-fold Cross-validation(初始采样分割成K个子样本,一个单独的子样本被保留作为验证模型的数据,其他K-1个样本用来训练),留一验证(指只使用原本样本中的一项来当做验证资料,而剩余的则留下来当做训练资料)。
2、线性回归原理
线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
代价函数:建模误差的平方和
3、优化方法
梯度下降:
用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数J(θ0,θ1) 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合θ0,θ1,......,θn ,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值,因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值,选择不同的初始参数组合,可能会找到不同的局部最小值。
牛顿法:
牛顿法的基本思想是利用迭代点处的一阶导数 (梯度)和二阶导数 ( Hessen 矩阵) 对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。牛顿法最突出的优点是收敛速度快,具有局部二阶收敛性。
拟牛顿法:
牛顿法是典型的二阶方法,其迭代次数远远小于最值下降法,但是牛顿优化法使用了二阶导数∇2f(x)∇2f(x),在每轮迭代中涉及海森矩阵的求逆,计算复杂度相当高,尤其在高维问题中几乎不可行。若能以较低的计算代价寻求海森矩阵的近似逆矩阵,则可以显著降低计算的时间,这就是拟牛顿法。常用的拟牛顿法有DFP、BFGS、SR1方法等。
4、线性回归的评估指标
RMSE
- Root Mean Square Error,均方根误差
- 是观测值与真值偏差的平方和与观测次数m比值的平方根。
- 是用来衡量观测值同真值之间的偏差
MAE
- Mean Absolute Error ,平均绝对误差
- 是绝对误差的平均值
- 能更好地反映预测值误差的实际情况.
标准差
- Standard Deviation ,标准差
- 是方差的算数平方根
- 是用来衡量一组数自身的离散程度
R-Squared 越大越好
5、sklearn参数详解
sklearn.linear_model提供了很多线性模型,包括岭回归、贝叶斯回归、Lasso等。主要讲解岭回归Ridge的参数。
让我们先看下Ridge这个函数,一共有8个参数:
参数说明如下:
alpha:正则化系数,float类型,默认为1.0。正则化改善了问题的条件并减少了估计的方差。较大的值指定较强的正则化。
fit_intercept:是否需要截距,bool类型,默认为True。也就是是否求解b。
normalize:是否先进行归一化,bool类型,默认为False。如果为真,则回归X将在回归之前被归一化。 当fit_intercept设置为False时,将忽略此参数。 当回归量归一化时,注意到这使得超参数学习更加鲁棒,并且几乎不依赖于样本的数量。 相同的属性对标准化数据无效。然而,如果你想标准化,请在调用normalize = False训练估计器之前,使用preprocessing.StandardScaler处理数据。
copy_X:是否复制X数组,bool类型,默认为True,如果为True,将复制X数组; 否则,它覆盖原数组X。
max_iter:最大的迭代次数,int类型,默认为None,最大的迭代次数,对于sparse_cg和lsqr而言,默认次数取决于scipy.sparse.linalg,对于sag而言,则默认为1000次。
tol:精度,float类型,默认为0.001。就是解的精度。
solver:求解方法,str类型,默认为auto。可选参数为:auto、svd、cholesky、lsqr、sparse_cg、sag。
auto根据数据类型自动选择求解器。
svd使用X的奇异值分解来计算Ridge系数。对于奇异矩阵比cholesky更稳定。
cholesky使用标准的scipy.linalg.solve函数来获得闭合形式的解。
sparse_cg使用在scipy.sparse.linalg.cg中找到的共轭梯度求解器。作为迭代算法,这个求解器比大规模数据(设置tol和max_iter的可能性)的cholesky更合适。
lsqr使用专用的正则化最小二乘常数scipy.sparse.linalg.lsqr。它是最快的,但可能在旧的scipy版本不可用。它是使用迭代过程。
sag使用随机平均梯度下降。它也使用迭代过程,并且当n_samples和n_feature都很大时,通常比其他求解器更快。注意,sag快速收敛仅在具有近似相同尺度的特征上被保证。您可以使用sklearn.preprocessing的缩放器预处理数据。
random_state:sag的伪随机种子。