二维数组的总结

一、时间复杂度和空间复杂度

  时间复杂度和空间复杂度是衡量算法效率的两个重要指标。时间复杂度是指算法执行所需的时间，而空间复杂度是指算法执行所需的内存空间。

  计算时间复杂度和空间复杂度需要分析算法中各个操作的执行次数和内存使用情况。具体的计算方法可以根据算法的具体实现来确定，但一般情况下可以采用以下步骤：
（1）确定算法的基本操作：对于一个算法，我们需要先确定其基本操作，即算法的基本执行单元，例如赋值操作、比较操作、循环操作等。
（2）分析算法的执行次数：对于每个基本操作，我们需要分析其在算法中的执行次数，然后将这些操作的执行次数相加，得到算法的总执行次数。通常使用大O符号表示算法的时间复杂度。
（3）评估算法的空间复杂度：对于算法的内存使用情况，我们需要分析算法中所使用的数据结构、变量和递归等情况，然后评估算法的空间复杂度。同样也可以使用大O符号表示算法的空间复杂度。

二、二维数组简介

  二维数组是一种结构较为特殊的数组，只是将数组中的每个元素变成了一维数组。所以二维数组的本质上仍然是一个一维数组，内部的一维数组仍然从索引 0 开始，我们可以将它看作一个矩阵，并处理矩阵的相关问题。

  注意，实际数组中的元素由于类型的不同会占用不同的字节数，因此每个方格地址之间的差值可能不为 1。实际题目中，往往使用二维数组处理矩阵类相关问题，包括矩阵旋转、对角线遍历，以及对子矩阵的操作等。

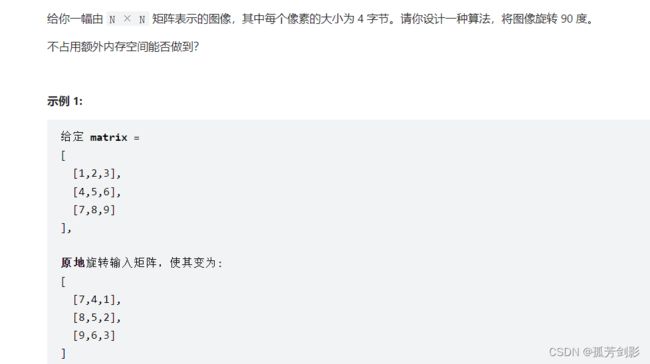
三、旋转矩阵

解法1：使用辅助数组

c

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
    int matrix_new[matrixSize][matrixSize];
    for (int i = 0; i < matrixSize; i++) {
        for (int j = 0; j < matrixSize; j++) {
            matrix_new[i][j] = matrix[i][j];
        }
    }
    for (int i = 0; i < matrixSize; ++i) {
        for (int j = 0; j < matrixSize; ++j) {
            matrix[j][matrixSize - i - 1] = matrix_new[i][j];
        }
    }
}

c++

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // C++ 这里的 = 拷贝是值拷贝，会得到一个新的数组
        auto matrix_new = matrix;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                matrix_new[j][n - i - 1] = matrix[i][j];
            }
        }
        // 这里也是值拷贝
        matrix = matrix_new;
    }
};

解法2：原地旋转

c:

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
    for (int i = 0; i < matrixSize / 2; ++i) {
        for (int j = 0; j < (matrixSize + 1) / 2; ++j) {
            int temp = matrix[i][j];
            matrix[i][j] = matrix[matrixSize - j - 1][i];
            matrix[matrixSize - j - 1][i] = matrix[matrixSize - i - 1][matrixSize - j - 1];
            matrix[matrixSize - i - 1][matrixSize - j - 1] = matrix[j][matrixSize - i - 1];
            matrix[j][matrixSize - i - 1] = temp;
        }
    }
}

c++

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};

解法3：用翻转代替旋转

c

void swap(int* a, int* b) {
    int t = *a;
    *a = *b, *b = t;
}

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
    // 水平翻转
    for (int i = 0; i < matrixSize / 2; ++i) {
        for (int j = 0; j < matrixSize; ++j) {
            swap(&matrix[i][j], &matrix[matrixSize - i - 1][j]);
        }
    }
    // 主对角线翻转
    for (int i = 0; i < matrixSize; ++i) {
        for (int j = 0; j < i; ++j) {
            swap(&matrix[i][j], &matrix[j][i]);
        }
    }
}

c++

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};