单晶塑性abaqus-umat自学

本文以翻译黄永刚老师的umat文章为主， 这个颜色的为补充材料和个人的理解。

摘要

包含单晶塑性的abaqus用户材料子程序。本文回顾有限元形式的单晶弹塑性和黏弹塑性，包含小变形理论，以及严格的有限变形和有限旋转理论。单晶的非弹性变形由于晶体滑移，假定遵从Schmid准则。提出多种多样的分切应力与剪切变形的自硬化和潜硬化关系，并且包含在子程序内。

1. 简介

  有限元程序ABAQUS已经广泛应用在固体的变形与应力分析。除了自身大量的本构模型，ABAQUS还提供用户子程序接口。应力、应变以及求解依赖的状态变量以增量形式求出。当umat子程序被访问时，提供增量步开始的状态（应力以及求解依赖的状态变量）和应变和时间增量。umat子程序执行二段程序：更新应力和状态变量使其等于增量步结束时对应的值，提供材料的Jacobian矩阵，$\partial \Delta \sigma /\partial \Delta \epsilon$，为Newton-Rhapson迭代提供相应的本构模型。

  本文的主要目标是提供单晶塑性的本构的框架。运动学部分严格满足有限变形。塑性变形仅仅考虑位错滑移，不考虑扩散变形，孪晶和晶界滑移。Schmid应力，或滑移系上分切应力假定是滑移的驱动力。完整的子程序用于单晶和双晶的变形和断裂分析。

2. 单晶弹塑性本构模型回顾

2.1运动学

  晶体力学的运动学理论的先驱是Taylor（1938），精准的力学理论是Hill（1966），Rice（1971）和Hill and Rice（1972）搭建的。下面是关于Asaro and Rice（1977）和Asaro（1983）简单的理论总结。
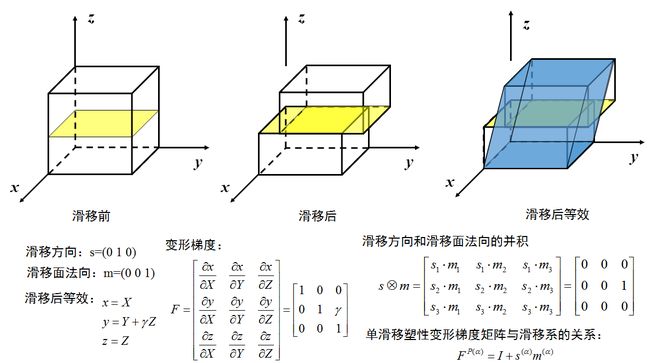
  晶体材料的弹性变形和旋转是由晶格承担的。单晶的非弹性变形源于晶体滑移。材料流动是通过位错在晶格上的运动。总的变形梯度$\mathbf{F}$:$$\mathbf{F}={\mathbf{F}}^{\ast }\cdot {\mathbf{F}}^{\mathbf{P}}$$
  其中 $F^P$ 是中间构型的塑性剪切，$F^{\ast }$ 为晶格拉伸和旋转。假设弹性特征不受滑移的影响，应力由$F^{\ast }$ 单独决定。$F^P$ 的变化率与 $\alpha$ 滑移系的滑移率 ${\dot{\gamma }}^{(\alpha )}$ 有关。
$$\dot{{\mathbf{F}}^P}\cdot \dot{{\mathbf{F}}^{P-1}}=\sum _{\alpha }{\dot{\gamma }}^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}$$
  对所有激活的滑移系求和，$s^{(\alpha )}$ 和 $m^{(\alpha )}$ 分别是参考构型下滑移方向和滑移面的法向。

---

补充：单滑移变形梯度描述

速度梯度张量 $\mathbf{L}$
$$\begin{array}{rl}\mathbf{L}& =\dot{\mathbf{F}}\cdot {\mathbf{F}}^{-1}={\dot{\mathbf{F}}}^{\ast }\cdot {\mathbf{F}}^{\mathbf{P}}\cdot {\mathbf{F}}^{\mathbf{P}-1}\cdot {\mathbf{F}}^{\ast -1}+{\mathbf{F}}^{\ast }\cdot {\dot{\mathbf{F}}}^{\mathbf{P}}\cdot {\mathbf{F}}^{\mathbf{P}-1}\cdot {\mathbf{F}}^{\ast -1}\\ & ={\dot{\mathbf{F}}}^{\ast }\cdot {\mathbf{F}}^{\ast -1}+{\mathbf{F}}^{\ast }\cdot {\dot{\mathbf{F}}}^{\mathbf{P}}\cdot {\mathbf{F}}^{\mathbf{P}-1}\cdot {\mathbf{F}}^{\ast -1}\end{array}$$
求 ${\mathbf{F}}^{\mathbf{P}-1}$ 由于：
$$\begin{array}{rl}& [\mathbf{I}-{\gamma }^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}]\cdot [\mathbf{I}+{\gamma }^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}]\\ & \\ =& \mathbf{I}-{\gamma }^{(\alpha {)}^2}{s}^{(\alpha )}{m}^{(\alpha )}\cdot s^{(\alpha )}{m}^{(\alpha )}\end{array}$$
滑移方向和滑移面法向垂直：$m^{(\alpha )}\cdot s^{(\alpha )}=0$

因此： $${\mathbf{F}}^{\mathbf{P}-1}=\mathbf{I}-{\gamma }^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}$$
$$\dot{{\mathbf{F}}^{\mathbf{P}}}\cdot {\mathbf{F}}^{\mathbf{P}-1}=[{\dot{\gamma }}^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}]\cdot [\mathbf{I}-{\gamma }^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}]={\dot{\gamma }}^{(\alpha )}{s}^{(\alpha )}{m}^{(\alpha )}$$

---

  为了方便定义$s^{\ast (\alpha )}$ 为 $\alpha$ 滑移系在变形后的构型中的滑移方向：
$$s^{\ast (\alpha )}=F^{\ast }\cdot s^{(\alpha )}$$
  定义$m^{\ast (\alpha )}$ 为 $\alpha$ 滑移系在变形后的构型中的滑移面的法向：
$$m^{\ast (\alpha )}=m^{(\alpha )}\cdot F^{\ast -1}$$

---

因此：
$$\begin{array}{rl}\mathbf{L}& ={\dot{\mathbf{F}}}^{\ast }\cdot {\mathbf{F}}^{\ast -1}+{\dot{\gamma }}^{(\alpha )}{\mathbf{F}}^{\ast }\cdot s^{(\alpha )}{m}^{(\alpha )}\cdot {\mathbf{F}}^{\ast -1}\\ & \\ & ={\dot{\mathbf{F}}}^{\ast }\cdot {\mathbf{F}}^{\ast -1}+{\dot{\gamma }}^{(\alpha )}{\mathbf{s}}^{\ast (\alpha )}{\mathbf{m}}^{\ast (\alpha )}\\ & \\ & ={\mathbf{L}}^{\ast }+{\mathbf{L}}^{\mathbf{P}}\end{array}$$

---

  当前状态的速度梯度矩阵：
$$\mathbf{L}=\dot{\mathbf{F}}\cdot {\mathbf{F}}^{-1}=\mathbf{D}+\mathbf{\Omega }$$
  其中，$D$ 为对称的拉伸率，$\Omega$ 为反对称的自旋张量。可分解为晶格部分（上标*）和塑性部分（上标P）：
$$\mathbf{D}={\mathbf{D}}^{\ast }+{\mathbf{D}}^{\mathbf{P}}\mathbf{\Omega }={\mathbf{\Omega }}^{\ast }+{\mathbf{\Omega }}^{\mathbf{P}}$$
  满足：$${\mathbf{D}}^{\ast }+{\mathbf{\Omega }}^{\ast }={\dot{\mathbf{F}}}^{\ast }\cdot {\mathbf{F}}^{\ast -1}{\mathbf{D}}^{\mathbf{P}}+{\mathbf{\Omega }}^{\mathbf{P}}=\sum _{\alpha }{\dot{\gamma }}^{(\alpha )}{\mathbf{s}}^{\ast (\alpha )}{\mathbf{m}}^{\ast (\alpha )}$$

2.2 本构

  依据 Hill and Rice（1972），存在弹性势能，$\Phi =\Phi (F^{\ast })$ ，保证对称的晶格变形率张量 ${\mathbf{D}}^{\ast }$, 和Cauchy应力的Jaumann客观应变率满足如下关系：
$${\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)=\mathbf{L}:{\mathbf{D}}^{\ast }\text{\hspace{1em}(2.2.1)}$$
其中$I$是二阶单位张量，$\mathbf{L}$ 是弹性张量具有如下对称性$L_{ijkl}=L_{jikl}=L_{ijlk}=L_{klij}$，Jaumann率 ${\stackrel{\nabla }{\sigma }}^{\ast }$ 是晶格坐标轴上的共转应力率，Jaumann率 $\stackrel{\nabla }{\sigma }$ 是材料坐标轴上的共转应力率，二者之间的关系：
$${\stackrel{\nabla }{\sigma }}^{\ast }=\stackrel{\nabla }{\sigma }+(\Omega -{\Omega }^{\ast })\cdot \sigma -\sigma \cdot (\Omega -{\Omega }^{\ast })\text{\hspace{1em}(2.2.2)}$$
其中，$\stackrel{\nabla }{\sigma }=\dot{\mathbf{\sigma }}-\Omega \cdot \sigma +\sigma \cdot \Omega$

---

补充：

在Lagrange坐标下，变形率 $D^{\ast }$ 和 Kirchhoff应力 ${\tau }^{\ast }=J{\sigma }^{\ast }$ 共轭
$${\stackrel{\nabla }{\tau }}^{\ast }=\mathbf{L}:{\mathbf{D}}^{\ast }$$
其中：
$$\begin{array}{rl}{\stackrel{\nabla }{\tau }}^{\ast }& =\dot{{\tau }^{\ast }}-\Omega \cdot {\tau }^{\ast }+{\tau }^{\ast }\cdot \Omega \\ & =\dot{J}{\sigma }^{\ast }+J\dot{{\sigma }^{\ast }}-J\Omega \cdot {\sigma }^{\ast }+J{\sigma }^{\ast }\cdot \Omega \\ & =J{\sigma }^{\ast }(I:D)+J\dot{{\sigma }^{\ast }}-J\Omega \cdot {\sigma }^{\ast }+J{\sigma }^{\ast }\cdot \Omega \\ & =J\left[{\sigma }^{\ast }(I:D)+\stackrel{\nabla }{{\sigma }^{\ast }}\right]\end{array}$$
考虑到从初始构型到中间构型只发生滑移，忽略体积变化$J=\det F\approx 1$
因此：
$${\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)=\mathbf{L}:{\mathbf{D}}^{\ast }$$

---

  晶体滑移遵循Schmid准则，任意滑移系 $\alpha$的滑移率 ${\dot{\gamma }}^{(\alpha )}$假设只与当前应力 $\sigma$ 的Schmid应力 ${\tau }^{(\alpha )}$。Schmid应力是忽略晶格畸变后的分切应力。Asaro and Rice（1977）讨论了现有有限弹性畸变的一些可能的一般化。本文基于Rice（1971），热力学应力与滑移共轭。定义：
$${\tau }^{(\alpha )}=m^{\ast (\alpha )}\cdot \frac{{\rho }_0}{\rho }\sigma \cdot s^{\ast (\alpha )}\text{\hspace{1em}(2.2.3)}$$
其中 ${\rho }_0$ 和 $\rho$ 参考构型和当前构型的密度；Hill and Rice(1972)认为${\tau }^{(\alpha )}$等于随晶格旋转的Kirchhoff应力的最大剪切分量。Schmid应力的变化率如下：
$${\dot{\tau }}^{(\alpha )}=m^{\ast (\alpha )}\cdot \left[{\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)-{\mathbf{D}}^{\ast }\cdot \mathbf{\sigma }+\mathbf{\sigma }\cdot {\mathbf{D}}^{\ast }\right]\cdot s^{\ast (\alpha )}\text{\hspace{1em}(2.2.4)}$$

---

补充：

式（2.2.3）中：$$\frac{{\rho }_0}{\rho }=\frac{dv}{dV}=J$$
因此：
$${\dot{\tau }}^{(\alpha )}={\dot{m}}^{\ast (\alpha )}\cdot J\sigma \cdot s^{\ast (\alpha )}+m^{\ast (\alpha )}\cdot \dot{(J\sigma )}\cdot s^{\ast (\alpha )}+m^{\ast (\alpha )}\cdot J\sigma \cdot {\dot{s}}^{\ast (\alpha )}$$
其中：
$$\begin{array}{rl}{m}^{\ast (\alpha )}\cdot \dot{(J\sigma )}\cdot s^{\ast (\alpha )}& =m^{\ast (\alpha )}\cdot [\stackrel{\nabla }{(J\sigma )}+{\Omega }^{\ast }\cdot \sigma -\sigma \cdot {\Omega }^{\ast }]\cdot s^{\ast (\alpha )}\\ & =m^{\ast (\alpha )}\cdot [{\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)-{\Omega }^{\ast }\cdot \sigma +\sigma \cdot {\Omega }^{\ast }]\cdot s^{\ast (\alpha )}\end{array}$$
忽略体积变化$J=\det F\approx 1$
$$\begin{array}{rl}{\dot{m}}^{\ast (\alpha )}\cdot \sigma \cdot s^{\ast (\alpha )}& =m^{(\alpha )}\cdot {\dot{F}}^{\ast -1}\cdot \sigma \cdot s^{\ast (\alpha )}\\ & =m^{\ast (\alpha )}\cdot F^{\ast }\cdot {\dot{F}}^{\ast -1}\cdot \sigma \cdot s^{\ast (\alpha )}\\ & =m^{\ast (\alpha )}\cdot -L^{\ast }\cdot \sigma \cdot s^{\ast (\alpha )}\end{array}$$
注：$$\dot{\mathbf{I}}=\dot{({\mathbf{F}}^{\ast }\cdot {\mathbf{F}}^{\ast -1})}=\dot{{\mathbf{F}}^{\ast }}\cdot {\mathbf{F}}^{\ast -1}+{\mathbf{F}}^{\ast }\cdot {\dot{\mathbf{F}}}^{\ast -1}=0$$
其中：$\dot{{\mathbf{F}}^{\ast }}\cdot {\mathbf{F}}^{\ast -1}={\mathbf{L}}^{\ast }$ ,因此${\mathbf{F}}^{\ast }\cdot {\dot{\mathbf{F}}}^{\ast -1}=-{\mathbf{L}}^{\ast }$
同理：
$$\begin{array}{rl}{m}^{\ast (\alpha )}\cdot \sigma \cdot {\dot{s}}^{\ast (\alpha )}& =m^{(\ast \alpha )}\cdot \sigma \cdot \dot{F^{\ast }}\cdot s^{(\alpha )}\\ & =m^{\ast (\alpha )}\cdot \sigma \cdot \dot{F^{\ast }}\cdot F^{\ast -1}{s}^{\ast (\alpha )}\\ & =m^{\ast (\alpha )}\cdot \sigma \cdot L^{\ast }\cdot s^{\ast (\alpha )}\end{array}$$
因此：
$$\begin{array}{rl}{\dot{\tau }}^{(\alpha )}& ={\dot{m}}^{\ast (\alpha )}\cdot [{\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)+{\Omega }^{\ast }\cdot \sigma -\sigma \cdot {\Omega }^{\ast }-L^{\ast }\cdot \sigma +\sigma \cdot L^{\ast }]\cdot s^{\ast (\alpha )}\\ & ={\dot{m}}^{\ast (\alpha )}\cdot [{\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)-D^{\ast }\cdot \sigma +\sigma \cdot D^{\ast }]\cdot s^{\ast (\alpha )}\end{array}$$

---

2.3 率相关的晶体材料硬化

  率无关的塑性是率相关塑性的极限。基于Schmid准则，$\alpha$ 滑移系的滑移率 ${\dot{\gamma }}^{(\alpha )}$ 依赖于相应的分切应力
$${\dot{\gamma }}^{(\alpha )}={\dot{a}}^{(\alpha )}{f}^{(\alpha )}\left(\frac{{\tau }^{(\alpha )}}{g^{(\alpha )}}\right)\text{\hspace{1em}(2.3.1)}$$
其中，${\dot{a}}^{(\alpha )}$ 为参考应变率， $g^{(\alpha )}$ 是滑移系当前的强度，$f^{(\alpha )}$ 无量纲的描述应力和应变率的函数。Hutchinson（1976）利用简单幂律形式表示多晶蠕变：

$$f^{(\alpha )}(x)=x|x{|}^{n-1}\text{\hspace{1em}(2.3.1a)}$$

其中，$n$ 为率敏感指数，$n\to \infty$ 近似应变率无关。
应变硬化以增量形式给出：
$${\dot{g}}^{(\alpha )}=\sum _{\beta }{h}_{\alpha \beta }{\dot{\gamma }}^{(\beta )}\text{\hspace{1em}(2.3.2)}$$
其中 $h_{\alpha \beta }$ 为滑移的硬化模量，在所有激活的滑移系上求和。$h_{\alpha \alpha }$称为自硬化系数，$h_{\alpha \beta }$ $(\alpha \ne \beta )$ 为潜硬化系数。

 Peirce，Asaro and Needleman（1982）和Asaro（1983a，b）利用简单形式自硬化系数：
$$h_{\alpha \alpha }=h(\gamma )=h_0{\mathrm{sech}}^2\left|\frac{h_0\gamma }{{\tau }_s-{\tau }_0}\right|(\alpha 不求和)\text{\hspace{1em}(2.3.3a)}$$

其中 $h_0$ 为初始硬化模量，${\tau }_0$屈服强度，等于当前强度的初始值 $g^{(\alpha )}(0)$，$\gamma$ 是所有滑移系上的Taylor累计剪切应变：
$$\gamma =\sum _{\alpha }{\int }_0^t\left|{\dot{\gamma }}^{(\alpha )}\right|dt\text{\hspace{1em}(2.3.3b)}$$
潜硬化模量：
$$h_{\alpha \beta }=qh(\gamma )(\alpha \ne \beta )\text{\hspace{1em}(2.3.3c)}$$
$q$ 为常数。这些表达式忽略Bauschinger效应。
 Bassani and Wu(1991)三阶段硬化：
$$h_{\alpha \alpha }=\left\{(h_0-h_s){\mathrm{sech}}^2\left|\frac{(h_0-h_s)\gamma }{{\tau }_s-{\tau }_0}\right|+h_s\right\}G({\gamma }^{(\beta )};\beta \ne \alpha )(\alpha 不求和)\text{\hspace{1em}(2.3.4a)}$$
$$h_{\beta \alpha }=q{h}_{\alpha \alpha }\beta \ne \alpha \text{\hspace{1em}(2.3.4b)}$$
$h_s$ 为易滑移阶段硬化模量，$G$ 是交滑移相关的函数
$$G({\gamma }^{(\beta )};\beta \ne \alpha )=1+\sum _{\beta \ne \alpha }{f}_{\alpha \beta }\tanh \left(\frac{{\gamma }^{(\beta )}}{{\gamma }_0}\right)\text{\hspace{1em}(2.3.4c)}$$
${\gamma }_0$ 是相互作用滑移系的滑移总量，$f_{\alpha \beta }$ 相互作用的强度。例子，共面滑移的相互作用小于非共面滑移。

  上述表达中没有明确的屈服，只要分切应力非零就会发生塑性剪切，然而，对于较大率敏感指数n（n≥50）,当分切应力小于 ${\tau }_0$ 塑性剪切率远远小于参考应变率 $\dot{a}$。 所以激活的滑移系没必要区分$(s^{\ast (\alpha )},m^{\ast (\alpha )})$ 和 $(-s^{\ast (\alpha )},m^{\ast (\alpha )})$，所以当 ${\tau }^{\ast (\alpha )}$为负允许 ${\dot{\gamma }}^{\ast (\alpha )}$取负值。

3. 向前梯度时间积分方案和增量方程

本文两种时间积分方案。第一种方案在应力，应变和状态变量如剪切应变、分切应力、滑移当前的强度增量之间存在线性关系，这种假设在3.1-3.3中。应力和状态变量在时间增量步开始前进行更新。第二种方案是用Newton-Rhapson迭代求解非线性增量方程，详见3.4节。隐式时间积分方案，应力和状态变量在时间增量结束时进行计算。

3.1 向前梯度时间积分方案

 率相关固体的切线模量方法被Peice,Shih and Needleman(1984)用在子程序中。我们定义在时间增量 $\Delta t$ 内 $\alpha$ 滑移系的应变增量为 ${\gamma }^{(\alpha )}$:
$$\Delta {\gamma }^{(\alpha )}={\gamma }^{(\alpha )}(t+\Delta t)-{\gamma }^{(\alpha )}(t)\text{\hspace{1em}(3.1.1)}$$
采用线性差值：
$$\Delta {\gamma }^{(\alpha )}=\Delta t\left[(1-\theta ){\dot{\gamma }}_t^{(\alpha )}+\theta {\dot{\gamma }}_{t+\Delta t}^{(\alpha )}\right]\text{\hspace{1em}(3.1.2)}$$
参数 $\theta$ 取值范围0~1，取0为简单的Euler积分。 $\theta$ 取值建议0.5~1（Peirce et al，1984）。

 滑移率 ${\dot{\gamma }}^{(\alpha )}$ 是分切应力 ${\tau }^{(\alpha )}$ 和当前滑移系强度 $g^{(\alpha )}$的函数。滑移率的Taylor展开:
$${\dot{\gamma }}_{t+\Delta t}^{(\alpha )}={\dot{\gamma }}_t^{(\alpha )}+\frac{\partial {\dot{\gamma }}_t^{(\alpha )}}{\partial {\tau }^{(\alpha )}}\Delta {\tau }^{(\alpha )}++\frac{\partial {\dot{\gamma }}_t^{(\alpha )}}{\partial g^{(\alpha )}}\Delta g^{(\alpha )}\text{\hspace{1em}(3.1.3)}$$
联立(3.1.1)~(3.1.3)给出以下增量表达式：
$$\Delta {\gamma }^{(\alpha )}=\Delta t\left[{\dot{\gamma }}_t^{(\alpha )}+\theta \frac{\partial {\dot{\gamma }}_t^{(\alpha )}}{\partial {\tau }^{(\alpha )}}\Delta {\tau }^{(\alpha )}+\theta \frac{\partial {\dot{\gamma }}_t^{(\alpha )}}{\partial g^{(\alpha )}}\Delta g^{(\alpha )}\right]\text{\hspace{1em}(3.1.4)}$$

3.2 增量表达式

 在这一部分中，已知时间增量为$\Delta t$应变增量为$\Delta {\epsilon }_{ij}$，推导出所有滑移系上滑移应变增量 $\Delta {\gamma }^{(\alpha )}$，分切应力增量$\Delta {\tau }^{(\alpha )}$和当前强度$\Delta g^{(\alpha )}$的关系。共转应力增量$\Delta {\sigma }_{ij}={\stackrel{\nabla }{\sigma }}_{ij}\Delta t$通过应变增量$\Delta {\epsilon }_{ij}$表示。应力增量的更新和有限变形的ABAQUS有限元程序相同。

 为了方便引入每个滑移系的“Schmid因子”${\mu }_{ij}^{(\alpha )}$和张量${\omega }_{ij}^{(\alpha )}$:
$${\mu }_{ij}^{(\alpha )}=\frac{1}{2}\left[s_i^{\ast (\alpha )}{m}_j^{\ast (\alpha )}+s_j^{\ast (\alpha )}{m}_i^{\ast (\alpha )}\right]\text{\hspace{1em}(3.2.1a)}$$
$${\omega }_{ij}^{(\alpha )}=\frac{1}{2}\left[s_i^{\ast (\alpha )}{m}_j^{\ast (\alpha )}-s_j^{\ast (\alpha )}{m}_i^{\ast (\alpha )}\right]\text{\hspace{1em}(3.2.1b)}$$

张量${\omega }_{ij}^{(\alpha )}$和旋转张量$\Omega$和${\Omega }^{\ast }$的关系：
$${\Omega }_{ij}-{\Omega }_{ij}^{\ast }=\sum _{\alpha }{\omega }_{ij}^{(\alpha )}{\dot{\gamma }}^{(\alpha )}\text{\hspace{1em}(3.2.1c)}$$

 通过晶体滑移硬化方程(2.3.2)，得出当前硬化函数增量的表达式如下：
$$\Delta g^{(\alpha )}=\sum _{\beta }{h}_{\alpha \beta }\Delta {\gamma }^{(\beta )}\text{\hspace{1em}(3.2.2)}$$
联立方程（2.2.4），弹性本构（2.2.1）以及将应变增量分解为晶格变形（2.1.4）和塑性变形（2.1.5）得出应变增量$\Delta {\epsilon }_{ij}$与分切应力$\Delta {\tau }^{(\alpha )}$的关系：
$$\Delta {\tau }^{(\alpha )}=\left[L_{ijkl}{\mu }_{kl}^{(\alpha )}+{\omega }_{ik}^{(\alpha )}{\sigma }_{jk}+{\omega }_{jk}^{(\alpha )}{\sigma }_{ik}\right]:\left[\Delta {\epsilon }_{ij}-\sum _{\beta }{\mu }_{ij}^{(\beta )}\Delta {\gamma }^{(\beta )}\right]\text{\hspace{1em}(3.2.3)}$$
其中$L_{ijkl}$是弹性模量矩阵。通过方程（2.2.2）给出共转应力增量$\Delta {\sigma }_{ij}$：
$$\Delta {\sigma }_{ij}=L_{ijkl}\Delta {\epsilon }_{kl}-{\sigma }_{ij}\Delta {\epsilon }_{kk}-\sum _{\alpha }\left[L_{ijkl}{\mu }^{(\alpha )}+{\omega }_{ik}^{(\alpha )}{\sigma }_{jk}+{\omega }_{jk}^{(\alpha )}{\sigma }_{ik}\right]\cdot \Delta {\gamma }^{(\alpha )}\text{\hspace{1em}(3.2.4)}$$

---

补充：(2.2.4)可改写为

$${\dot{\tau }}^{(\alpha )}={\mathbf{m}}^{\ast (\mathbf{\alpha })}{\mathbf{s}}^{\ast (\mathbf{\alpha })}:\left[{\stackrel{\nabla }{\sigma }}^{\ast }+\mathbf{\sigma }\left(\mathbf{I}:{\mathbf{D}}^{\ast }\right)-{\mathbf{D}}^{\ast }\cdot \mathbf{\sigma }+\mathbf{\sigma }\cdot {\mathbf{D}}^{\ast }\right]$$
${\mathbf{m}}^{\ast (\mathbf{\alpha })}{\mathbf{s}}^{\ast (\mathbf{\alpha })}$为向量${\mathbf{m}}^{\ast (\mathbf{\alpha })}$和向量${\mathbf{s}}^{\ast (\mathbf{\alpha })}$的并积，写成分量形式为$m_i^{\ast (\alpha )}{s}_j^{\ast (\alpha )}$。
由（3.2.1）可知：
$$m_i^{\ast (\alpha )}{s}_j^{\ast (\alpha )}={\mu }_{ij}^{(\alpha )}-{\omega }_{ij}^{(\alpha )}$$
代入上式，可得：
$$\begin{array}{rl}{\dot{\tau }}^{(\alpha )}& ={\mathbf{m}}_{\mathbf{i}}^{\ast (\mathbf{\alpha })}{\mathbf{s}}_{\mathbf{j}}^{\ast (\mathbf{\alpha })}:\left[L_{ijkl}:D_{kl}^{\ast }-D_{ik}^{\ast }\cdot {\sigma }_{kj}+{\sigma }_{ik}\cdot D_{kj}^{\ast }\right]\\ & =({\mu }_{ij}^{(\alpha )}-{\omega }_{ij}^{(\alpha )}):\left[L_{ijkl}:D_{kl}^{\ast }-D_{ik}^{\ast }\cdot {\sigma }_{kj}+{\sigma }_{ik}\cdot D_{kj}^{\ast }\right]\end{array}$$
其中：$${\mu }_{ij}^{(\alpha )}:L_{ijkl}:D_{kl}^{\ast }={\mu }_{kl}^{(\alpha )}:L_{klij}:D_{ij}^{\ast }$$
又因为：$L_{ijkl}=L_{klij}$
$${\mu }_{ij}^{(\alpha )}:L_{ijkl}:D_{kl}^{\ast }=(L_{ijkl}:{\mu }_{kl}^{(\alpha )}):D_{ij}^{\ast }$$
其中：$${\omega }_{ij}^{(\alpha )}:L_{ijkl}:D_{kl}^{\ast }={\omega }_{kl}^{(\alpha )}:L_{klij}:D_{ij}^{\ast }$$
又因为：$L_{ijkl}=L_{klij}=L_{ijlk}$且反对称张量${\omega }_{kl}=-{\omega }_{lk}$
$$\begin{array}{rl}{\omega }_{ij}^{(\alpha )}:L_{ijkl}:D_{kl}^{\ast }& =(L_{ijkl}:{\omega }_{kl}^{(\alpha )}):D_{ij}^{\ast }=(L_{ijlk}:{\omega }_{lk}^{(\alpha )}):D_{ij}^{\ast }\\ & =-(L_{ijkl}:{\omega }_{kl}^{(\alpha )}):D_{ij}^{\ast }\end{array}$$
$$(L_{ijkl}:{\omega }_{kl}^{(\alpha )}):D_{ij}^{\ast }=-(L_{ijkl}:{\omega }_{kl}^{(\alpha )}):D_{ij}^{\ast }$$
因此：${\omega }_{ij}^{(\alpha )}:L_{ijkl}:D_{kl}^{\ast }=0$
继续计算共转项：
$$({\mu }_{ij}^{(\alpha )}-{\omega }_{ij}^{(\alpha )}):\left[-D_{ik}^{\ast }\cdot {\sigma }_{kj}+{\sigma }_{ik}\cdot D_{kj}^{\ast }\right]$$
考虑到${\mu }_{ij}^{(\alpha )}{D}_{ik}^{\ast }{\sigma }_{kl}$均为对称常量，考虑对称性可得
$$-{\mu }_{ij}^{(\alpha )}:(D_{ik}^{\ast }\cdot {\sigma }_{kj})=-{\mu }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}:D_{ij}^{\ast }$$
$${\mu }_{ij}^{(\alpha )}:({\sigma }_{ik}\cdot D_{kj}^{\ast })={\mu }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}:D_{ij}^{\ast }$$
$${\mu }_{ij}^{(\alpha )}:\left[-D_{ik}^{\ast }\cdot {\sigma }_{kj}+{\sigma }_{ik}\cdot D_{kj}^{\ast }\right]=0$$
张量${\omega }_{ij}^{(\alpha )}$为反对称张量：
$${\omega }_{ij}^{(\alpha )}:(D_{ik}^{\ast }\cdot {\sigma }_{kj})={\omega }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}:D_{ij}^{\ast }$$
$$-{\omega }_{ij}^{(\alpha )}:({\sigma }_{ik}\cdot D_{kj}^{\ast })=-{\sigma }_{ik}\cdot {\omega }_{kj}^{(\alpha )}:D_{ij}^{\ast }={\omega }_{jk}^{(\alpha )}\cdot {\sigma }_{ik}:D_{ij}^{\ast }$$
$$-{\omega }_{ij}^{(\alpha )}:\left[-D_{ik}^{\ast }\cdot {\sigma }_{kj}+{\sigma }_{ik}\cdot D_{kj}^{\ast }\right]=[{\omega }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}+{\omega }_{jk}^{(\alpha )}\cdot {\sigma }_{ik}]:D_{ij}^{\ast }$$
弹性应变增量=总应变-塑性应变：
$$\begin{array}{rl}\Delta {\epsilon }_{ij}^e& =\Delta {\epsilon }_{ij}-\Delta {\epsilon }_{ij}^P\\ & =\Delta {\epsilon }_{ij}-\sum _{\beta }{\mu }_{ij}^{(\beta )}\Delta {\gamma }^{(\beta )}\\ & =D^{\ast }\Delta t\end{array}$$
由此得出（3.2.3）。
共转的应力增量$\Delta {\sigma }_{ij}=\stackrel{\nabla }{\sigma }\cdot \Delta t$，结合（2.2.2）和（3.2.1c）可得：
$$\begin{array}{rl}\Delta {\sigma }_{ij}& =[{\stackrel{\nabla }{\sigma }}_{ij}^{\ast }+{\sigma }_{ik}\cdot {\omega }_{kj}^{(\alpha )}{\dot{\gamma }}^{(\alpha )}-{\omega }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}{\dot{\gamma }}^{(\alpha )}]\Delta t\\ & =L_{ijkl}:(\Delta {\epsilon }_{ij}-\Delta {\epsilon }_{ij}^P)-{\sigma }_{ij}\Delta {\epsilon }_{kk}+\sum _{\alpha }[{\sigma }_{ik}\cdot {\omega }_{kj}^{(\alpha )}-{\omega }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}]\Delta {\gamma }^{(\alpha )}\\ & =L_{ijkl}:\Delta {\epsilon }_{ij}-{\sigma }_{ij}\Delta {\epsilon }_{kk}-\sum _{\alpha }[L_{ijkl}:{\mu }_{kl}+{\omega }_{jk}^{(\alpha )}\cdot {\sigma }_{ki}+{\omega }_{ik}^{(\alpha )}\cdot {\sigma }_{kj}]\Delta {\gamma }^{(\alpha )}\end{array}$$

---

 利用线性差值函数，通过给定的应变增量$\Delta {\epsilon }_{ij}$求出特定滑移系上的剪切应变$\Delta {\gamma }^{(\alpha )}$，将增量关系（3.2.2）和（3.2.3）代入（3.1.4）：
$$\begin{array}{rl}& \sum _{\beta }\left\{{\delta }_{\alpha \beta }+\theta \Delta t\frac{\partial {\dot{\gamma }}^{(\alpha )}}{\partial {\tau }^{(\alpha )}}\left[L_{ijkl}{\mu }_{kl}^{(\alpha )}+{\omega }_{ik}^{(\alpha )}{\sigma }_{jk}+{\omega }_{jk}^{(\alpha )}{\sigma }_{ik}\right]{\mu }_{ij}^{(\beta )}-\theta \Delta t\frac{\partial {\dot{\gamma }}^{(\alpha )}}{\partial g^{(\alpha )}}{h}_{\alpha \beta }\mathrm{sign}\left({\dot{\gamma }}^{(\beta }\right)\right\}\Delta {\gamma }^{(\beta )}\\ & ={\dot{\gamma }}^{(\alpha )}\Delta t+\theta \Delta t\frac{\partial {\dot{\gamma }}^{(\alpha )}}{\partial {\tau }^{(\alpha )}}\left[L_{ijkl}{\mu }_{kl}^{(\alpha )}+{\omega }_{ik}^{(\alpha )}{\sigma }_{jk}+{\omega }_{jk}^{(\alpha )}{\sigma }_{ik}\right]\Delta {\epsilon }_{ij}\end{array}\text{\hspace{1em}(3.2.5)}$$
其中${\delta }_{\alpha \beta }$为Kronecker delta。一旦通过应变增量$\Delta {\epsilon }_{ij}$求出特定滑移系上的剪切应变$\Delta {\gamma }^{(\alpha )}$，其他增量通过（3.2.2）-（3.2.4）求出。

---

补充：式（3.2.5）中的 $\frac{\partial {\dot{\gamma }}^{(\alpha )}}{\partial {\tau }^{(\alpha )}}$和$\frac{\partial {\dot{\gamma }}^{(\alpha )}}{\partial g^{(\alpha )}}$是通过2.3部分的率相关的滑移本构求出的。

---

3.3 晶格旋转

 在晶体变形过程中，晶格经受畸变和旋转；然而，第2章中当所有的率方程都是建立在旋转坐标系上（2.1.2ab）晶体旋转没有明显包含在本构方程中（Asaro and Rice,1977 和 Asaro,1983b 也是如此）。在变形后的构型中，晶格变形和旋转通过相互垂直的向量，$s^{\ast (\alpha )}$滑移方向向量和$m^{\ast (\alpha )}$滑移面法向向量表示。对方程（2.1.2 a，b）微分：
$${\dot{s}}^{\ast (\alpha )}=(D^{\ast }+{\Omega }^{\ast })\cdot s^{\ast (\alpha )}\text{\hspace{1em}(3.3.1a)}$$
$${\dot{m}}^{\ast (\alpha )}=-m^{\ast (\alpha )}\cdot (D^{\ast }+{\Omega }^{\ast })\text{\hspace{1em}(3.3.1b)}$$

---

详细推导可见(2.2.4)的补充推导

---

相应的增量形式用应变增量$\Delta {\epsilon }_{ij}$和所有滑移系上的滑移增量$\Delta {\gamma }^{(\alpha )}$表示：$$\Delta s_i^{\ast (\alpha )}=\left\{\Delta {\epsilon }_{ij}+{\Omega }_{ij}\Delta t-\sum _{\beta }\left[{\mu }_{ij}^{(\beta )}+{\omega }_{ij}^{(\beta )}\right]\Delta {\gamma }^{(\beta )}\right\}{s}_j^{\ast (\alpha )}\text{\hspace{1em}(3.3.2a)}$$
$$\Delta m_i^{\ast (\alpha )}=-m_j^{\ast (\alpha )}\left\{\Delta {\epsilon }_{ji}+{\Omega }_{ji}\Delta t-\sum _{\beta }\left[{\mu }_{ji}^{(\beta )}+{\omega }_{ji}^{(\beta )}\right]\Delta {\gamma }^{(\beta )}\right\}\text{\hspace{1em}(3.3.2b)}$$
$\Delta s_i^{\ast (\alpha )}$和$\Delta m_i^{\ast (\alpha )}$每一步都要更新，以得到在式（3.2.1a,b）中的定义的当前构型的“Schmid 因子”${\mu }_{ij}^{(\alpha )}$ 和张量${\omega }_{ij}^{(\alpha )}$。

3.4 非线性增量方程

 在这一节中，滑移系的滑移应变${\gamma }^{(\alpha )}$增量方程（3.1.2）不是通过Taylor展开式（3.1.3）求解的。在3.2和3.3节中，除了方程（3.2.5）所有增量方程在这一节中适用，且在时间增量步末尾计算应力和状态变量增量。滑移系上的滑移应变增量$\Delta {\gamma }^{(\beta )}$的求解方法从线性方程（3.2.5）换成了非线性方程，非线性方程是将滑移率的通用表达式（2.3.1）代入增量方程（3.1.2）：
$$\Delta {\gamma }^{(\alpha )}-(1-\theta )\Delta t{\dot{\gamma }}_t^{(\alpha )}-\theta \Delta t{\dot{a}}^{(\alpha )}{f}^{(\alpha )}\left(\frac{{\tau }_t^{\alpha }+\Delta {\tau }^{\alpha }}{g_t^{\alpha }+\Delta g^{\alpha }}\right)=0\text{\hspace{1em}(3.4.1)}$$
其中，$\Delta {\gamma }^{(\alpha )}$与分切应力增量$\Delta {\tau }^{(\alpha )}$的关系式（3.2.3）以及与当前强度$\Delta g^{(\alpha )}$的关系式为非线性的。利用Newton-Rhapson迭代法求解以上非线性方程，线性解（3.2.5）为初始试探值。所有其他增量的求解采取相同的积分过程。

4. ABAQUS子程序

4.1 UMAT

  为了在abaqus实现第3章中向前梯度积分的单晶塑性本构，编写umat子程序。子程序中包含小变形理论和有限变形和有限旋转理论。附录A讨论UMAT子程序的input文件，单晶圆棒拉伸的input文件实例在附录C中。

  单晶UMAT子程序的解相关状态变量包含所有滑移系上的当前强度$g^{(\alpha )}$，剪切应变 ${\gamma }^{(\alpha )}$， 分切应力${\tau }^{(\alpha )}$，滑移面法向$m^{(\ast \alpha )}$，滑移方向$s^{(\ast \alpha )}$以及累计滑移量$\gamma$。解相关状态变量的输出形式详见附录B。应力，应变和状态变量通过ABAQUS求解。当调用子程序时，主程序提供了增量步起始时的状态(应力，解相关的状态变量)和（预估的）应变增量以及时间增量。UMAT子程序执行2个函数：在时间步末尾更新应力以及解相关状态变量，为本构模型提供材料的Jacobian矩阵 $\partial \Delta \sigma /\partial \Delta \epsilon$。Jacobian矩阵依赖于第三章向前梯度时间积分，因为单晶模型是率相关的，在子程序进行数值积分。

  子程序提供两种应力和解相关状态变量的更新方案，一种是3.1-3.3节线性方案的在增量步起始通过线性方程进行更新，或者是3.4节非线性方案通过Newton-Rhapson迭代在增量末端进行更新。当增量方程是稳定的非线性方案允许较长的时间增量步。在Newton-Rhapson迭代方案中，对Jacobian矩阵 $\partial \Delta \sigma /\partial \Delta \epsilon$ 进行简化，忽略滑移面法向和滑移方向增量对应变增量的导数$\frac{\partial \Delta m^{\ast }}{\partial \Delta \epsilon }$ 和$\frac{\partial \Delta s^{\ast }}{\partial \Delta \epsilon }$。当不考虑晶格旋转简化不产生误差。如果考虑晶格旋转，误差是弹性应变增量的量级，与1比为 $O(D^{\ast }\Delta t)$。

  在当前版本abaqus主程序和umat子程序的接口中，没有提供方程（3.3.2a,b）中的增量${\Omega }_{ij}\Delta t$，可以通过旋转增量矩阵$\Delta R$求出：
$$\mathbf{\Delta }\mathbf{R}={\left(\mathbf{I}-\frac{1}{2}\mathbf{\Omega }\mathbf{\Delta }\mathbf{t}\right)}^{-1}\cdot \left(\mathbf{I}+\frac{1}{2}\mathbf{\Omega }\mathbf{\Delta }\mathbf{t}\right)\text{\hspace{1em}(4.1.1)}$$
(abaqus 理论手册，1989)

---

已知 $\Omega =\dot{R}{R}^T$

$$\Delta R=\frac{1}{2}[\dot{R}(t+\Delta t)+\dot{R}(t)]\Delta t$$
$$R(t+\Delta t)-R(t)=\frac{1}{2}[$$