31线性变换及其矩阵

一、线性变换的概念

一个线性变换 $T$ 将空间 $V$ 中的所有向量变换成 $T(\mathbf{v})$，如果这种变换任意想来给你 $\mathbf{w}$ $\mathbf{v}$ 满足以下条件，那么它是一个线性变换。

• $T(\mathbf{v}+w)=T(\mathbf{v})+T(\mathbf{w})$
• $T(c\mathbf{v})=cT(\mathbf{v})$

当然我们也可以将条件写成一个：
$$T(c\mathbf{v}+d\mathbf{w})=cT(\mathbf{v})+dT(\mathbf{w})\text{\hspace{1em}(1)}$$
变换是映射，它将一个事物对应成另一个事物，在所有映射中，满足线性条件的映射叫做线性变换。来几个对线性变换的感性认识：

平移变换(Shift transformation) 不是一个线性变换 $T$：输入向量叠加上一个固定向量${\mathbf{u}}_0$ 。根据概念，它不是一个线性变换，因为$(1)$ 的左边：
$$T(c\mathbf{v}+d\mathbf{w})=c\mathbf{v}+d\mathbf{w}+{\mathbf{u}}_0$$
右边：
$$T(c\mathbf{v})+T(d\mathbf{w})=c\mathbf{w}+d\mathbf{v}+2{\mathbf{u}}_0$$
也就是：
$$T(c\mathbf{v}+d\mathbf{w})\ne T(c\mathbf{v})+T(d\mathbf{w})$$
当然如果${\mathbf{u}}_0=0$，也是一个线性变换，这种变换叫做单位变换（Identity transformation）。

矩阵乘法是一个线性变换 $T$ ：输入向量左乘一个固定矩阵 $A$。根据概念，左边$T(c\mathbf{v}+d\mathbf{w})=cA\mathbf{v}+dA\mathbf{w}=T(c\mathbf{v}+d\mathbf{w})$

仿射变换(Affine transformation)不是一个线性变换 T：$A\mathbf{v}+{\mathbf{u}}_0$。

二、更多例子

2.1 选择一个固定向量 $\mathbf{a}=(1,3,4)$，让变换为 $T(\mathbf{v})$ ：$\mathbf{a}\cdot \mathbf{v}$

它是一个线性变换。假设输入向量是 $\mathbf{v}=(v_1,v_2,v_3)$。可以看出输入向量是一个属于 $R^3$ 空间，但是其结果是一个数，也就是 $R^1$ 空间，它相当于左乘了一个矩阵$A=[1,3,4]$，前面讨论过，左乘一个矩阵是一个线性变换。

2.2 变换为取模 $T(\mathbf{v})=||v||$

它不是一个线性变换。因为既不满足 $||v+w||=||v||+||w||$ ，也不满足 $||-v||=-||v||$ 。

2.3 变换为$T(v)$ 每个向量都旋转 $30$ 度

旋转可以用一个矩阵来表示，属于左乘一个矩阵的情况，故为线性变换。

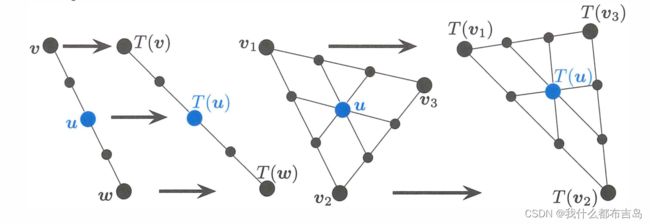
2.4 线到线，三角到三角的线性变换在图形上的特点

如果我们把这些向量用图形表示出来，比如在直线上：

上图，向量$\mathbf{u}=0.5(\mathbf{v}+\mathbf{w})$，如果进行了线性变换，那么变换前后各点的距离相等关系是不变的。同理对于$R^2$空间的三个向量， 重心公式为：$\mathbf{u}=1/3({\mathbf{v}}_1+{\mathbf{v}}_2+{\mathbf{v}}_3)$ 经过线性变换后距离相等公式不变，且重心公式$1/3(T({\mathbf{v}}_1)+T({\mathbf{v}}_2)+T({\mathbf{v}}_3))$。

2.5 T：$R^3\to R^2$

$$T(v)=Av$$
输入向量$v\in R^3$，也就是说矩阵 $A$ 必须为一个 $2\times 3$ 的矩阵，输出向量是一个在 $R^2$的矩阵。事实上，所有线性变换都可以用一个矩阵来表示。

三、线性变换的矩阵表达

结论：所有线性变换都可以通过一个矩阵来表示。

给定输入向量 $v$ 及其所属空间：

向量名称	空间名称	空间维数
$v$	$V$	$R^n$
$T(v)$ or $w$	$W$	$R^m$

我们的目标：找到线性变换对应的找到一个矩阵 $A$ ，使得输入向量都能很轻松的通过左乘 $A$ 获得到输出向量。也就是是
$$w=Av$$
OK！我们来看看这个对应的矩阵与什么有关：

• 输入输出向量维数使得矩阵的尺寸必须是 $m\times n$，也就是输出维数乘以输入维数；
• 表示输入向量的基和输出向量的基

为什么选择不同的基会影响我们的线性变换矩阵？答：选择不同的基对应的坐标值就会不同，如果坐标值改变了，那么相应的矩阵也会做相应的更改。输入向量 $v$：
$$v=c_1{v}_1+c_2{v}_2+\cdots +c_n{v}_n$$
根据线性变换性质有：
$$T(v)=c_{1}T(v_1)+c_{2}T(v_2)+\cdots +c_{n}T(v_n)$$
经过线性变换后的线性“新”基，表示了新空间 $W$的向量 $w=T(v)$。对于这个向量 $w$ 除了可以用线性新基表示，还可以是另外一组基如：$w_1,w_2,\cdots ,w_m$。也就是：
$$c_{1}T(v_1)+c_{2}T(v_2)+\cdots +c_{n}T(v_n)=d_1{w}_1+d_2{w}_2+\cdots +d_n{w}_m$$
写成矩阵形式：
$$\begin{array}{rl}\left[\begin{array}{cccc}T(v_1)& T(v_2)& \cdots & T(v_n)\end{array}\right]C& =\left[\begin{array}{ccc}{w}_1& w_2\cdots & w_m\end{array}\right]D\\ T_{V}C& =WD\end{array}$$
我们要求的矩阵是：$A=T_V{W}^{-1}$。

例子：输入基为：$1,x,x^2,x^3$ ，其线性变换 $T$ 是微分，对应输出基为 $1,x,x^2$。

设完成这个转换的矩阵为 $A$，我们按列写出这个矩阵。步骤是，取输入基，进行进行线性变换，$T(1)=0$，对应的输出基没有可以表示这个的基，故为 [ 0 0 0 ] \begin{bmatrix}0\\0\\0\end{bmatrix} ​000​ ​，输入基第二个 $T(x)=1$，输出基线性表示为 [ 1 0 0 ] \begin{bmatrix}1\\0\\0\end{bmatrix} ​100​ ​，同理有： [ 0 2 0 ] \begin{bmatrix}0\\2\\0\end{bmatrix} ​020​ ​ [ 0 0 3 ] \begin{bmatrix}0\\0\\3\end{bmatrix} ​003​ ​，所以所求的矩阵为：
A = [ 0 1 0 0 0 0 2 0 0 0 0 3 ] A=\begin{bmatrix}0&1&0&0\\0&0&2&0\\0&0&0&3\end{bmatrix} A= ​000​100​020​003​ ​
如果已知输入基的坐标为 C = [ c 1 c 2 c 3 c 4 ] C=\begin{bmatrix}c_1\\c_2\\c_3\\c_4\end{bmatrix} C= ​c1​c2​c3​c4​​ ​，那么输出的系数可以轻松得到：
A C = [ c 2 2 c 3 3 c 3 ] AC=\begin{bmatrix}c_2\\2c_3\\3c_3\end{bmatrix} AC= ​c2​2c3​3c3​​ ​