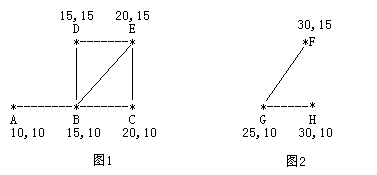一本通 3.4.2 图的最短路径
《Floyd算法》
算法思想:定义状态D(Ki,j)为经过前k个点i到j的最短路径,动态转移方程:D(k,i,j)=min(D(k-1,i,i),D(k-1,i,k)+D(k-1,k,j))
k层的前面的计算不会影响后面的计算,可以使用滚动数组进行存储,节省存储空间,D(i,j)=min(D(i,j),D(i,k)+D(k,j))
初始状态:D(i,i)=0,D(i,j)=e(i,j)
算法过程:https://blog.csdn.net/xuqw11111/article/details/128503150
算法分析:
(1) Floyd算法可以解决带有负权边的图,但不能判断是否带有“负权回路”的图(带有负权回路的图是没有最短路径的)
(2) Floyd算法的时间复杂度为O(n^3),主要解决多源最短路径问题(任意两点之间的最短路径)。
路径追踪:使用二维数组进行过程记录,rec(i,j)=k表示从i点到j点经过k点路径最短,递归输出rec(i,k) 和输出rec(k,j)
《Dijstra算法》
算法思想:从起点开始,每次寻找最近的点通过相连边对其他点进行松弛操作
算法过程:https://blog.csdn.net/xuqw11111/article/details/128503160
常规过程:
1、找路径dis中最短的点i 时间复杂度为n
2、i的邻边松弛dis中的数值 总的时间复杂度为m
3、循环n次 总的时间复杂度为O(m+n*n) 可以记为O(n*n) 数据复杂度N≤10^3
优化过程:
1、使用优先队列记录路径dis的距离和点编号,每次弹出最短的估计距离点i,弹出队列表示该距离点从估计值变为最短值,标记vis[i]
2、邻接表记录边信息,根据弹出的点判断是否已经标记,无标记使用邻边进行松弛操作。
3、重复执行上述过程,直到队列为空 程序时间复杂度为 MlogM 数据复杂度N≤10^6 M≤10^6
算法实现
算法分析
(1) Dijkstra算法无法解决带有负权边的图(在该算法每步松弛过程后认为找到的最短估计值已经是最短距离,如果后续还有点可以通过负边到达原来的点,使原来的点距离变得更短,那么后面做的工作就是不正确的了)。
(2) Dijkstra算法的时间复杂度为O(n^2),主要解决单源最短距离问题(由源点都任意一点之间的最短距离)。
(3) Dijkstra算法是使用明确边对最短路进行松弛操作,当边的数量远大于点的数量时,该算法可以实现较好的效果。
追踪过程:使用一维数组记录每个点的最短路径是由前面哪个点得到
《Ballman算法》
算法思想:通过不断的加边,使所有点的距离最小
算法过程:https://blog.csdn.net/xuqw11111/article/details/128503168
1、初始化dis的距离为inf,并将dis[start]=0
2、将所有边加入,对所有顶点进行松弛操作(第一次循环只有和start相连的点松弛成功)
3、上面的循环执行n次
4、当所有边的加入都不能松弛成功时,退出外层n的循环 ,判断循环次数如果为n说明存在负环
时间复杂度为O(N*M) 数据范围N<10^3 M<10^3
算法实现
算法分析
(1) Bellman算法可以解决带有负权边的图,(该算法是使用边对所有顶点进行松弛操作,而且操作的次数为n-1,可以优化起点到最远终点的最短距离)。
(2) Bellman算法的时间复杂度为O(mn),其中m为边的数量,n为点的数量, 主要解决单源最短距离问题(由源点都任意一点之间的最短距离)。
(3) Bellman算法可以判定是否存在环路。如果对于不存在负权回路的图进行n-1次松弛后就可以得到最短距离,后面再进行松弛,理论上不会影响所有最短距离,如果影响最短路说明存在负权回路。
路径追踪:使用rec一维数组记录每个点松弛操作的前驱节点,直到数组内容为0停止,使用栈或者递归进行输出
《SPFA算法》
算法思想:对Bellman算法的优化,每次仅对最短路估计值发生变化了的顶点所有出边进行松弛操作
算法过程:https://blog.csdn.net/xuqw11111/article/details/128503181
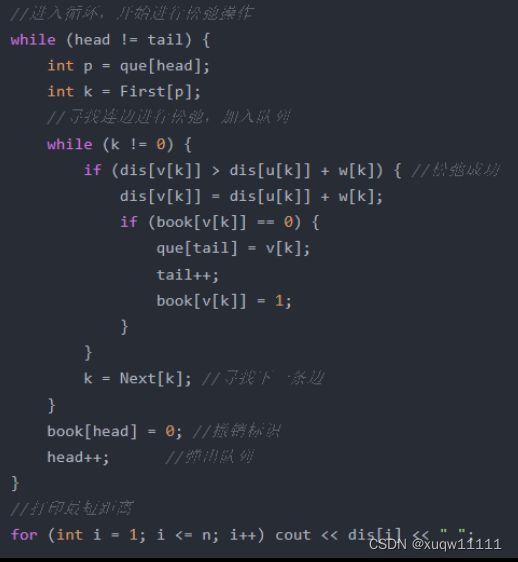
1、将起点加入队列并将dis[start]=0,标记vis[start]=1 进入循环,循环条件为队列不为空
2、弹出队列队首,清除标记vis[head]=0,使用队首的所有出边对所有相连顶点进行松弛操作,如果松弛成功将相邻顶点加入队列 标记vis=1
特别的:保证队列中同时不能出项重复的点,队首出队后将重复标识置为0
时间复杂度 O(k*M) 其中k
算法实现
路径追踪:使用一维rec数组进行每个点松弛的前驱节点,使用栈或者递归进行数据输出
1342:【例4-1】最短路径问题
【题目描述】
平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。
若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。
【题目分析】
数据范围为100以内,可以使用Floyed算法,本题将坐标点进行编号,坐标点间距使用开根号求得,给坐标系中点的最短路径问题提供了一种思路
使用二维数组或者两个一维数组进行坐标点的存储,读入坐标点的连接关系,使用实数类型的二维数组进行点和距离的存储,调用Floyed算法求解最短路径,输出任意两点之间的最短距离
【代码实现】
#include
using namespace std;
//points
int px[101], py[101];
//edges
double dis[101][101];
int main() {
//input data
int n, m;
//input points
cin >> n;
for (int i = 1; i <= n; i++) {
int x, y;
cin >> x >> y;
px[i] = x, py[i] = y;
}
cin >> m;
//init edges's info
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
if (i == j) dis[i][j] = 0;
else dis[i][j] = dis[j][i] = 0x7fffffff;
}
//input edges's info
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
double len = sqrt((px[x] - px[y]) * (px[x] - px[y]) + (py[x] - py[y]) * (py[x] - py[y]));
dis[x][y] = dis[y][x] = len ;
}
// clock_t s = clock();
//use floyed get anser
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (dis[i][j] > dis[i][k] + dis[k][j])
dis[i][j] = dis[i][k] + dis[k][j];
}
int p1, p2;
cin >> p1 >> p2;
printf("%.2f", dis[p1][p2]);
//output time
// cout < 1343:【例4-2】牛的旅行
【题目描述】
农民John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言,你能看到至少有两个牧区不连通。现在,John想在农场里添加一条路径 ( 注意,恰好一条 )。对这条路径有这样的限制:一个牧场的直径就是牧场中最远的两个牧区的距离 ( 本题中所提到的所有距离指的都是最短的距离 )。考虑如下的两个牧场,图1是有5个牧区的牧场,牧区用“*”表示,路径用直线表示。每一个牧区都有自己的坐标:
图1所示的牧场的直径大约是12.07106, 最远的两个牧区是A和E,它们之间的最短路径是A-B-E。
这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。注意,如果两条路径中途相交,我们不认为它们是连通的。只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,这个更大的新牧场有最小的直径。
【题目分析】
使用Floyed算法计算任意两个牧区之间的最短路径,使用数组dis[i]记录i牧区到其他相连牧区的最长距离。
记录两个牧场中最大的一个直径 r1=max(dis[i]),枚举任意两个不相连的牧区i j,寻找r2=min(dis[i]+dis[j]+(i,j)的距离),更大的新牧场有最小的直径 r=max(r1,r2)。
【代码实现】
#include
#define N 200
#define max_double 1e9
using namespace std;
double dis[N][N];
double max_dis[N];
int n;
int px[N], py[N];
void readdata() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> px[i] >> py[i];
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
char w;
cin >> w;
if (i == j) dis[i][j] = 0;
else if (w == '0') dis[i][j] = dis[j][i] = max_double;
else {
double temp = sqrt((px[i] - px[j]) * (px[i] - px[j]) + (py[i] - py[j]) * (py[i] - py[j]));
dis[i][j] = dis[j][i] = temp;
};
}
}
void floyed() {
//floyed
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (dis[i][j] > dis[i][k] + dis[k][j])
dis[i][j] = dis[i][k] + dis[k][j];
}
}
void find() {
double r1 = 0;
// find every point's long distance
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (max_dis[i] < dis[i][j] && dis[i][j] < max_double - 1) {
max_dis[i] = dis[i][j];
if (r1 < max_dis[i]) r1 = max_dis[i];
}
double r2 = max_double;
// find no connect long distance
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (i!=j && dis[i][j] > max_double - 1) {
double temp = sqrt((px[i] - px[j]) * (px[i] - px[j]) + (py[i] - py[j]) * (py[i] - py[j]));
r2 = min(r2, max_dis[i] + max_dis[j] + temp);
// cout< 1344:【例4-4】最小花费
【题目描述】
在n个人中,某些人的银行账号之间可以互相转账。这些人之间转账的手续费各不相同。给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问A最少需要多少钱使得转账后B收到100元。
【题目分析】
使用dijstra算法求解A到B的最短路径Z,A的需要转入的最少金额为100/(1-Z/100.0)
【代码实现】
#include
using namespace std;
int m,n;
double e[2005][2005];
int main() {
//input data
// clock_t s = clock();
cin>>n>>m;
//init data
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j) e[i][j]=1;
else e[i][j]=-1;
}
}
//input data
for(int i=1;i<=m;i++)
{
int x,y;
double w;
cin>>x>>y>>w;
e[x][y]=e[y][x]=(100-w)/100;
}
//floyed algo
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(i!=j && e[i][j]>x>>y;
printf("%.8f",100/e[x][y]);
//output time
// cout << endl << clock() - s << endl;
return 0;
} #include
using namespace std;
int m, n;
double e[2005][2005];
double dis[2005];
int book[2005];
int main() {
//input data
// clock_t s = clock();
cin >> n >> m;
//init data
for (int i = 1; i <= n; i++) {
dis[i] = -1;
for (int j = 1; j <= n; j++) {
if (i == j) e[i][j] = 1;
else e[i][j] = -1;
}
}
//input data
for (int i = 1; i <= m; i++) {
int x, y;
double w;
cin >> x >> y >> w;
e[x][y] = e[y][x] = (100 - w) / 100;
}
int x, y;
cin >> x >> y;
dis[x] = 1; //init dis values
//dijkstra algo
for (int i = 1; i <= n; i++) { //find n-1 points,last point is queding
//find large point
double maxvalue = -1;
int index = 0;
for (int j = 1; j <= n; j++) {
if (maxvalue < dis[j] && book[j] == 0) {
maxvalue = dis[j];
index = j;
}
}
book[index] = 1;
if (index == y) break;
//connect edges to make dis value
for (int j = 1; j <= n; j++) {
if (e[index][j] > 0 && book[j] == 0) { //connect edges
if (dis[j] < dis[index]*e[index][j])
dis[j] = dis[index] * e[index][j];
}
}
}
// for (int i = 1; i <= n; i++) {
// cout << dis[i] << " ";
// }
printf("%.8f", 100 / dis[y]);
//output time
// cout << endl << clock() - s << endl;
return 0;
} 1345:【例4-6】香甜的黄油
【题目描述】
农夫John发现做出全威斯康辛州最甜的黄油的方法:糖。把糖放在一片牧场上,他知道N(1≤N≤500)只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。当然,他将付出额外的费用在奶牛上。
农夫John很狡猾。像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
【题目分析】
分析问题:A B两个牧场之间的距离为A到B:a*dis(A,B) a为A牧场的牛数,A到B:b*dis(A,B) b为B牧场的牛数。
使用上面的规则更新牧场间权值,使用Floyed计算任意两个牧场之间的最短距离,枚举每个牧场寻找其他牧场到该牧场的最小距离和。
【代码实现】
#include
using namespace std;
int n, m, p;
int pn[505], e[805][805];
int dis[805];
int book[805];
int maxint = 0x3f3f3f3f;
struct Edge {
int next;
int to;
int dis;
} edge[3000];
int head[805], u, v, w, num_edge = 0;
void add_edge(int from, int to, int dis) {
edge[++num_edge].next = head[from];
head[from] = num_edge;
edge[num_edge].to = to;
edge[num_edge].dis = dis;
}
int main() {
//input data
//clock_t s = clock();
cin >> p >> n >> m;
for (int i = 1; i <= p; i++)
cin >> pn[i];
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add_edge(x, y, z);
add_edge(y, x, z);
}
long long ans = maxint;
long long pans = 0;
for (int k = 1; k <= n; k++) {
//init dis and book
memset(dis, 0x3f, sizeof(dis));
memset(book, 0, sizeof(book));
//init dijkstra
dis[k] = 0;
for (int i = 1; i <= n - 1; i++) {
int index = 0;
int minval = maxint;
for (int j = 1; j <= n; j++)
if (minval > dis[j] && book[j] == 0) {
index = j;
minval = dis[j];
}
book[index] = 1;
int j = head[index];
while (j != 0) {
int v = edge[j].to;
if (dis[v] > dis[index] + edge[j].dis)
dis[v] = dis[index] + edge[j].dis;
j = edge[j].next;
}
}
pans = 0;
for (int i = 1; i <= p; i++) {
pans += dis[pn[i]];
}
if (ans > pans) ans = pans;
}
cout << ans << endl;
//output time
//cout < #include
using namespace std;
int maxint = 0x3f3f3f3f;
int n, m, p;
int pn[505];
int dis[805];
struct Edge {
int from;
int to;
int dis;
} edge[3000];
int main() {
//input data
//clock_t s = clock();
cin >> p >> n >> m;
for (int i = 1; i <= p; i++)
cin >> pn[i];
for (int i = 1; i <= m; i++) {
int m = 2 * i;
cin >> edge[m - 1].from >> edge[m - 1].to >> edge[m - 1].dis;
edge[m].from = edge[m - 1].to;
edge[m].to = edge[m - 1].from;
edge[m].dis = edge[m - 1].dis;
}
int ans = maxint;
int pans = 0;
for (int k = 1; k <= n; k++) {
bellman-ford
memset(dis, 0x3f, sizeof(dis));
dis[k] = 0;
for (int i = 1; i <= n - 1; i++) {
bool flag = 0;
for (int j = 1; j <= m; j++) {
struct Edge e = edge[2 * j - 1];
if (dis[e.to] > dis[e.from] + e.dis) {
dis[e.to] = dis[e.from] + e.dis;
flag = 1;
}
e = edge[2 * j];
if (dis[e.to] > dis[e.from] + e.dis) {
dis[e.to] = dis[e.from] + e.dis;
flag = 1;
}
}
if (flag == 0) break;
}
pans = 0;
for (int i = 1; i <= p; i++) {
pans += dis[pn[i]];
}
if (ans > pans) ans = pans;
}
cout << ans << endl;
//output time
//cout < 1376:信使(msner)
【题目描述】
战争时期,前线有n个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。指挥部设在第一个哨所。当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。直至所有n个哨所全部接到命令后,送信才算成功。因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他k个哨所有通信联系的话,这个哨所内至少会配备k个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
【题目分析】
使用Dijstra算法计算从1号哨所到其他哨所的最短传递时间,寻找其中最长的传递时间为结果,如果其中存在inf时间,则输出-1
【代码实现】
#include
using namespace std;
const int maxn = 105;
const int maxm = 10005;
int e[maxn][maxn];
int n, m;
int dis[maxn];
int maxint = 1e7;
int book[maxn];
int main() {
//input data
//clock_t s = clock();
cin >> n >> m;
for (int i = 1; i <= n; i++) {
dis[i] = maxint;
for (int j = 1; j <= n; j++) {
if (i == j) e[i][j] = 0;
else e[i][j] = maxint ;
}
}
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
e[x][y] = e[y][x] = z;
}
dis[1] = 0;
for (int i = 1; i <= n - 1; i++) {
//find min dis
int index = 0, minval = maxint;
for (int j = 1; j <= n; j++) {
if (minval > dis[j] && book[j] == 0) {
index = j;
minval = dis[j];
}
}
book[index] = 1;
for (int j = 1; j <= n; j++) {
if (e[index][j] < maxint)
dis[j] = min(dis[j], dis[index] + e[index][j]);
}
}
int maxval = 0;
for (int i = 1; i <= n; i++) {
if (maxval < dis[i]) maxval = dis[i];
}
cout< 1377:最优乘车(travel)
【题目描述】
H城是一个旅游胜地,每年都有成千上万的人前来观光。为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,最终到达终点巴士站。
一名旅客最近到H城旅游,他很想去S公园游玩,但如果从他所在的饭店没有一路巴士可以直接到达S公园,则他可能要先乘某一路巴士坐几站,再下来换乘同一站台的另一路巴士, 这样换乘几次后到达S公园。
现在用整数1,2,…N 给H城的所有的巴士站编号,约定这名旅客所在饭店的巴士站编号为1,S公园巴士站的编号为N。
写一个程序,帮助这名旅客寻找一个最优乘车方案,使他在从饭店乘车到S公园的过程中换车的次数最少。
【题目分析】
问题求解:从饭店乘车到S公园的过程中换车的次数最少
问题转化:将同一辆公交可达的站点之间的边权赋值为1,其他值为inf,使用dijstra算法求解最短路径即可
特别的:同一辆公交可达的站点之间的边权都为1,不同公交之间使用1+1进行最短路径求解
【代码实现】
#include
using namespace std;
const int maxn = 505;
const int maxint = 0x3f3f3f3f;
int n, m;
int e[maxn][maxn];
int dis[maxn];
int book[maxn];
int main() {
//input data
//clock_t s = clock();
string s;
cin >> m >> n;
getline(cin, s);
// init edges info
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) e[i][j] = 0;
else e[i][j] = e[j][i] = maxint;
}
}
// cout<= '0' && s[j] <= '9') {
num[_count] = num[_count] * 10 + s[j] - '0';
} else {
// if (_count != 1) //is processing deal
// for (int k = 1; k < _count; k++)
// e[num[k]][num[_count]] = 1;
_count++;
}
}
for (int j = 1; j <= _count; j++) //is last deal
for (int k = j + 1; k <= _count; k++)
e[num[j]][num[k]] = 1;
}
//dijkstra
memset(dis, 0x3f, sizeof(dis));
dis[1] = 0;
for (int i = 1; i <= n - 1; i++) {
//find min point
int index = 0, minval = maxint;
for (int j = 1; j <= n; j++)
if (book[j] == 0 && dis[j] < minval) {
minval = dis[j];
index = j;
}
book[index] = 1;
//updata dis data
for (int j = 1; j <= n; j++) {
if (e[index][j] < maxint)
dis[j] = min(dis[j], dis[index] + e[index][j]);
}
}
if (dis[n] > maxint - 1)
cout << "NO" << endl;
else
cout << dis[n] - 1 << endl;
//output time
//cout < 1378:最短路径(shopth)
【题目描述】
给出一个有向图G=(V, E),和一个源点v0∈V,请写一个程序输出v0和图G中其它顶点的最短路径。只要所有的有向环权值和都是正的,我们就允许图的边有负值。顶点的标号从1到n(n为图G的顶点数)。
【题目分析】
数据的读入:读入行,设置数值变量num,与标记变量flag,依次读入字符为c,如果c为'-',flag=1,如果c为数字,num=num*10+c-'0',如果c为空格,flag==1 且 num==0 该连接距离为inf,flag==1 且num!=0 该连接距离为-num,其他情况连接距离为num
因为有负权边,数据范围不大,使用bellman算法
【代码实现】
#include
using namespace std;
const int maxn = 1005;
const int maxint = 0x3f3f3f3f;
int n, start;
int e[maxn][maxn];
int dis[maxn], book[maxn];
int main() {
//input data
//clock_t s = clock();
string s;
cin >> n >> start;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
int a;
if (scanf("%d", &a) == 1) e[i][j] = a;
else e[i][j] = maxint;
}
}
//floyed
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (e[i][j] > e[i][k] + e[k][j]) e[i][j] = e[i][k] + e[k][j];
}
}
}
for (int i = 1; i <= n; i++) {
if (i == start) continue;
printf("(%d -> %d) = %d\n", start, i, e[start][i]);
}
//output time
//cout < 1379:热浪(heatwv)
【题目描述】
德克萨斯纯朴的民眾们这个夏天正在遭受巨大的热浪!!!他们的德克萨斯长角牛吃起来不错,可是他们并不是很擅长生產富含奶油的乳製品。Farmer John此时以先天下之忧而忧,后天下之乐而乐的精神,身先士卒地承担起向德克萨斯运送大量的营养冰凉的牛奶的重任,以减轻德克萨斯人忍受酷暑的痛苦。
FJ已经研究过可以把牛奶从威斯康星运送到德克萨斯州的路线。这些路线包括起始点和终点先一共经过T (1 <= T <= 2,500)个城镇,方便地标号為1到T。除了起点和终点外的每个城镇由两条双向道路连向至少两个其它的城镇。每条道路有一个通过费用(包括油费,过路费等等)。
给定一个地图,包含C (1 <= C <= 6,200)条直接连接2个城镇的道路。每条道路由道路的起点Rs,终点Re (1 <= Rs <= T; 1 <= Re <= T),和花费(1 <= Ci <= 1,000)组成。求从起始的城镇Ts (1 <= Ts <= T)到终点的城镇Te(1 <= Te <= T)最小的总费用。
【题目分析】
模板题,使用dijstra算法或者bellman算法或者SPFA算法
【代码实现】
#include
using namespace std;
const int maxn = 2501;
int inf = 0x3f3f3f3f;
int n, m, x, y;
int e[maxn][maxn];
int dis[maxn],book[maxn];
int main() {
//input data
//clock_t s = clock();
cin >> n >> m >> x >> y;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) e[i][j] = 0;
else e[i][j] = e[j][i] = inf;
}
}
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
e[x][y] = e[y][x] = z;
}
//dijkstra
memset(dis, 0x3f, sizeof(dis));
dis[x] = 0;
for (int i = 1; i <= n - 1; i++) {
//find min point
int index = 0, minval = inf;
for (int j = 1; j <= n; j++)
if (book[j] == 0 && dis[j] < minval) {
minval = dis[j];
index = j;
}
if(index==y) break;
book[index] = 1;
//updata dis data
for (int j = 1; j <= n; j++) {
if (e[index][j] < inf)
dis[j] = min(dis[j], dis[index] + e[index][j]);
}
}
cout< 1380:分糖果(candy)
【题目描述】
童年的我们,将和朋友分享美好的事物作为自己的快乐。这天,C小朋友得到了Plenty of candies,将要把这些糖果分给要好的朋友们。已知糖果从一个人传给另一个人需要1 秒的时间,同一个小朋友不会重复接受糖果。由于糖果足够多,如果某时刻某小朋友接受了糖果,他会将糖果分成若干份,分给那些在他身旁且还没有得到糖果的小朋友们,而且自己会吃一些糖果。由于嘴馋,小朋友们等不及将糖果发完,会在得到糖果后边吃边发。每个小朋友从接受糖果到吃完糖果需要m秒的时间。那么,如果第一秒C小朋友开始发糖,第多少秒所有小朋友都吃完了糖呢?
【题目分析】
m表示小朋友吃糖的时间,计算起点到各个点的最短距离,寻找其中的最大值+m即为答案
【代码实现】
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 100010;
const int maxm = maxn * 20;
int n, m, s, t;
struct Edge {
int next;
int to;
int dis;
} edge[maxm];
int head[maxn], _count;
void add_edge(int from, int to, int dis) {
edge[++_count].next = head[from];
head[from] = _count;
edge[_count].to = to;
edge[_count].dis = dis;
}
int dis[maxn], mark[maxn];
void spfa(int start) {
memset(dis, 0x3f, sizeof(dis));
memset(mark, 0, sizeof(mark));
queueque;
que.push(start);
mark[start] = 1;
dis[start] = 0;
//不存在负权回路
while (!que.empty()) {
int u = que.front();
que.pop();
mark[u] = 0;
int k = head[u];
while (k != 0) {
int v = edge[k].to;
int u_v = edge[k].dis;
if (dis[v] > dis[u] + u_v) {
dis[v] = dis[u] + u_v; //update dis
if (mark[v] == 0) {
que.push(v);
mark[v] = 1;
}
}
k=edge[k].next;
}
}
}
int main() {
//input data
//clock_t s = clock();
cin >> n >> m >> s;
cin >> t;
for (int i = 1; i <= m; i++) {
int x,y;
cin>>x>>y;
add_edge(x, y, 1);
add_edge(y, x, 1);
}
spfa(1);
int maxtime = 0;
for (int i = 1; i <= n; i++) {
maxtime = max(maxtime, dis[i]);
}
cout << maxtime + t + 1 << endl;
//output time
//cout < #include
using namespace std;
const int inf=0x3f3f3f3f;
const int N=100100;
int dis[N*10];
struct node
{
int from;
int to;
int next;
int dis;
}s[N*20];
int head[N*10]={0};
int vis[N]={0};
int cnt=0;
void add_edge(int from,int to,int dis)
{
s[++cnt].next=head[from];
s[cnt].to=to;
s[cnt].dis=dis;
head[from]=cnt;
}
int n,p,c;
int m;
void spfa(int ss)
{
memset(dis,inf,sizeof(dis));
vis[ss]=1;
dis[ss]=0;
queueQ;
Q.push(ss);
while(!Q.empty()){
int u=Q.front();
Q.pop();
vis[u]=0;
for(int i=head[u];i!=0;i=s[i].next){
int to=s[i].to;
int di=s[i].dis;
if(dis[to]>dis[u]+di){
dis[to]=dis[u]+di;
if(!vis[to]){
vis[to]=1;
Q.push(to);
}
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>p>>c>>m;
memset(head,0,sizeof(head));
for(int i=0;i>x>>y;
add_edge(x,y,1);
add_edge(y,x,1);
}
spfa(c);
int maxn=-1;
for(int i=1;i<=n;i++){
if(maxn 1381:城市路(Dijkstra)
【题目描述】
罗老师被邀请参加一个舞会,是在城市n,而罗老师当前所处的城市为1,附近还有很多城市2~n-1,有些城市之间没有直接相连的路,有些城市之间有直接相连的路,这些路都是双向的,当然也可能有多条。
现在给出直接相邻城市的路长度,罗老师想知道从城市1到城市n,最短多少距离。
【题目分析】
特别的:屏蔽多条道路连接两个点的情况,取矩阵原来值和当前输入值的最小值作为最后距离值
使用dijstra算法/bellman算法/SPFA算法
【代码实现】
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 2005;
const int maxm = 20005;
int n, m;
struct Edge {
int next;
int to;
int dis;
} edge[maxm];
int head[maxn], _count;
void add_edge(int from, int to, int dis) {
edge[++_count].next = head[from];
head[from] = _count;
edge[_count].to = to;
edge[_count].dis = dis;
}
int dis[maxn], mark[maxn];
void Dijkstra(int start) {
//init dis and book
memset(dis, 0x3f, sizeof(dis));
memset(mark, 0, sizeof(mark));
//init dijkstra
dis[start] = 0;
for (int i = 1; i <= n - 1; i++) {
int u = 0;
int minval = inf;
for (int j = 1; j <= n; j++)
if (minval > dis[j] && mark[j] == 0) {
u = j;
minval = dis[j];
}
mark[u] = 1;
int k = head[u];
while (k != 0) {
int v = edge[k].to;
int u_v = edge[k].dis;
dis[v] = min(dis[v], dis[u] + u_v);
k = edge[k].next;
}
}
}
int main() {
//input data
//clock_t s = clock();
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add_edge(x, y, z);
add_edge(y, x, z);
}
Dijkstra(1);
if (dis[n] > inf - 1)
cout << -1 << endl;
else
cout << dis[n] << endl;
//output time
//cout < 1382:最短路(Spfa)
【题目描述】
给定 M条边, N个点的带权无向图。求 1到 N 的最短路。
【题目分析】
特别的:屏蔽多条道路连接两个点的情况,取矩阵原来值和当前输入值的最小值作为最后距离值
SPFA模板题,时间复杂度最坏为NM
优化的Dijstra算法,时间复杂度为mlogm
【代码实现】
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 20005;
const int maxm = 40005;
int n, m;
struct Edge {
int next;
int to;
int dis;
} edge[maxm];
int head[maxn], _count;
void add_edge(int from, int to, int dis) {
edge[++_count].next = head[from];
head[from] = _count;
edge[_count].to = to;
edge[_count].dis = dis;
}
long long dis[maxn];
int mark[maxn];
void spfa(int start) {
memset(dis, 0x3f, sizeof(dis));
memset(mark, 0, sizeof(mark));
queueque;
que.push(start);
mark[start] = 1;
dis[start] = 0;
//不存在负权回路
while (!que.empty()) {
int u = que.front();
que.pop();
mark[u] = 0;
int k = head[u];
while (k != 0) {
int v = edge[k].to;
int u_v = edge[k].dis;
if (dis[v] > dis[u] + u_v) {
dis[v] = dis[u] + u_v; //update dis
if (mark[v] == 0) {
que.push(v);
mark[v] = 1;
}
}
k = edge[k].next;
}
}
}
int main() {
//input data
//clock_t s = clock();
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add_edge(x, y, z);
// add_edge(y, x, z);
}
spfa(1);
cout< 1419:SPFA(II)
【题目描述】
给定一个有向连通图,求从1到n的最短路。
【题目分析】
使用邻接表记录数据,定义long long dis[]的数组,使用SPFA算法求解问题。
【代码实现】
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 20005;
const int maxm = 40005;
int n, m;
struct Edge {
int next;
int to;
int dis;
} edge[maxm];
int head[maxn], _count;
void add_edge(int from, int to, int dis) {
edge[++_count].next = head[from];
head[from] = _count;
edge[_count].to = to;
edge[_count].dis = dis;
}
long long dis[maxn];
int mark[maxn];
void spfa(int start) {
memset(dis, 0x3f, sizeof(dis));
memset(mark, 0, sizeof(mark));
queueque;
que.push(start);
mark[start] = 1;
dis[start] = 0;
//不存在负权回路
while (!que.empty()) {
int u = que.front();
que.pop();
mark[u] = 0;
int k = head[u];
while (k != 0) {
int v = edge[k].to;
int u_v = edge[k].dis;
if (dis[v] > dis[u] + u_v) {
dis[v] = dis[u] + u_v; //update dis
if (mark[v] == 0) {
que.push(v);
mark[v] = 1;
}
}
k = edge[k].next;
}
}
}
int main() {
//input data
//clock_t s = clock();
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add_edge(x, y, z);
// add_edge(y, x, z);
}
spfa(1);
cout << dis[n];
//output time
//cout < 1420:Dijkastra(II)
【题目描述】
给定一个无向连通图,求从1到n的最短路。
【题目分析】
使用优化的dijstra算法进行求解
【代码实现】
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;
const int maxm = 400005;
int n, m;
struct Edge {
int next;
int to;
int dis;
} edge[maxm * 2];
int head[maxn], _count;
void add_edge(int from, int to, int dis) {
edge[++_count].next = head[from];
head[from] = _count;
edge[_count].to = to;
edge[_count].dis = dis;
}
long long dis[maxn];
int mark[maxn];
priority_queue> q; //大根堆,将dis取反即可得到小根堆
void Dijkstra(int start) {
//init dis and book
memset(dis, 0x3f, sizeof(dis));
memset(mark, 0, sizeof(mark));
//init dijkstra
dis[start] = 0;
q.push(make_pair(0, start));
while (q.size()) {
int u = q.top().second;
q.pop();
if (mark[u]) continue;
mark[u] = 1;
int k = head[u];
while (k != 0) {
int v = edge[k].to;
int u_v = edge[k].dis;
if (dis[v] > dis[u] + u_v) {
dis[v] = dis[u] + u_v;
q.push(make_pair(-dis[v], v));
}
k = edge[k].next;
}
}
}
int main() {
//input data
//clock_t s = clock();
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add_edge(x, y, z);
add_edge(y, x, z);
}
Dijkstra(1);
cout << dis[n];
//output time
//cout < 1421:Floyd
【题目描述】
给定一个n个点m条边的有向图。Dis(a,b)表示a到b的最短距离,如果a无法到b,则Dis(a,b)=10^16,规定 Dis(a,a)=0。
读懂以下程序,并输出S。
【题目分析】
^表示二进制异或操作
根据数据范围定义long long 的邻接矩阵,使用Floyed算法求解任意两点之间的最短距离,S=0,f=1e16 根据题目要求计算S异或任意两点的最短距离+f的数值,数值不会超过1e16的范围,long long的数据范围为1e18.
【代码实现】
#include
using namespace std;
int n, m;
long long dist[550][550];
void floyd() { //floyd算法
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (dist[i][k] != 1e16 && dist[k][j] != 1e16) {
dist[i][j] = min(dist[i][k] + dist[k][j], dist[i][j]);
}
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dist[i][j] = 1e16;
}
}
for (int i = 1; i <= n; i++) {
dist[i][i] = 0;
}
for (int i = 1; i <= m; i++) {
long long u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
dist[u][v] = min(w, dist[u][v]);
}
floyd();
long long S = 0, f = 1e16;
for (int i = 1; i <= n; i++) {
for (int j = 1 ; j <= n; j++) {
S ^= dist[i][j] + f;
}
}
cout << S << endl;
return 0;
}