dfs主要思路:
从一个节点出发,遍历与该节点相连的所有点,有时不给重复访问,标记设置一次即可,动态规划中,有时需要dfs遍历标点的记号;有时又求不同路径总数,需要先标记再撤去标记,恢复现场,不影响其他搜索。当然,和所有递归一样,这是要有边界的,不能无限递归下去,边界一般根据题目获得。dfs是最朴素的暴力解法,找极大连通子图(如果标记的话)个数,等等,暴力选dfs
bfs主要思路:
从一个节点出发,一层一层扫,找到的路径就是最短路径,那怎么记录最短路径走的步数,可以使用一个数组step,step[i]记录走到队列中第i个状态i的步数,每次从队中出队一个元素,并将该元素相连的点(没有被遍历)加入到队列中,同时记录加入点的步数(队列最后一个元素位置编号是v.size()-1,那么step[v.size()-1] = step[i]+1;),循环即可使用bfs,队列就用vector也可以,STL性价比不是很高。
20220405补充,bfs中,一般将步数最短路径信息连同节点坐标信息(如果必要的话)存储在一个结构体中,完毕。
如图所示: 有9只盘子,排成1个圆圈。其中8只盘子内装着8只蚱蜢,有一个是空盘。
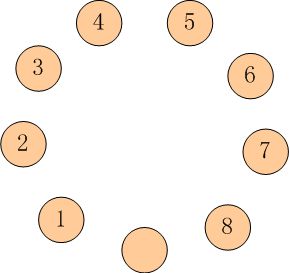
我们把这些蚱蜢顺时针编号为 1~8。每只蚱蜢都可以跳到相邻的空盘中,也可以再用点力,越过一个相邻的蚱蜢跳到空盘中。
请你计算一下,如果要使得蚱蜢们的队形改为按照逆时针排列,并且保持空盘的位置不变(也就是1-8换位,2-7换位,...),至少要经过多少次跳跃?
小思路:
蚂蚱动是不是很好编程实现的,换个角度,我们让空盘子动,循环队列,邻接表存在那,不需要存,直到某个状态与下个状态的关联(连接的关系即可)
让空盘子动,和8数码问题类似。
#include
#include
#include
#include
#include
#include
#include
该代码全部自己调试,未参考其他代码,注意怎么存储步数
方格计数
6x6的方格,沿着格子的边线剪开成两部分。要求这两部分的形状完全相同。如图就是可行的分割法。
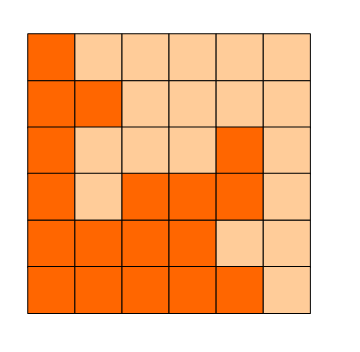
试计算:包括这3种分法在内,一共有多少种不同的分割方法。注意:旋转对称的属于同一种分割法。
对称中心点,dfs,注意,要双向,就是每次走,都是对称走,如一端向上,则另一个端同时向下,由于中心对称,一端至(nextx,nexty)时,另一端直接对称,就是(对称中心x*2-nextx,对称中心y*2-nexty)
#include
#include
#include
#include
#include
#include
#include
![]()
