可能你已经刷了很多01背包的题，但是真的对01背包领悟透彻了吗？，看我这一篇，使君对01背包的理解更进一步【代码+图解+文字描述】

一.概念理解：什么是01背包

关于01背包的概念理解如下：01背包是在M件物品取出若干件放在空间为W的背包里，每件物品的体积为W1，W2至Wn，与之相对应的价值为P1,P2至Pn。001背包的约束条件是给定几种物品，每种物品有且只有一个，并且有权值和体积两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。

二.大多数人对01背包理解不够透彻的原因

关于为什么大多数人对01背包理解不够透彻呢，我们从以下两个角度进行分析：

①01背包问题的代码相对而言比较简短，但是理解起来却没那么容易，这也就导致了很多同志直接萌生了背代码的应对策略，当遇见01背包的问题时直接套代码，感觉这样既省时又省力，但是一旦对01背包的问题进行一小部分的改动，马上就被打回原型了~

②即使理解了01背包的规划策略，但是还是对01背包所创建的数组和数组下标的含义有所模糊，甚至可能当AC了01背包的题目，都不知道01背包的dp数组具体的含义

三.01背包的理论策略（暴力递归）

其实对01背包的分析我们可以将其理解为背包容量和物品的价值和对应的重量的分析：对于每一个物品而言，我们都有将其放入背包和不放入背包两种选择，我们按照物品的顺序从前到后进行策略的选择，无论当前物品是否放入背包，我们都必须要保证一个结果，当我们在处理完最后一个物品的放和不放的决策之后，物品和的总重量必须不大于背包的总容量，至于所说的背包所能容纳的最大价值，我们只需要在每次做完最后一后一个物品的决策之后，选择符合要求的最大价值进行返回即可。而至于在策略途中某个物品的加入使得总物品的重量和超过了背包的总容量，我们直接将这种策略终止即可，而这种理论策略，恰好是背包问题的暴力递归实现的思路，我们选择趁热打铁，直接将关于01背包问题的暴力递归代码（附注释）奉上：
 

public class Bag {
    public static void main(String[] args) {
        int[]w={3,4,5};
        int[]v={6,4,8};
        System.out.println(bestBag(w, v, 10));
    }
    public static int bestBag(int []w,int []v,int weight){
        //检查有效性
        if(w.length==1&&w[0]>weight){
            return 0;
        }
       return process(w,v,0,0,weight);
    }
    //递归过程

    /**
     * 
     * @param w 物品的重量数组
     * @param v 物品的价值数组
     * @param index 遍历的当前物品的序号
     * @param alWeight 当前所遍历过的物品中在选择放与不放之后的重量
     * @param weight 背包的容量
     * @return
     */
    private static int process(int[] w, int[] v, int index, int alWeight, int weight) {
        //判断出口
        if(alWeight>weight){
            return -1;
        }
        if(index==w.length){
            return 0;//成功
        }
        //第一种情况：当前节点上不放值(因为当前物品一旦加入到背包中，背包的总容量就超了)
        int value1=process(w, v, index+1, alWeight, weight);
        //第二种情况：当前结点放入值
        int value2Next=process(w, v, index+1, alWeight+w[index], weight);
        int value2=-1;
        if(value2Next!=-1){
            value2=value2Next+v[index];
        }
        //返回两种结果的最大值
        return Math.max(value1, value2);
    }
}

四.关于01背包实现的动态规划策略

4.1使用二维数组实现01背包的动态规划

关于动态规划问题，我进行实现和分析的策略是将其分为五部分：①递归数组元素的下标以及元素的含义②递推方程的实现③dp数组的初始化④dp数组的遍历顺序⑤在出现错误时，我们通过打印dp数组的方式快速准确的定位问题出现的所在，提高debug的效率

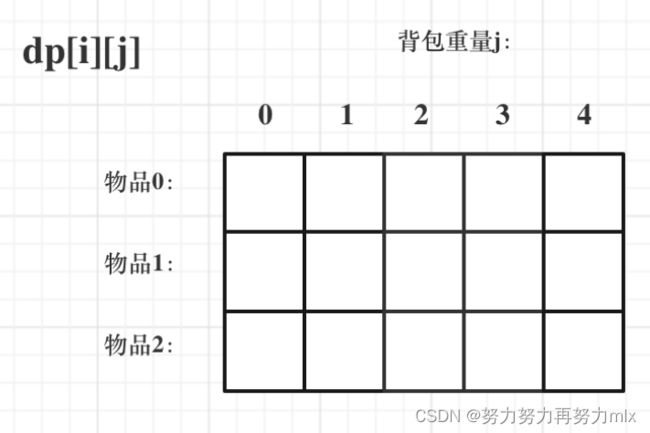
对于01背包问题的分析，我们从这五个方面进行分析：①我们创建二维的dp数组,举例dp数组中的一个元素为dp[i][j],i代表遍历的当前物品，j代表当前dp数组的容量（这样的话我们默认先遍历物品再遍历容量（一层循环是对物品的遍历，二层循环是对容量的遍历），其实反过来遍历也可以，我们后面再进行解释~），dp[i][j]中的具体数值则代表对于当前i个物品的选择中，能够满足j容量的最大价值

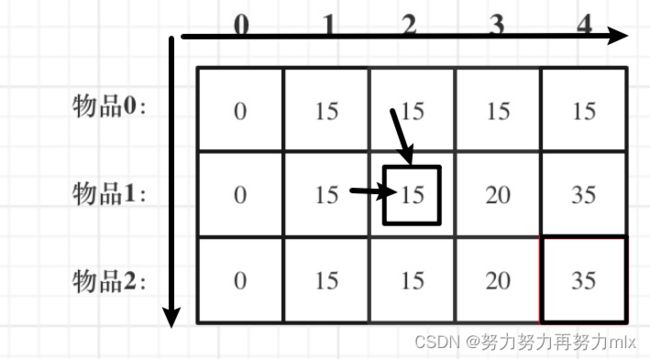
②递推公式：我们对01背包的问题进行分析:我们要想实现使得背包容量能取最大值，那么我们一定要使背包的容量尽可能的被占满，且能在当前能够选择的所有物品中进行选择，所以当我们面对每一个物品进行选择时，当要对当前的能选择的全部物品，且尽可能使用所有的背包的剩余容量，结合上面我们所说的dp[i][j]的含义是当前j容量下对当前前i个物品进行选择时，所能容纳下的最大价值，所以dp[i][j]的递推公式应该是由当前物品的选和不选的策略中取其最优解：dp[i][j]=max(dp[i-1][j],dp[i][j-weight[i]]+value[i]),我们对这个递推公式进行解释：dp[i-1][j]的含义我们不选择当前的这个物品，所以我们只对i-1个物品中进行选择，因为不需要考虑当前物品对背包容量的影响，所以对于背包容量的选择，我们选择当前所能选择的最大背包容量j;dp[i][j-weight[i]]+value[i]:这个是我们选择当前的物品放入背包，既然把当前物品放入背包，那么在放入这个物品后，所能容纳的最大容量只剩下【j-weight[i]】了，所以我们在前i-1个物品中在容量为j-weight[i]的情况下选择其最优解，然后将最后物品的价值加入即可。与此同时，我们对前面说到的关于先遍历物品还是先遍历背包容量的问题进行说明：我们先把结论摆在这：都可以，为什么呢？我们观察以下的图片结合递推公式我们可以发现，对于每一个元素，都是由当前元素右边的某个元素和当前元素上面的元素共同推出，所以不论先遍历物品还是先遍历遍历容量，我们都要满足该元素的右边元素和上边元素都被求出来了，但是先遍历容量（相对于按列遍历）还是先遍历物品（按行遍历），其右边和上边的元素都被遍历完成了，所以这两种遍历方式都可以

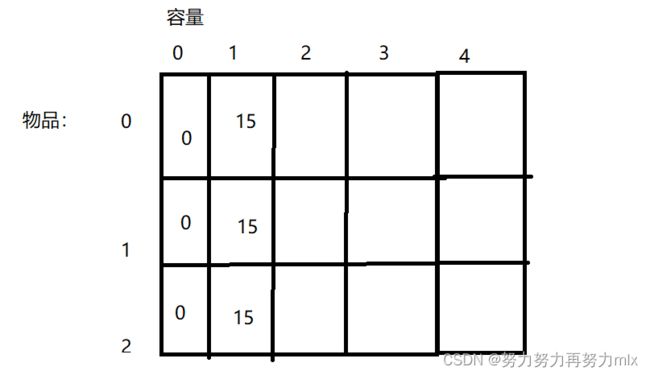
③初始化：（我们仍然结合上图）对于容量为0的情况下，任凭有再多的物品，我们仍然一个物品都放不下：多以对于第一列的数据，我们将其初始化为0，对于只有物品0的情况下，如果我们当前背包的容量能够大于等于该物品的重量，我们能将物品的价值放入数组，但是如果当前背包的容量小于这个物品的重量，这种背包情况下的数值仍然是0，而其他没有涉及到的行列值呢？我们由递推公式可以得到：当前行列中元素的值与当前这个元素并没有任何关系，而是由其上边和左边元素共同决定的，所以对于这些元素的初始化任何值都可以，我们选择其一，将其初始化为0

④遍历顺序：既然所有的元素都是其上边和左边元素共同推出来的话，所以我们元素的遍历顺序应该选择从上到下，从左到右进行遍历。

⑤打印数组：如果我们发现最后的结果不正确，我们可以从头到尾将数组打印一遍，快速定位错误。

code【代码+注释】如下：
 

/**
 * @author tongchen
 * @create 2023-04-13 15:26
 */
public class DpBag {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        MostWeightDpBag(weight, value, 4);

    }

    /**
     * 五部曲：1.dp[i][j] dp[i]是在0-i内存放东西的策略 j是背包容量为j,则dp[i][j]可以理解为在0-i的物品内和容量为j的背包所能存放的最大容量
     * 2.递推方程：dp[i][j]=math.max(dp[i-1][j],dp[i-1][j-w[i]])3.初始化当背包容量为0时，每一个i都是0，当物品为i时，每个背包能存放的最大价值为i
     * @param
     * @return
     */
    public static void MostWeightDpBag(int[]weight,int []value,int maxSize){
        //创建数组
        int[][]dp=new int[weight.length][maxSize+1];
        //初始化
        for(int i=weight[0];i<=maxSize;++i){
            dp[0][i]=value[0];
        }
        //循环
        //一层循环物品
        for(int i=1;i< weight.length;++i){
            //二层循环背包
            for(int j=1;j<=maxSize;++j){
                dp[i][j]=dp[i-1][j];
                if(weight[i]<=j){
                    dp[i][j]=Math.max(dp[i][j],dp[i][j-weight[i]]+value[i]);
                }
            }
        }
        for (int i = 0; i < weight.length; i++) {
            for (int j = 0; j <= maxSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}

4.2使用一维数组实现01背包的动态规划（滚动数组）

4.2.1从二维数组到一维数组的变化

在讲解真正的从二维数组降解到一维数组之前，我们先看一下从二维数组到一维数组的变化：从二维数组降解到一维数组，显著的变化是我们取消了对物品i的区别，只有j这一个一维数组的下标，代表j容量下所能容纳的最大价值，最本质的原因是将dp[i-1][j]这个元素直接拷贝到了dp[i][j]；除此之外我们再来分析其他的变化：①遍历顺序不再什么都可以，而是必须先遍历物品，再遍历容量，对于容量的遍历，我们必须采取容量从大到小的遍历方式②关于初始化：初始化元素的定义因为不再是从上一行的元素进行拷贝，而是在选择（dp[j]）和不选择当前物品放入背包(dp[j-weight[i]]+value[i])进行考虑,取其最大值，所以在两者的比较过程中，我们不能使我们的初始化对其产生影响，而dp[j]的含义仍然是在j的容量下，背包所能承受的最大价值，所以初始化不能是负数，也不能对比较产生影响，所以我们将其初始化为0（最小的非负数）

4.2.2对问题重新进行分析以及对二维数组到一维数组变化的难点分析

我们首先进行问题的分析：
我们依然从①递归数组元素的下标以及元素的含义②递推方程的实现③dp数组的初始化④dp数组的遍历顺序⑤在出现错误时，我们通过打印dp数组的方式快速准确的定位问题出现的所在，提高debug的效率这五部分进行分析：

①dp[j]代表j容量下背包所能容纳的物品的最大价值 ，j代表背包的容量

②由于是将不选择当前物品的情况（将i-1的元素直接落到i）,所以我们的递推公式还是从选择和不选择当前物品中选取最大值：dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j],此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，所以递推公式为：dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);

③初始化：dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);dp数组在推导的时候一定是取价值最大的数，初始化的值为背包所能承受的最大价值，所以初始化不能是负数，也不能对比较产生影响，所以我们将其初始化为0（最小的非负数）。

④遍历顺序：与二维数组不同的是，一位数组中我们必须先遍历物品，再去遍历容量，且容量必须从后往前遍历（容量从大到小遍历）：可能这时候同志们就有疑惑了：为什么不能先遍历容量呢？为什么对容量的遍历不能从前往后呢（容量从大到小），我们依次进行解答：①如果是先遍历容量相当于将数组进行列的遍历，（按照一列一列的顺序进行遍历），我们一定要保证的是当前为j的容量所能容纳的最大值是正确的，那么其选择和不选择当前物品放入背包对应的值也应该是正确的：我们以以下图片的背包进行分析：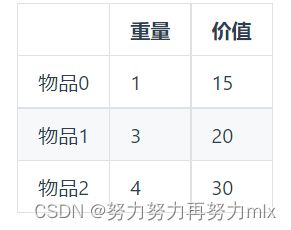

如果是按照列进行遍历，其实是违反当前容量所能容纳最大值策略这个原则的：为什么这么说呢？因为如果按照列进行遍历，我们将情景带回到二维数组，相当于是将上一行的元素直接进行了复制，这样也就违反了我们每一个元素其实代表着当前容量下所能容纳的最大价值的物品。

如果大家觉得还是有些抽象的话，大家可以将数组中的元素打印一遍，然后查验一下结果和思路 。

再讲一下为什么关于容量的遍历为什么要从大到小进行遍历呢？因为如果是从小到大进行遍历，会导致同一个物品重复放置：

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历dp[1] = dp[1 - weight[0]] + value[0] = 15dp[2] = dp[2 - weight[0]] + value[0] = 30此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历；为什么倒序遍历，就可以保证物品只放入一次呢？倒序就是先算dp[2]dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）dp[1] = dp[1 - weight[0]] + value[0] = 15所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。如果大家还是有所疑惑，建议大家将数组打印一遍，去梳理一下整个遍历的过程。

根据这样，我们给出code：

/**
 * @author tongchen
 * @create 2023-04-14 18:00
 */
public class RollingDpBag {
    public static void main(String[] args) {

    }

    /**
     * 1.j代表容量为j2.dp[j]代表j容量下存放的最大值2.dp[j]=max(dp[j],dp[j-weight[i]]+value[i])3.dp[i]=0;4.第一层是物品，从上到下，第二层是容量，从左到右
     */
    public static void dpBag(int[]weight,int []value,int maxSize){
        int[]dp=new int[maxSize+1];
        for(int i=0;i< weight.length;++i){
            for(int j=maxSize;j>=weight[i];--j){
                dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
            }
        }


    }
}