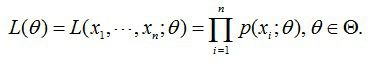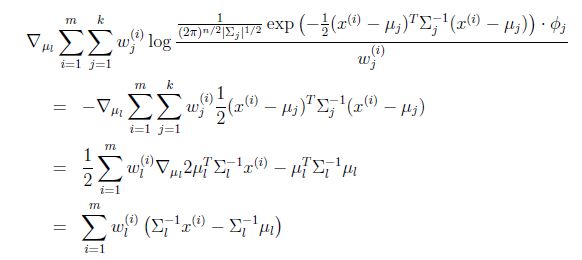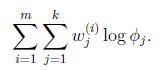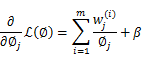利用EM算法对高斯混合模型GMM进行求解

• 高斯混合模型      

 高斯混合算法GMM和大家比较熟悉的k-Means算法同属聚类算法的一种。在分类或者搜索算法中，我们对一些样本进行聚类后可以对新的数据进行分类。对于k-means算法来讲结果就是一个固定值（是哪一类就是哪一类），而对于GMM算法的结果是一种概率值（属于哪一类的概率是多少）。无论对机器还是人来说，对一个事情进行结果判定，给出概率值要比给出固定值（绝对）要好多的，或者说是结果更加严谨。举个例子就比较容易理解了，对一个病人的病情进行判断，如果这个人的状况表现为发烧和喉咙疼，我们百分之九十概率来判断说该病人是感冒的结论要比百分之百是感冒的话要严谨的多。乍一看没什么，但是如果一种病情的结论是百分之四十九为绝症而百分之五十一为普通小毛病怎么办。所以说，我们可以通过概率的方式来决定是否对病人进一步的检查或判定病情。说了那么多，GMM到底是什么东西？其实我们可以假设一堆数据是服从GMM分布的，或者说我们这些数据是由GMM分布随机选出来的（1）。由其名字也可以推算出它是由多个权重不同的单个的高斯分布组成的；比如说一堆人里面由小孩和大人组成，我们可以通过身高来对判断一个人是属于哪一类。我们知道，对于小孩和大人都可以利用高斯分布来进行表示，只是小孩和大人的高斯分布函数中的两个未知量（均值和方差）不同。但是如果把小孩和大人混合在一起，那么这堆由大人和小孩的组成的人群该通过什么概率分布函数来表示呢？一方面可以通过脑补猜到这个概率分布函数可能（假设为GMM）是一个驼峰形式的函数（由两个单个但是不同权重的高斯分布函数相加得到），只是难点在于如何确定该函数中的每个高斯分布的方差、均值以及权重这三个未知数（2）。其实我们可以通过任意的分布来组成某某混合模型（XX  Mixture Model），但是GMM还是最为流行，并且他可以变得任意复杂从而可以逼近任何连续分布的概率密度函数。对于k-means聚类，聚成类的数量为K，而GMM聚成类别的数目也同样为K，K表示多少个单个高斯分布函数。我们通过下面这个公式来确定GMM的概率密度表示形式为：                           

                                                                               公式（一）

其中 为（或者称为component）系数，同P(k)，和为1， 和  分别为均值和方差，。如果我们随机从该分布中取一个点的话，可以先确定这个点是由第k（k = 1，2.....K）个单独的高斯分布函数的概率（就是系数），然后再确定该高斯分布的 和  （3）。这就转化为了求解普通的高斯分布函数了。以上介绍了混合高斯模型为何物以及求解的大体流程。我用黑粗字体标记了三句话，在下面对GMM的参数进行详细求解的流程中，都是围绕着这三句话来进行解释的。

在正式进行高斯模型求解之前，说一下自己对高斯混合模型的看法。首先从kmean's算法的角度来看，这个算法确实很惊艳，因为它给出了一个样本属于哪个类别的概率而不是确定。再则就是，对于该模型的具体用法和表达意义：我们知道，高斯混合模型它终究是一个概率预测模型，为什么能做到分类呢？假设我有两堆分类，分别在x轴远点左边和右边，并且这类数据完全对称，均值分别在-2和2，方差很小，表示着驼峰很尖。P = a1*p1 + a2*p2，既然完全对称，那么a1 = a2 = 0.5。假设通过这个模型产生一个值为2+左右的粒子，其概率还是很大的。逼近极限的话p2为1（我这里不知道表达准不准确，因为对于概率密度而言，求概率的过程是对概率密度积分，而积分对一个点来讲是没有意义的，为了严谨，该值为2+，表示2左右的一小段），然后乘以系数a2为0.5，但是p1值就很小了，忽略。总之，我们可以称该模型生成粒子为2+的概率为0.5。但是假如想要生成为0+的粒子的话，该模型生成的概率就很低。上面的逻辑也可以这样想，如果粒子在2和-2左右，这些粒子都很普通，通过将该粒子表示的数带入该混合高斯模型（GMM）的p1部分和p2部分，可以求出p1和p2的值，比较p1和p2的值的大小，从而确定该粒子属于哪一类。但是如果将0带入该模型，p1和p2的值都很小，两者相差也不明显，这样可以一方面认为不太好确定属于哪一类，另一方面也说明该粒子0+发生的概率本来就很小。所以说，单单的看，将单个粒子带入GMM模型产生的概率值是没有意义的，他不像单个高斯模型产生的意义（比如说，人类的身高平均在1.7，如果一个人为1.75，表示这个人的身高很普通，因为概率发生的很大，但是如果一个人的身高为3米，则概率值就很小，可以认为是身高界的奇葩）。但是对于分类，新的粒子分别带入单个高斯模型并计算出相应的概率值，比较概率值的大小确定类别。说了这么多，只是想表达一个意思：公式（一）中的在GMM用于分类过程中是没有任何意义，它的意义为：GMM的最大似然估计求解过程用到以及生成某一个粒子时的概率（比如说粒子2+，而生成粒子的概率对于分类来讲没有任何意义，但是如果一个粒子对于GMM来讲，他的概率很小，则该粒子很有可能他不属于任何类别，或者说属于任何一个类别的概率都很小）。

• 高斯混合模型参数求解

整个高斯混合模型的参数求解涉及到的知识点可以分为两个：最大似然估计和EM算法。

1.最大似然估计

先举一个比较常见的例子，假如一个框里有十个球，八个黑球，两个白球。我们说从框里取出一个黑球的概率是多少，答案很明显就是0.8。但是这个数字怎么来的，其实是根据前人总结的经验得来。但是如果我们事先不知道框里有多少黑球和白球，但是我们有放回（有放回后，表示每次取球的时间都是独立的）的取了几次球后，知道取了黑球和白球被取出的次数后也可以根据“感觉”来得出答案，比如说取了十次有八次黑球，两次白球，我们凭“感觉”为0.8。但是这个结论如何通过严禁的数学来证明呢？或许说，如果对于一个复杂的概率分布模型（比如说高斯分布）我们不能一下子凭直觉计算出答案。这种知道了概率分布模型（或概率密度函数），但是不知道模型中的具体参数，我们要做的是求出参数是参数估计。常用的方法有距估计（具体的距估计方法本不做介绍）和最大似然估计。

      回到取球的事件，我们可以假设取出黑球的概率为P，那么取出白球的概率为1-P。我们有放回的取了十次球这个独立事件可以表示为F = P^8(1-P)^2，求最大似然估计也就是意味着使"取了十次球后这个事件"发生，概率P的值最大。极值的出现一般在于导数为0时。那么我们对P^8(1-P)^2求导后令其为0，得出（5P -1）*(P-1) = 0,得出P = 0.8。

求最大似然函数估计值的一般步骤：

　　首先，写出似然函数：

　　　　　　　　

　　其次，由于通常单个事件发生的概率都很小，许多很小的数字相乘起来在计算机里很容易造成浮点数下溢，因此可以对似然函数取对数，并整理：

　　　　　　　　

　　然后，求导数，令导数为0，得到似然方程；最后，解似然方程，得到的参数即为所求。

在了解了何为最大似然估计后我们回到高斯混合模型，还是那个例子，一堆人里面有小孩和大人，这样的模型该如何表示呢。在解释GMM中说过这么一句话：其实我们可以假设一堆数据是服从GMM分布的，或者说我们这些数据是由GMM分布随机选出来的（1）。如果我们知道该GMM分布的所有参数，那么这么一堆人（结果）可以通过这个GMM分布得出；同样，我们现在知道了有这么一堆人（结果），但是我们知道这个是符合GMM分布的，但是不知道具体参数，这很明显就是参数估计问题。那么求解方法可以利用最大似然估计。

那么GMM的似然估计函数可以写成：

                                                                      公式二

由于参考了多个博客，这里log等于上式中的ln，N表示这样本个数，K代表着GMM是有K个单个高斯模型构成。我们的任务就是求解 、 和  。他们三个代表的意思已经解释过。但是我们也注意到了该式在对数里面又有加和操作，求导展开的难度难以想象，所以我们没有办法直接用求导解方程的办法直接求得最大值。由此引出了Jensen不等式和EM最大期望算法。

2.Jensen不等式

1）定义

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。  Jensen不等式表述如下：      如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])  。当且仅当X是常量时，上式取等号。

2）举例

图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。Jensen不等式应用于凹函数时，不等号方向反向。当公式取等号时，f（X）为常数C。对于凸函数和凹函数的定义，国内外的标准不一样，所以参考的文献不一样可能结论是恰恰相反的，我们只需理解是相应的意思就好。或者说根本就没有凹函数一说，只有上凸和下凸函数。

3.EM(Expectation Maximization)期望最大算法

      我们先对EM算法的模型以及推到过程做一个简单的分析，详细的求解过程在GMM参数估计求解中在具体体现，之所以不复杂的介绍求解过程，主要是想体现这种巧妙的转换思想有多么的厉害：利用log这种凸函数性质、结合期望公式中的Lazy Statistician规则将我们上面提到的问题，即log函数中有‘加和’操作而导致求导过程异常复杂的问题变成log函数只有乘除这种简单求导过程。

     所谓的 Lazy Statistician规则为：      

设 Y是随机变量X的函数，即Y = g（X),如果g（X）是连续函数，那么分为两种情况：         （1） X是离散型随机变量，它的分布律为，k=1,2,…。若绝对收敛，则有              （2） X是连续型随机变量，它的概率密度为，若绝对收敛，则有

该图引用别的文章，简单来说就是：如果求随机变量X的期望，那么就是E[X]，  如果求函数Y（X）的期望就是E[Y(X)],如果某某的期望就是E(某某），为了方便理解，我们暂不纠结这种叫法是否正确。

模型说明：

    考虑一个参数估计问题，现有 y1,y2,…,yn共 n 个独立训练样本，需有多个参数 π 去拟合数据，那么这个 log 似然函数是：

 

                                          

  在GMM中P就是模型的概率分布，我们在上边以上说过了，直接对θ（在这里为K个方差、均值和权重）求导过于复杂，那么这时我们需要加入一个隐藏变量 z，以达到简化 l(θ)，迭代求解 l(θ) 极大似然估计的目的。

算法推导：

加入的隐形变量z，那么Q（z）表示为隐形变量Z的某种分布，可以想象成通过调整Q（z)的参数，使得每个粒子属于某一类别的概率较大，从而使得P(Y,Z)最大。由于加入了隐形变量，则可以由上式变化和推到如下：

                                        

      这个三步的变化就是整个EM算法的精华，第一行中仅为加了隐形变量后写法的变化。可以不成文的想象成：P的模型对于样本来说不再是一层不变（因为假如把P看成无未知量的概率分布，输入一个样本值，该样本属于某一类别的概率值就出来了，但是现加入了隐形变量，意味着通过调整该隐形变量，可以调整样本属于某一类别发生的概率值。因此可以想象成权值。这里所说的类别就是一个高斯模型）。第二行中也同样比较容易理解，分支分母都乘以Q(Z)。关键是第二步到第三步的转变，我们通过Jensen不等式可以把E[f(X)]和f(E[X])的关系连起来。我们有知道log是个上凸函数，可知道f(E[X])>=E[f(X)]，从上面Lazy Statistician规则可知，X不一定就是随机变量，他也可能是一个随机变量函数Y。在这里，这个随机变量函数Y(相当于介绍Lazy Statistician时表格中的g)：，随机变量为Z，概率分布Q(Z)相当于表格中的p。或许有人问，那方程中的方差和均值呢？需要说明的是，我们利用这个公式进行求解的是隐形变量Z，其他的变量是假设成已知的。所以这里主要是对随机变量函数Y求期望。所以f(E[X])>=E[f(X)]中，E[X] = ，f(E[X]) = log(E[X])=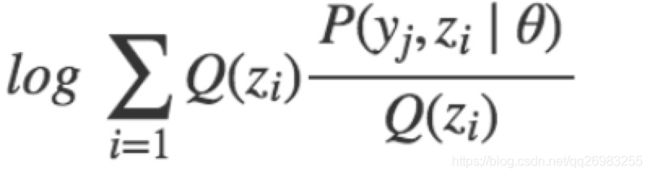。E[f(X)]中f(X)=，所以E[f(X)] = 。上面中的X代表的意思，有时候是随机变量，有时候又是随机变量函数。可能存在表述不严谨。主要是想表达 Lazy Statistician规则中对随机变量函数求期望的思想转换。

       由此，根据Jensen不等式可知，两公式相等的条件为P=C：

这样就可以求出zi的值，然后假设方差和均值变成未知量，通过最大期望可以更新先前假设方差和均值为已知量的值。这样有可以求出新的zi，如此循环下去。

        

参考的博客中，有人画出相应的图形变化，感觉对理解还是有帮助的。

4. GMM求解

通过上次分析可知，EM算法就是围绕第二句话： 如何确定该函数中的每个高斯分布的方差、均值以及权重这三个未知数（2）。            在理解GMM算法之前，结合自身对该算法的理解过程，感觉还是和K-mean算法的某些思想有些相似的。比如说，需要假设未知数已知的设想。假设将一堆数据（粒子）分为五类，在k-means算法中，第一步：我们需要随机选取五个点来作为每一类的基准，学名为均值向量，即第一轮循环下来，所有数据被分到这五个粒子的队伍。被分为某一个类的标准就是：把每个粒子与五个基准粒子做距离计算di（i=1，2，3，4，5），那么五个长度肯定有一个最短距离dt，dt是和第几个基准粒子的长度，该粒子就属于哪一类；最后所有的粒子都有了归属，我们需要更新基准粒子了。第二步：假设取第一类，我们需要计算所有粒子的质心点在哪里，（每一个粒子表示为一个向量，将该类里面的所有粒子求和作平均），由于做了平均，那么该基准粒子就可能不再是一个实际存在的粒子了，仅仅是代表的一个位置。然后重复上述过程，最后基准粒子（均指向量）不再变化，类就分好了。

     那么类似k-mean聚类方法，假设GMM是有五个单高斯分布组成，即分为五类。k-mean算法中，我们选取了五个样本（在GMM中，由于涉及到了统计学，我们把粒子比喻成样本）作为基准。

GMM参数估计求解过程：这里盗用该博客的推到过程，叙述的非常清晰明了，其中加了一些解释：

我们已经知道了EM的精髓和推导过程，再次审视一下混合高斯模型。之前提到的混合高斯模型的参数和计算公式都是根据很多假定得出的，有些没有说明来由，为单个高斯分布的权重，初始化可以为1/k，表示每个高斯分布权重相同。为了简单，这里在M步只给出和的推导方法。

E步很简单，按照一般EM公式得到：

      

      简单解释就是每个样例i的隐含类别为j的概率可以通过后验概率计算得到。

      在M步中，我们需要在固定后最大化最大似然估计，也就是

      

      这是将的k种情况展开后的样子，未知参数和。

      固定和，对求导得

      

      等于0时，得到

      

      这就是我们之前模型中的的更新公式。

      然后推导的更新公式。看之前得到的

      

      在和确定后，分子上面的一串都是常数了，实际上需要优化的公式是：

      

      需要知道的是，还需要满足一定的约束条件就是。

      这个优化问题我们很熟悉了，直接构造拉格朗日乘子。

      

      还有一点就是，但这一点会在得到的公式里自动满足。

      求导得，

      

      等于0，得到

      

      也就是说再次使用，得到

      

      这样就神奇地得到了。

      那么就顺势得到M步中的更新公式：

      

      的推导也类似，不过稍微复杂一些，毕竟是矩阵。结果在之前的混合高斯模型中已经给出。

参考：

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html#!comments

https://www.cnblogs.com/mindpuzzle/p/3659444.html

https://www.cnblogs.com/mindpuzzle/p/3730534.html

https://www.cnblogs.com/Gabby/p/5344658.html