Greedy Gradient Ensemble for Robust Visual Question Answering论文笔记
Greedy Gradient Ensemble for Robust Visual Question Answering 论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
-
- 3.1 Debias with dataset construction
- 3.2 Debias with model design
- 四、Revisiting Language Bias in VQA
-
- 4.1 问题定义
- 4.2 Experimental Analysis for Language Bias
-
- 4.2.1 Inverse Grounding Annotation
- 4.2.2 Vision-only Model
- 4.2.3 Inverse Supervision for Balanced Classifier
- 五、方法
-
- 5.1 Greedy Gradient Ensemble
- 5.2 GGE Implementation for Robust VQA
-
- 5.2.1 Distribution Bias
- 5.2.2 Shortcut Bias
- 5.2.3 GGE-D
- 5.2.4 GGE-Q
- 5.2.5 GGE-DQ
- 5.3 Connection to Boosting
- 六、实验
-
- 6.1 评估指标
- 6.2 Comparison with State-of-the-art Methods
- 6.3 Ablation Studies
- 6.4 Generalization of GGE
-
- 6.4.1 Self-Ensemble
- 6.4.2 Generalization for Loss Function
- 6.4.3 Generalization for Base Model
- 6.5 Qualitative Evaluation
- 七、 结论
- 八、补充材料
- 写在最后
写在前面
很长一段时间没写博客了,时间真是太紧了,好好学习~
分享一篇ICCV2021的文章,关于VQA中的bias,评价数据集为VQA-CP-v2和VQA-v2
论文地址:Greedy Gradient Ensemble for Robust Visual Question Answering
代码地址:GitHub
一、Abstract
VQA模型在没有考虑图像信息的情况下,总是会基于语言bias进行预测。本文提出VQA模型中语言bias主要来源两个方面:
1、数据集的分布bias
2、捷径bias
进一步提出来一个新的de-bias框架,Greedy Gradient Ensemble (GGE),可以联合多种有bias的模型来学到无bias的模型。
理论依据:采用贪心策略,强迫有bias的模型在一开始就过度拟合bias的数据,因此base模型能够去关注那些bias模型无法解决的样本问题。
二、引言
大多的VQA方法往往依赖于数据集中的bias,即没有考虑到图像中视觉信息的情况下,总是会利用问题和答案之间的表面联系来回答问题。
例如,当问到“what sports”时,模型可能盲目的回答“tennis”,因为训练集中大多数的QA对都是这个。因此,模型在这样的数据集中训练之后便很难回答其他的问题(即使图像有很大不同)。
当前解决这种bias问题的方法可大致分为三种类型:
1、基于ensemble-based的方法
[38] Sainandan Ramakrishnan, Aishwarya Agrawal, and Stefan Lee. Overcoming language priors in visual question answering with adversarial regularization. In Advances in Neural Information Processing Systems, pages 1541–1551, 2018. 1, 2, 6
[7] Remi Cadene, Corentin Dancette, Matthieu Cord, Devi Parikh, et al. Rubi: Reducing unimodal biases for visual question answering. In Advances in neural information processing systems, pages 841–852, 2019. 1, 2, 3, 4, 6, 7, 12, 13, 14
[10] Christopher Clark, Mark Yatskar, and Luke Zettlemoyer. Don’t take the easy way out: Ensemble based methods for avoiding known dataset biases. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, pages 4060–4073, 2019. 1, 2, 3, 6, 7, 12, 13, 14
2、基于grounding-based的方法
[43] Ramprasaath R Selvaraju, Stefan Lee, Yilin Shen, Hongxia Jin, Shalini Ghosh, Larry Heck, Dhruv Batra, and Devi Parikh. Taking a hint: Leveraging explanations to make vision and language models more grounded. In Proceedings of the IEEE International Conference on Computer Vision, pages 2591–2600, 2019. 1, 2, 3, 6, 14
[46] Jialin Wu and Raymond Mooney. Self-critical reasoning for robust visual question answering. In Advances in Neural Information Processing Systems, pages 8604–8614, 2019. 1, 2, 3, 6
[22] Chenchen Jing, Yuwei Wu, Xiaoxun Zhang, Yunde Jia, and Qi Wu. Overcoming language priors in vqa via decomposed linguistic representations. In AAAI, pages 11181–11188, 2020. 1, 2, 6
3、基于反事实的方法?CVPR2021? CSS?
[33] Yulei Niu, Kaihua Tang, Hanwang Zhang, Zhiwu Lu, Xian-Sheng Hua, and Ji-Rong Wen. Counterfactual vqa: A cause-effect look at language bias. arXiv preprint arXiv:2006.04315, 2020. 2, 6, 7
[8] Long Chen, Xin Yan, Jun Xiao, Hanwang Zhang, Shiliang Pu, and Yueting Zhuang. Counterfactual samples synthesizing for robust visual question answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10800–10809, 2020. 1, 2, 3, 6, 7, 12, 14
基于ensemble的方法根据question-only上的分支对样本再次赋予权重(减小这部分样本的重视程度?);基于Grounding的方法更好的利用已经标注好的视觉信息;基于反事实样本(CSS)的方法进一步利用这两种方法之间的联系来提高性能。
即使这样,现有的方法仍未充分利用视觉和语言信息(可能这就是大佬吧?)。参考文献给出观点论证:
[44] Robik Shrestha, Kushal Kafle, and Christopher Kanan. A negative case analysis of visual grounding methods for VQA. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 8172–8181, Online, July 2020. Association for Computational Linguistics. 2, 3, 5
和参考文献44类似,作者进一步采用三种策略来分析bias。与此同时,作者提出存在两种类型的语言bias,也就是摘要中提及的:1、训练集和测试集分布的gap;2、特定QA对之间的语义联系,即“捷径”

一般来说,长尾分布(数据偏重于一侧)是增加shortcut的一个因素,但是本文在实验中发现实际上有两个语言Bias的方面存在。采用基于Grounding Supervision或者ensemble regulation的方法并未强迫模型关注于视觉信息,所以作者提出Greedy Gradient Ensemble (GGE),一种嵌入有bias模型但模型无关的de-bias框架。设计理念:充分利用过拟合的现象:数据的bias部分被bias特征贪心的过拟合,从而使得base模型能够去解决bias不能解决的问题样本。
实验部分采用了不同的GGE变体模型论证了方法的泛化能力,并进一步证实了数据集的分布bias和shortcut bias在VQA中是语言bias的两个方面。
本文的主要贡献:
1、分析了VQA任务中的语言bias,将其分解为distribution bias & shortcut bias
2、新的模型无关的框架GGE,能够键入bias模型
3、性能好
三、相关工作
3.1 Debias with dataset construction
本小节主要讲解一些数据集(VQA v2, VQA-CP)的构建,因为这是最直接的解决数据bias的方法了。
3.2 Debias with model design
大佬发言:收集新的大尺度数据比较费时费力,所以关键是要提升模型的鲁棒性。涉及的方法有:GVQA、LDP、GVQE,后两者利用问题中的不同信息来更好地对问题进行表示。但是这些模型需要 预定义的问题分析器,所以很难实现(不错的理由,)。
最近的参考文献44表示仍然没有找到一个好的方式来测试系统实际上是否真的进行了visually grounded,所以到目前最有效的de-bias方式还是ensemble-based:构建一个question-only 的分支来明确地建模语言bias。例如RUBi、LMH、PoE, CSS,MFE,LFE等,但其中一些方法只关注于单个模态的分类问题,另一些基于GCE的算法依赖于学习过程中的超参数,且在去除bias的过程中只能处理一对属性(?)。
四、Revisiting Language Bias in VQA
4.1 问题定义
4.2 Experimental Analysis for Language Bias
本小节采用三个控制实验来研究 语言bias
0、baseline model UpDn
1、grounding-based method HINT
2、ensemble-based method RUBi LMH
3、counterfactual-based method CSS
4.2.1 Inverse Grounding Annotation
为了分析visual-grounding的作用,在改变humman-annotated 区域的重要性得分的情况下,Hint和CSS-V方法和他们原始的模型性能差不多,这表明了精确度收益并不与相关视觉区域相关。尽管这些方法能够回答困难的问题,但是仍在基于语言bias做出的回答,称之为“inverse language bias” (好嘲讽)。
4.2.2 Vision-only Model
在这个实验中,测试基于ensemble branch的方法:RUBi和LMH,直接喂给图像特征到分类器,所以无QA捷径可走。实验结果:RUBi下降了一点,但是LMHvo仍然超出了UpDnvo一大截,原因在于LMH主要惩罚训练集中最频繁的答案,使得最后的分类更加平衡,这也就意味着LMH能够有效消除分布bias。
4.2.3 Inverse Supervision for Balanced Classifier
为了测试“inverse supervision bias”能否提高精度,采用CSS,设计了“inverse supervision”策略:对于每一次迭代,采用不同监督方式,对参数更新两次 :1、采用真实标签训练来获得预测的答案,此为训练了一次;2、从不含第一次排序最高的标签的集合中随机抽取作为第二次标签进行训练,即CSS的简化版本:逐步地惩罚第一轮训练中置信度最高的答案,因此能够根据这种“inverse distribution bias”构成一个更加平衡的分类。
根据上表, UpDn v o , i s \textrm {UpDn}_{vo,is} UpDnvo,is精度的提升揭示了分布bias的存在, RUBi i s \textrm {RUBi}_{is} RUBiis进一步暗示了分布bias和shortcut bias两者为互补关系。在使用外部标注的情况下, LMH i s \textrm {LMH}_{is} LMHis能比得上CSS,但在VQAv2数据集上的精度会极度退化。接下来是这几次的实验结论:
- 准确度高并不能保证系统是真的根据视觉标签(有可能是bias)而建立答案分类;GT监督或者question-only 归一化可能会促使模型利用 inverse 的语言bias,而不是视觉信息(莫名的一股嘲讽意味);
- 在VQA中,分布bias和捷径bias是语言bias中的两面,单个ensemble分支不能(同时)建模这两种类型的bias。
五、方法
GGE:逐步的消除分布bias和捷径bias,强制模型关注图像信息。
5.1 Greedy Gradient Ensemble
这一部分公式有点多,还是看原文好些。
设 ( X , Y ) \mathcal(X, Y) (X,Y)为训练集, X X X是观测空间, Y Y Y是答案空间,采用交叉熵(BCE)损失:
L ( P , Y ) = − ∑ i = 1 C y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) \mathcal{L}(P, Y)=-\sum_{i=1}^{C} y_{i} \log \left(p_{i}\right)+\left(1-y_{i}\right) \log \left(1-p_{i}\right) L(P,Y)=−i=1∑Cyilog(pi)+(1−yi)log(1−pi)
C C C 表示最终分类的数量, p i = σ ( z i ) \mathcal p_{i}=\sigma\left(z_{i}\right) pi=σ(zi),其中 z i \mathcal z_{i} zi是类别 i \mathcal i i 的预测 logit \textrm {logit} logit, σ ( . ) \mathcal \sigma(.) σ(.)为sigmoid函数,模型通过最小化 f ( X ; θ ) \mathcal f(X;\theta) f(X;θ)和标签 Y Y Y的BCE损失来进行参数迭代:
min θ L ( σ ( f ( X ; θ ) ) , Y ) \min _{\theta} \mathcal{L}(\sigma(f(X ; \theta)), Y) θminL(σ(f(X;θ)),Y)
其中, f ( . ) f(.) f(.)为DNNs的超参数。
接下来根据上面的模型引出本文的方法:假设 B = { B 1 , B 2 , … , B M } B=\left\{B_{1}, B_{2}, \ldots, B_{M}\right\} B={B1,B2,…,BM}为其他先验模型提取出来的带有bias的特征,将bias模型和base模型的集合用标签 Y Y Y来表示:
min ϕ , θ L ( σ ( f ( X ; θ ) + ∑ i = 1 M h i ( B i ; ϕ i ) ) , Y ) \min _{\phi, \theta} \mathcal{L}\left(\sigma\left(f(X ; \theta)+\sum_{i=1}^{M} h_{i}\left(B_{i} ; \phi_{i}\right)\right), Y\right) ϕ,θminL(σ(f(X;θ)+i=1∑Mhi(Bi;ϕi)),Y)
其中 h i ( . ) h_{i}(.) hi(.) 为bias模型。
针对这个存在bias的模型,作者提出GGE:让 h i ( . ) h_{i}(.) hi(.)学习bias部分的数据,使得base模型能够学习无bias的数据分布,即 利用贪心算法使得bias模型提前过拟合数据。
那么如何操作呢?设当前函数空间内有 H m = ∑ i = 1 m h i ( B i ) \mathcal H_{m}=\sum\nolimits_{i=1}^{m}h_{i}(B_{i}) Hm=∑i=1mhi(Bi),找到一个 h m + 1 ( B m + 1 ) h_{m+1}(B_{m+1}) hm+1(Bm+1),使得 L ( σ ( H m + h m + 1 ( B m + 1 ) ) , Y ) \mathcal{L}\left(\sigma\left(\mathcal{H}_{m}+h_{m+1}\left(B_{m+1}\right)\right), Y\right) L(σ(Hm+hm+1(Bm+1)),Y) 减小(意味着bias减小)。如何减小?从理论上来说, h m + 1 h_{m+1} hm+1 可以是 L L L 在 H m \mathcal H_{m} Hm 上的负梯度,即有
− ∇ L ( H m , i ) : = ∂ L ( σ ( H m ) , Y ) ∂ H m , i = 2 y m , i σ ( − 2 y m , i H m , i ) -\nabla \mathcal{L}\left(\mathcal{H}_{m, i}\right):=\frac{\partial \mathcal{L}\left(\sigma\left(\mathcal{H}_{m}\right), Y\right)}{\partial \mathcal{H}_{m, i}}=2 y_{m, i} \sigma\left(-2 y_{m, i} \mathcal{H}_{m, i}\right) −∇L(Hm,i):=∂Hm,i∂L(σ(Hm),Y)=2ym,iσ(−2ym,iHm,i)
于是对于分类任务来说,类别 i i i 的概率为 i : σ ( f i ( x ) ) ∈ { 0 , 1 } i:\sigma\left(f_{i}(x)\right){\in}{\lbrace{0,1}\rbrace} i:σ(fi(x))∈{0,1}。又由于是 0 − 1 0-1 0−1 分布,所以直接将负梯度作为伪标签,采用BCE损失来优化 h m + 1 ( B m + 1 ) h_{m+1}(B_{m+1}) hm+1(Bm+1)(脑洞确实大啊):
L m + 1 = L ( σ ( h m + 1 ( B m + 1 ; ϕ m + 1 ) ) , − ∇ L ( H m ) ) L_{m+1}={\mathcal L}({\sigma}(h_{m+1}(B_{m+1};{\phi}_{m+1})),-{\nabla}{\mathcal L({\mathcal H_{m}}))} Lm+1=L(σ(hm+1(Bm+1;ϕm+1)),−∇L(Hm))
在整合完所有的bias模型后,对base模型进行优化:
L b ( θ ) = L ( σ ( f ( X ; θ ) ) , − ∇ L ( H M ) ) . L_{b}(\theta)=\mathcal{L}\left(\sigma(f(X ; \theta)),-\nabla \mathcal{L}\left(\mathcal{H}_{M}\right)\right) . Lb(θ)=L(σ(f(X;θ)),−∇L(HM)).
注意:此处的损失函数要考虑正负样本的选择。为了使得上面的优化方法适用于 SGD \textrm {SGD} SGD,另外再设计了两种优化策略, GGE-interation, GGE-togethe \text {GGE-interation, GGE-togethe} GGE-interation, GGE-togethe。而base模型最终的优化方法为:
L ( Θ ) = L b ( θ ) + ∑ m = 1 M L m ( ϕ m ) L(\Theta)=L_{b}(\theta)+\sum_{m=1}^{M} L_{m}\left(\phi_{m}\right) L(Θ)=Lb(θ)+m=1∑MLm(ϕm)
PS:以上是作者的算法部分,吐槽一下千万别整这么多符号,也没介绍好哪个是哪个,迷惑,还是看接下来咋实现的吧。
5.2 GGE Implementation for Robust VQA
这一小节是对本文定义的两个语言bias(distribution & shortcut)进行分析。
5.2.1 Distribution Bias
分布bias: 基于问题类型的答案分布bias。由于问题类型的信息是从可以从问题中直接得到,所以也就和语言bias无关(有关的有两个1、长尾,2、捷径)。用公式表现为:
B d i = p ( a i ∣ ( t i ) ) B_{d}^{i}=p(a_{i}|(t_{i})) Bdi=p(ai∣(ti))
其中, t i t_{i} ti表示问题 q i q_{i} qi的类型。
5.2.2 Shortcut Bias
捷径bias:特定QA对之间的语义关联。可以用仅含有问题的分支来表示,用公式表示:
B q i = c q ( e q ( q i ) ) B_{q}^{i}=c_{q}(e_{q}(q_{i})) Bqi=cq(eq(qi))
其中, c q c_{q} cq表示为问题映射到向量,即 Q → R C Q{\rightarrow}{\mathbb R}^{C} Q→RC
接下来就是为了验证分布bias和捷径bias是两种互补性bias,设计了三个版本的 GGE \text {GGE} GGE来针对不同语言bias中的ensemble。
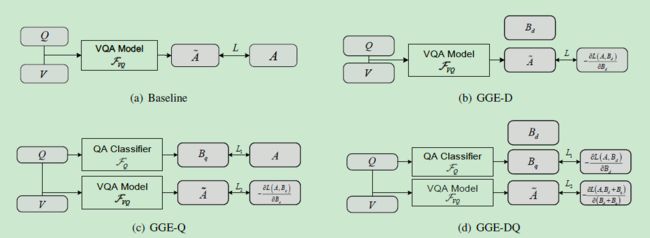
5.2.3 GGE-D
如上图b所示, GGE-D \text {GGE-D} GGE-D版本仅有模型的分布bias参与ensemble,base模型的损失为:
L = L ( σ ( A ~ ) , − ∇ ( B d , A ) ) L={\mathcal L}({\sigma}(\tilde{A}),-{\nabla}(B_{d},A)) L=L(σ(A~),−∇(Bd,A))
其中, A ~ \tilde{A} A~为预测的答案, A A A为标签答案, B d B_{d} Bd为预测的分布bias。
5.2.4 GGE-Q
如上图c所示,使用仅包含问题的分支来针对捷径bias,采用标签答案来优化该问题分支:
L 1 = L ( σ ( B q ) , − ∇ L ( B d , A ) ) L_{1}={\mathcal L}({\sigma}(B_{q}),-{\nabla}{\mathcal L}(B_{d},A)) L1=L(σ(Bq),−∇L(Bd,A))
相应的base模型损失为:
L 2 = L ( σ ( A ~ ) , − ∇ L ( σ ( B q ) , A ) ) L_{2}={\mathcal L}({\sigma}({\tilde A}),-{\nabla}{\mathcal L}({\sigma}(B_{q}),A)) L2=L(σ(A~),−∇L(σ(Bq),A))
5.2.5 GGE-DQ
如上图d所示,针对两种bias(分布bias & 捷径bias)同时进行操作。
其中,问题bias的损失函数为:
L 1 = L ( σ ( B q ) , − ∇ L ( B d , A ) ) L_{1}={\mathcal L}({\sigma}(B_{q}),-{\nabla}{\mathcal L}(B_{d},A)) L1=L(σ(Bq),−∇L(Bd,A))
base模型的损失为:
L 2 = L ( σ ( A ~ ) , − ∇ L ( σ ( B q ) + B d , A ) ) L_{2}={\mathcal L}({\sigma}({\tilde A}),-{\nabla}{\mathcal L}({\sigma}(B_{q})+B_{d},A)) L2=L(σ(A~),−∇L(σ(Bq)+Bd,A))
针对这些损失,采用补充材料中的 GGE-iter or GGE-tog \text {GGE-iter or GGE-tog} GGE-iter or GGE-tog来对 L 1 & L 2 L_{1} \& L_{2} L1&L2进行迭代。
5.3 Connection to Boosting
Boosting定义:通过联合多种弱分类器(bias高,变化少)来产生强分类器(bias低,变化少)。要求则是每一个学习器都必须足够弱,否则就很容易过拟合。但由于神经网络的拟合能力贼强,所以很难利用深度模型来满足符合要求的低bias,低变化的分类器。因此,本文提出利用神经网络的过拟合现象,根据bias的弱特征来过拟合bias分布。在测试阶段,仅采用经bias梯度下降后的base模型来进行测试。
从另一方面来说,本文的思想接近于梯度增强(Gradient Boost),但是梯度增强必须贪婪地反复进行弱学习。对于神经网络来说,通过反向传播比较复杂,所以采用 GGE-iteration & GGE-together \text {GGE-iteration \& GGE-together} GGE-iteration & GGE-together策略沿着批量梯度下降的方向来更新参数。
六、实验
实验数据集: VQA-CP v2 & VQA v2 \text {VQA-CP v2 \& VQA v2} VQA-CP v2 & VQA v2
6.1 评估指标
作者认为:精度高并不足矣暗示模型的视觉建模能力,所以出现了参考文献44中的新的指标: CPIG \text{CPIG} CPIG
[44] Robik Shrestha, Kushal Kafle, and Christopher Kanan. A negative case analysis of visual grounding methods for VQA. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 8172–8181, Online, July 2020. Association for Computational Linguistics. 2, 3, 5
CPIG \text{CPIG} CPIG:衡量正确推理的能力指标,具体来说是正确的Instance在答案对应的图像最敏感的top-N个部分。例如 1 − C P I G {1-CPIG} 1−CPIG将其定义为 C G R (Correct Grounding for Right prediction) {CGR}\text{(Correct Grounding for Right prediction)} CGR(Correct Grounding for Right prediction),用公式表示为:
% C G R = N r g , r p N r p × 100 % {\%}CGR= {\frac{N_{rg,rp}}{N_{rp}}}{\times}100\% %CGR=NrpNrg,rp×100%
其中, N r p N_{rp} Nrp为正确预测的数量, N r g , r p N_{rg,rp} Nrg,rp为不正确的答案对应不正确区域的数量。
但是作者认为这种办法区分度不高,虽然模型具有高的 CGR \text{CGR} CGR,但是实际上没有足够的视觉信息用于分类。So,如果模型定位到正确的目标但是却没有正确的答案,那么很有可能就是利用了语言bias而不是图像的预测信息。因此为了衡量模型是否真的使用到了视觉信息来预测答案,引入了新的评判指标, CGW \text{CGW} CGW:具有正确的视觉区域但却回答错误的数量/错误预测数量的百分比,用公式表示为:
% C G W = N r g , w p N w p × 100 % {\%}CGW={}{\frac{N_{rg,wp}}{N_{wp}}}{\times}100{\%} %CGW=NwpNrg,wp×100%
其中, N w p N_{wp} Nwp为预测错误的数量, N r g , w p N_{rg,wp} Nrg,wp为模型提供正确的图像区域但却回答错误的数量。
为了清楚的进行比较两种指标,作者对这两个指标做减法,得出 CGD(Correct Grounding Difference) \text{CGD(Correct Grounding Difference)} CGD(Correct Grounding Difference):
% C G D = % C G R − % C G W {\%}CGD={\%}CGR-{\%}CGW %CGD=%CGR−%CGW
CGD \text{CGD} CGD衡量了模型是否真的依赖图像的视觉区域来预测答案,该指标与 Accuracy \text{Accuracy} Accuracy同等重要。采用 CGD \text{CGD} CGD指标后, UpDn, HINinv and CSS-Vinv \text{UpDn, HINinv and CSS-Vinv } UpDn, HINinv and CSS-Vinv 的结果表明这些方法并非利用视觉信息来做出答案预测。
6.2 Comparison with State-of-the-art Methods
用来进行对比的模型: HINT,SCR,AdvReg,RUBi,LMH,MFE,GVQE,DLP,CF-VQA,CSS \text{HINT,SCR,AdvReg,RUBi,LMH,MFE,GVQE,DLP,CF-VQA,CSS} HINT,SCR,AdvReg,RUBi,LMH,MFE,GVQE,DLP,CF-VQA,CSS,具体请查看原文参考文献,这里就不粘贴了。
实验结果表明 GGE-DQ \text{GGE-DQ} GGE-DQ效果最佳。有个现象要注意一下,一些采用entropy 归一化dorp方法的模型几乎在VQAv2上的性能下降了10%,可能是过度纠正bias,从而使得可能依赖于反语言Bias(好讽)。
6.3 Ablation Studies

第一组消融实验:贪心算法能否保证bias模型学到bias数据;
比较对象: SUM-DQ & LMH-RUBi \text{SUM-DQ {\&} LMH-RUBi} SUM-DQ & LMH-RUBi;

第二组消融实验:比较分布bias和捷径bias,实验结果表明这两种bias是两种语言bias。
6.4 Generalization of GGE
6.4.1 Self-Ensemble
将 GGE \text{GGE} GGE嵌入到其他模型上,看看效果;

6.4.2 Generalization for Loss Function
对比不同的损失函数,表4含有实验结果。
6.4.3 Generalization for Base Model
由于 GGE \text{GGE} GGE是模型无关的,额外测试了两种模型 BAN & S-MRL \text{BAN {\&} S-MRL} BAN & S-MRL 作为base模型。
6.5 Qualitative Evaluation
七、 结论
语言bias可以分解为分布bias和捷径bias,减少这俩bias的方法: GGE \text{GGE} GGE
八、补充材料
这一部分我打算和源码一起看着撸一遍,很多算法原理啥的,也算是给自己挖个坑吧~
写在最后
这篇文章没有在模型上多下功夫,而是注重损失函数,说明这一块也是重点huo,建议配合源码熟悉,因为怎么设计的具体性的实施细节,论文并未提及,相信源码会给我们提供一点经验。另外,本文应该是受到参考文献44的启发,顺藤摸瓜看一下应该收获会更大。
(Ps:终于马马虎虎的写完了,这篇文章公式挺多的,刚好锻炼我用 latex敲公式的技能,Haha~)


