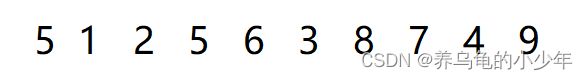数据结构-排序
本节目标:
1.排序的概念及其运用
2.常见排序算法的实现
3.排序算法复杂度及稳定性分析
1.排序的概念及其应用
1.1排序的概念
排序就是按照某个我们设定的关键字,或者关键词,递增或者递减,完成这样的操作就是排序。
1.2排序的应用
排序在日常生活中很常见的,想前几天刚出的软科高校排名,就用到了排序的思想,关键词就是软科,按照递增的顺序排列。如下图所示:
以及我们上淘宝的时候,也会用到排序的思想,我们想买个手机,筛选条件,按照个人选择不同给出的答案不同,用的人注重品牌,有的人注重价格,有的女孩更注重像素,如下图所示:
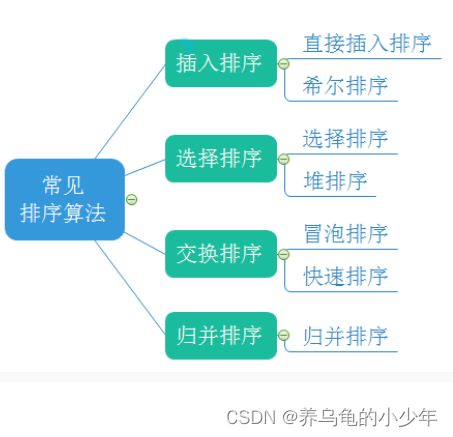
1.3常见的排序算法
2.常见的排序算法实现
2.1插入排序
2.1.1基本思想
其实插入排序的思想,几乎我们每个人都会,插入排序就像我们打的扑克,从未知的一副牌中,我们开始往手里揭牌,拿起第一张放在手中,再次拿起一张牌的时候,就要和手里的牌对比,如果比手里的牌大就往后排,如果比手里的牌小的话,就排在这张牌之前,以此类推。一副牌拿完之后,我们手里的牌也就按照递增的顺序排好了。
2.1.2直接插入排序:
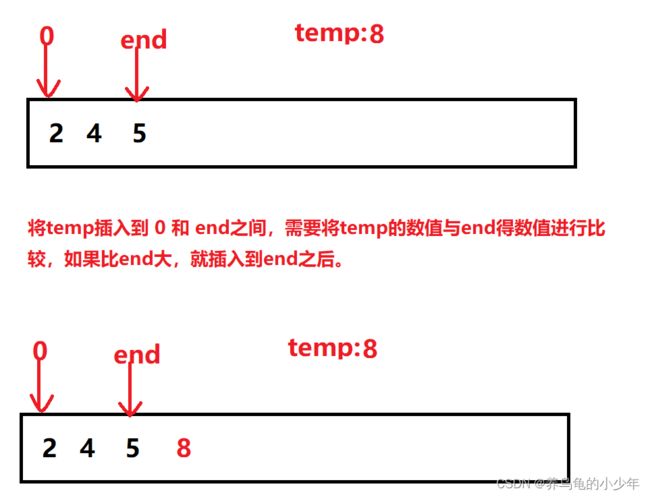
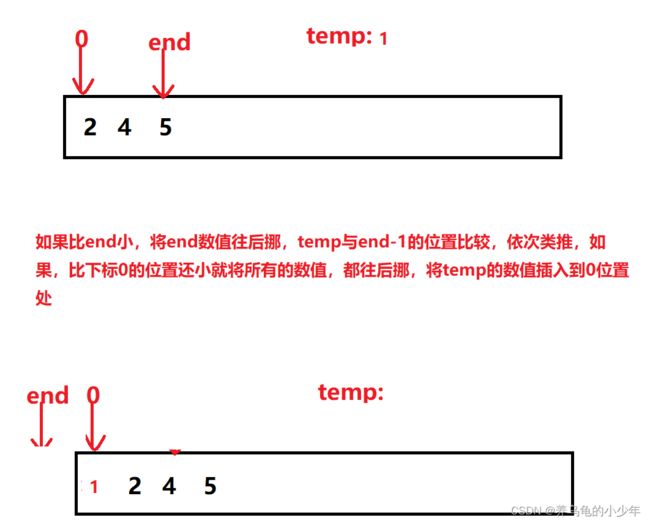
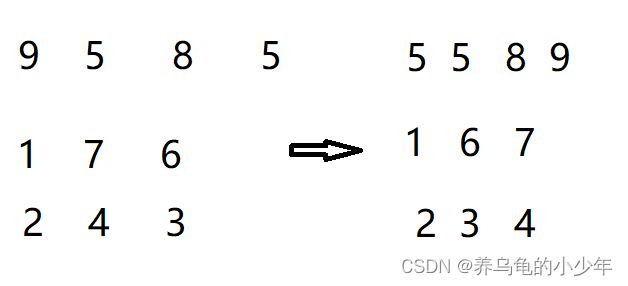
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。图解如下:
当插入的数比前一个数字还大时:
当插入的数字比数组中所有的数都要小的时候:
动态图解如下:
 插入排序
插入排序
代码实现:
void InsertSort(int* a, int n)
{
//遍历数组中所有元素
for (int i = 1; i < n; i++)
{
//单趟排序
int end = i - 1;
int temp = a[i];//temp存储的是元素数值
while (end >= 0)//一直比较到 数组第一个元素完成
{
if (temp < a[end])
{
a[end + 1] = a[end];
--end;
}
else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小
{
break;
}
}
a[end + 1] = temp;
}
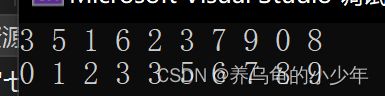
}结果对比:
在主程序中,我们调用插入排序函数,并查看最终是否实现 有序排序。
void TestInsertSort()
{
int a[] = { 3,5,1,6,2,3,7,9,0,8 };
PrintArray(a, sizeof(a) / sizeof(int));
InsertSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
TestInsertSort();
return 0;
}分析总结:
直接插入排序时间复杂度:最坏情况下,逆序有序,每个元素都要一个个比较,最终形成等差数列, 1 +2 +3 + ........N 时间复杂度为 O(N^2) ;最好的情况下,有序,1 + 1 + 1 + .......1时间复杂度为O(N) 总结来看 对于插入排序,元素集合越接近有序,算法时间效率越高。
2.1.3希尔排序(缩小增量排序):
希尔排序也是插入排序的一种,它又称缩小增量排序法,他其实是在插入排序上的一种优化,通过上面的分析,我们知道插入排序时间复杂度最好的情况,也就是接近有序的时候,他的时间复杂度为 O(N),最坏的情况下 无序的时候 为 O(N^2)。如果我们能先让数组接近有序之后,在对他进行排序,会大大减小算法时间复杂度。所以希尔大佬就研究出了希尔排序。
它的实现主要通过两步骤,第一步:预排序,让数组接近有序,第二步:插入排序。
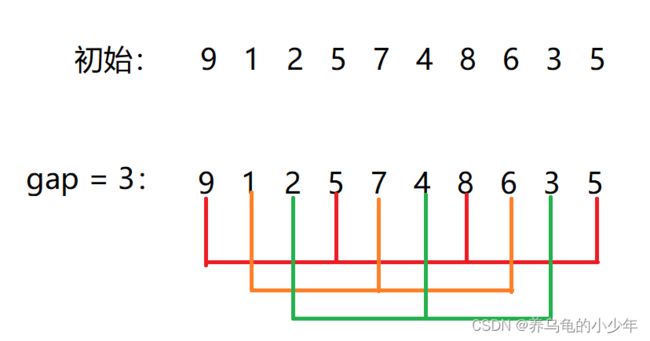
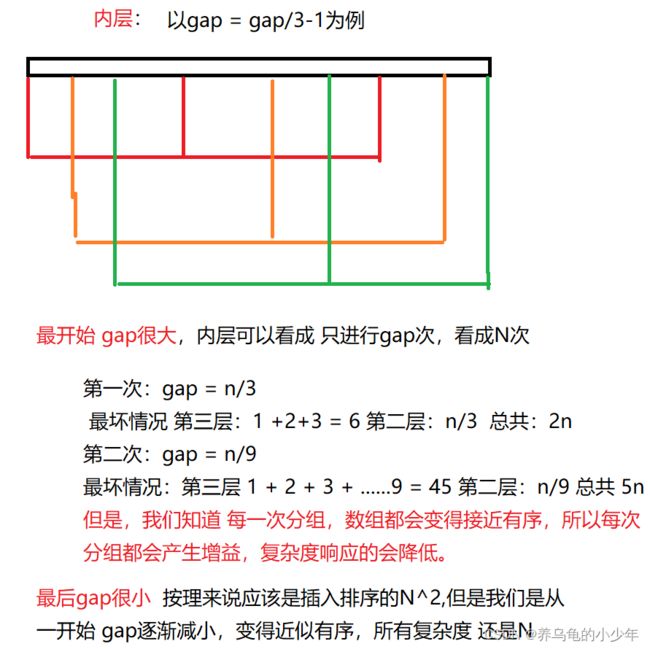
分组预排:
将无序的数组,按照间隙gap进行分组,将数组分成n/gap组,然后分组进行插入排序,因为有了gap所以时间复杂度会减小,如下图所示:
分组直接插入排序:
gap为3排序实现结果:
当gap依次减小,数组慢慢接近有序,最后gap为1时候,数组已经近似有序,再插入排序依次,数组就会实现有序的同时,算法时间复杂度最低。
代码实现:
void ShellSort(int* a, int n)
{
int gap = 3;
for (int j = 0; j < gap; j++)
{
for (int i = j; i = 0)//一直比较到 数组第一个元素完成
{
if (temp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小
{
break;
}
}
a[end + gap] = temp;
}
}
} 改进一下:
void ShellSort(int* a, int n)
{
int gap = 3;
for (int i = 0; i = 0)//一直比较到 数组第一个元素完成
{
if (temp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小
{
break;
}
}
a[end + gap] = temp;
}
} 我们发现gap越大虽然,跑的很快但是不接近有序,gap越小跑的慢,但是接近有序,所以需要设计合适的gap,减少复杂度的同时,保证最后一次排序 gap为1,通常 我们设计的gap,为n / 2,或者 n/3 - 1。
具体代码如下:
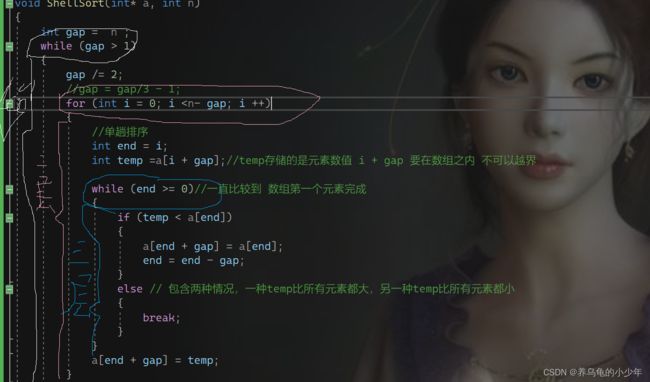
void ShellSort(int* a, int n)
{
int gap = n ;
while (gap > 1)
{
gap /= 2;
//gap = gap/3 - 1;
for (int i = 0; i = 0)//一直比较到 数组第一个元素完成
{
if (temp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小
{
break;
}
}
a[end + gap] = temp;
}
}
} 结果:
分析总结:
希尔排序的时间复杂度分析:
对于外层:是我们熟悉的二分或者三分 复杂度 最后为logN
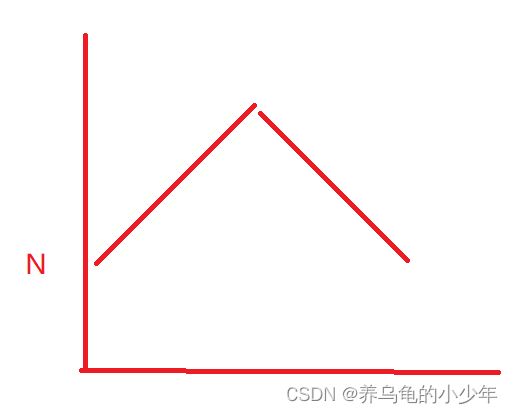
对于内部两层,当gap很大时候,可以看成N,当gap很小时,经过多次预排序,接近有序 复杂度也是N,我们在以gap/3分析中间的变化:图解分析如下:
所以 我们可以说 希尔排序时间复杂度近似 N*logN 但是每次预排都会有增益,他分组之后复杂度应该近似下图:
所以,虽然希尔的时间复杂度近似在N*logN这个等级,但是要比其大一点,查阅相关资料,对于希尔时间复杂度,通常是这么说的
2.2选择排序
2.2.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.2.2直接选择排序
在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
直接选择排序单趟寻找到最大的或最小的,实现升序的话就与最左边的交换,降序就与最右边交换,我们可以用代码实现左右共同查找的方式。如下所示:
void SelectSort(int* a, int n)
{
//初试状态
int left = 0;
int right = n - 1;
while (left < right)
{
//取最小值,最大值下标为最左边的 位置
int min = left, max = left;
for (int i = left + 1; i < right; i++)
{
if (a[i] < a[min])
{
min = i;
}
else if (a[i] > a[max])
{
max = i;
}
}
swap(&a[left], &a[min]);
if (left == max) //防止出现 left位置上放的是最大值
{
max = min;
}
swap(&a[right], &a[max]);
left++;
right--;
}
}结果分析:
选择排序的时间复杂度,还是比较low的不管怎么选,都是O(N^2) 。
2.2.3堆排序
堆排序是我们的老朋友了,堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
代码如下:
//向下调整
void AjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1; //孩子和父亲的关系
while (child < n) // 遍历条件
{
if (child + 1 < n && a[child + 1] > a[child]) //左右孩子 选择最大的那个,同时兼顾 右孩子也要小于边界
{
++child;
}
if (a[child] > a[parent]) // 建大堆
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--) // 从最后一个节点的父亲 开始向下调整 保证父亲比孩子大
{
AjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&a[end], &a[0]); // 交换 根节点 和最后一个位置的数值
AjustDown(a, end, 0);
--end;
}
}总结:
堆排的时间复杂度 ,我们在堆排序那个章节推过,这里我直接说结论:o(N * logN)。