用python将时间序列信号或一维数组 转化成 图像的几种方法

用python将时间序列信号或一维数组转化成图像的几种方法

深度学习在计算机视觉有了非常广泛的应用，视觉图像数据为二维数据，而在故障诊断领域的数据，来自于传感器的采集，属于典型的一维时间序列，因而绝大多数问题可以抽象成时间序列分类(TSC)问题。若将时间序列或一维数组转化为图像，再应用深度学习的模型做分析，是一种很不错的方法，且这种方法在很多论文中已有实践。

---

---

一、利用PIL库

话不多说上代码。

import numpy as np
from PIL import Image
'''
读取时间序列的数据
怎么读取需要你自己写
'''
#把数据转成array形式
TSC = np.array(TSC)
#将长为L的时间序列转成m*n的矩阵， L = m*n
result = idx.reshape((m, n))
#矩阵归一化,调用Image
result = (result - np.min(result)) / (np.max(result) - np.min(result))
im = Image.fromarray(result*255.0)
im.convert('L').save("1.jpg",format = 'jpeg')

这是我得到的128*256大小的灰度图

---

二、利用CV库

看这篇博客，这个方法和利用PIL库有异曲同工之处

python-OpenCV 将数组转换成灰度图和彩图

---

二、利用pyts库

pyts专用于时间序列分类的Python软件包。它旨在通过提供预处理和实用工具以及几种时间序列分类算法的实现，使时间序列分类易于访问。
在这个库中可将时间序列数据转化成：
Recurrence Plot （递归图）
Markov Transition Field （马尔可夫变迁场）
Gramian Angular Field （格拉米角场）
参考论文：

《Imaging Time Series to Improve Classification and Imputation》
《Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks》
《Encoding Temporal Markov Dynamics in Graph for Time Series Visualization》

1.Recurrence Plot （递归图）

递柜图是从时间序列获得的图像，表示每个时间点之间的距离。可以使用阈值对图像进行二值化。
一般递归图(recurrence plot, RP)是分析时间序列周期性、混沌性以及非平稳性的一个重要方法，可以揭示时间序列的内部结构，给出有关相似性、信息量和预测性的先验知识。递归图特别适合短时间序列数据，可以检验时间序列的平稳性、内在相似性。
最初由Eckmann等人于1987年提出，主要用于对非线性动力系统的定性分析。递归图已经成功的应用在诸如气候变化，脑心电图分析，股市分析等众多领域。
实现代码：

import matplotlib.pyplot as plt
from pyts.image import RecurrencePlot
'''
读取时间序列的数据
怎么读取需要你自己写
X为ndarray类型数据
'''
# Recurrence plot transformation
rp = RecurrencePlot(threshold='point', percentage=20)
X_rp = rp.fit_transform(X)

# Show the results for the first time series
plt.figure(figsize=(5, 5))
plt.imshow(X_rp[0], cmap='binary', origin='lower')
plt.title('Recurrence Plot', fontsize=16)
plt.tight_layout()
plt.show()

长度为1766的振动信号时间序列得到的递归

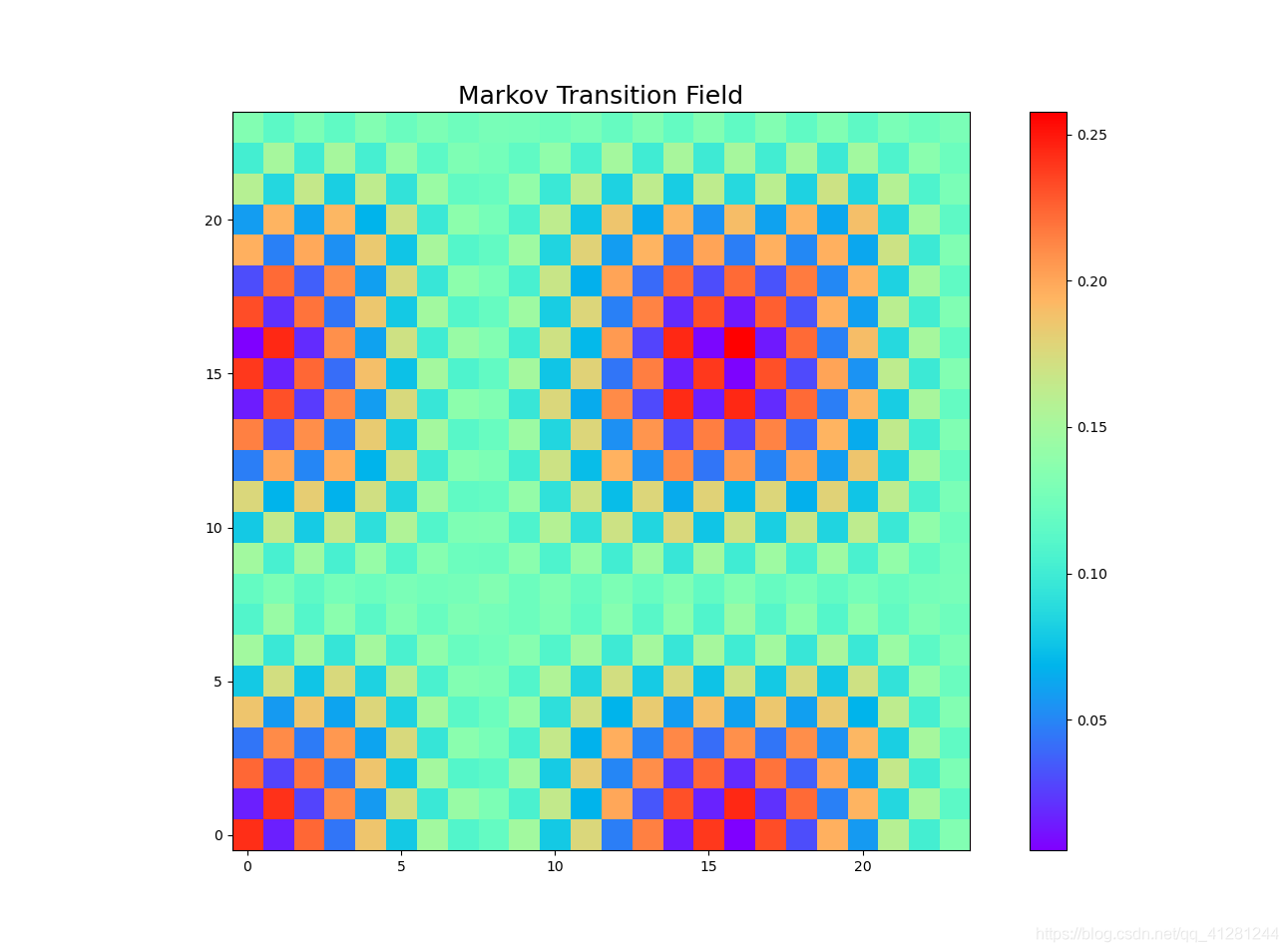
2.Markov Transition Field （马尔可夫变迁场）

马尔可夫转变场是从时间序列获得的图像，表示离散时间序列的转变概率场。可以使用不同的策略对时间序列进行分类。

import matplotlib.pyplot as plt
from pyts.image import MarkovTransitionField
'''
读取时间序列的数据
怎么读取需要你自己写
X为ndarray类型数据
'''
# MTF transformation
mtf = MarkovTransitionField(image_size=24)
X_mtf = mtf.fit_transform(X)

# Show the image for the first time series
plt.figure(figsize=(5, 5))
plt.imshow(X_mtf[0], cmap='rainbow', origin='lower')
plt.title('Markov Transition Field', fontsize=18)
plt.colorbar(fraction=0.0457, pad=0.04)
plt.tight_layout()
plt.show()

长度为1766的振动信号时间序列得到的马尔可夫变迁场

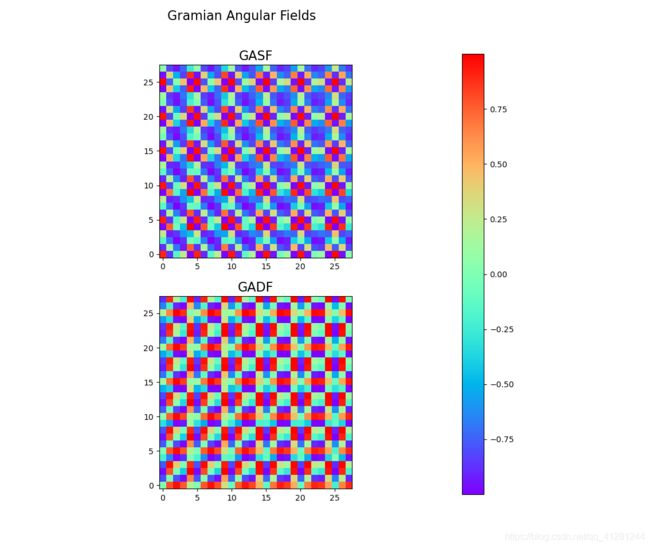
3. Gramian Angular Field （格拉米角场）

Gramian Angular Field （格拉米角场）的原理可以看这篇博客：

Python：使用 pyts 把一维时间序列转换成二维图片

实现代码：

# Author: Johann Faouzi 
# License: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.axes_grid1 import ImageGrid, make_axes_locatable
from pyts.image import  GramianAngularField
'''
读取时间序列的数据
怎么读取需要你自己写
X为ndarray类型数据
'''
# Transform the time series into Gramian Angular Fields
gasf = GramianAngularField(image_size=28, method='summation')
X_gasf = gasf.fit_transform(X)
gadf = GramianAngularField(image_size=28, method='difference')
X_gadf = gadf.fit_transform(X)

# Show the results for the first time series
axs = plt.subplots()
plt.subplot(211)
plt.imshow(X_gasf[0], cmap='rainbow', origin='lower')
plt.title("GASF", fontsize=16)
plt.subplot(212)
plt.imshow(X_gadf[0], cmap='rainbow', origin='lower')
plt.title("GADF", fontsize=16)

#plt.axes((left, bottom, width, height)
cax = plt.axes([0.7, 0.1, 0.02, 0.8])
plt.colorbar(cax = cax)
plt.suptitle('Gramian Angular Fields', y=0.98, fontsize=16)
plt.tight_layout()
plt.show()

长度为1766的振动信号时间序列得到的格拉米角场