【youcans的深度学习 D01】PyTorch例程:从极简线性模型开始
欢迎关注『youcans的深度学习』系列
【youcans的深度学习 D01】PyTorch 例程:从极简线性模型开始
-
- 1. PyTorch 建模的基本步骤
- 2. 线性模型的结构
- 3. 建立 PyTorch 线性模型
-
- 3.1 准备数据集
- 3.2 定义线性模型类
- 3.3 建立一个线性模型
- 3.4 模型训练
- 3.5 模型推断
- 4. PyTorch 线性模型例程
- 5. 小结
在前面的章节我们已经介绍了 Pytorch 中的数据加载和模型建立。
本节在此基础上,实现一个最简单的案例:创建一个线性网络模型。该模型虽然极简,但已经完整包括了 PyTorch 建立模型、模型训练和模型预测的关键步骤,有助于读者理解 PyTorch 深度学习的基本方法。
1. PyTorch 建模的基本步骤
使用 PyTorch 建立、训练和使用神经网络模型的基本步骤如下。
- 准备数据集(Prepare dataset)。
- 创建网络模型(Design model using Class)。
- 定义损失函数和优化器(Construct loss and optimizer)。
- 模型训练(Trainning the model)。
- 模型测试(Testing the model)。
- 模型保存与加载(Saving and loading a model)。
- 模型推理(Inferring model)。
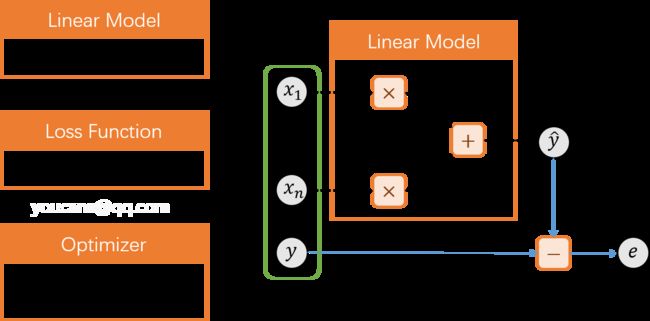
2. 线性模型的结构
对于线性模型
y = w i ∗ x i + b , i = 1 , . . . n y = w_i * x_i + b, \space i=1,...n y=wi∗xi+b, i=1,...n
3. 建立 PyTorch 线性模型
3.1 准备数据集
简单地,考虑 n=1 时的单输入单输出系统:
y = w ∗ x + b y = w * x + b y=w∗x+b
随机生成一组样本输入值,试验得到对应的样本输出值,构造训练样本数据集 {Xtrain, Ytrain}。
PyTorch 中的基本数据结构是张量 Tensor,训练样本数据集的输入 Xtrain 和输出 Ytrain 的类型都是 Tensor。
# (1) 建立样本数据集
Ntrain = 100 # 训练样本数目
Xtrain = torch.rand(Ntrain, 1) # 输入值,均匀分布
noise = torch.normal(0.0, 0.1, Xtrain.shape) # 高斯分布,加性噪音
Ytrain = 3.6 + 2.5 * Xtrain + noise # 模拟试验的输出值
print("Xtrain.shape: {}, Ytrain.shape: {}".format(Xtrain.shape, Ytrain.shape))
3.2 定义线性模型类
使用 PyTorch 构造神经网络模型,需要运用__call__()和__init__()方法定义模型类 Class。__init__()方法是类的初始化函数,类似于C++的构造函数。__call__()方法使类对象具有类似函数的功能。
# (2) 定义线性模型类
class LinearModel(torch.nn.Module):
def __init__(self): # 构造函数
super(LinearModel, self).__init__()
# 构造 linear 对象,并说明输入输出的维数,第三个参数默认为 true
self.linear = torch.nn.Linear(1, 1) # 包括 2 个参数 weight 和 bias
def forward(self, x): # 重写 forward 函数
y_pred = self.linear(x) # 可调用对象,计算 y=wx+b
return y_pred
nn.Module 是所有神经网络单元(neural network modules)的基类。PyTorch在nn.Module中实现了__call__()方法,在 __call__() 方法中调用 forward 函数。
nn.Linear 定义一个神经网络的线性层 ,方法如下:
torch.nn.Linear(in_features, # 输入的神经元个数
out_features, # 输出神经元个数
bias=True # 是否包含偏置
)
表示对输入 X n ∗ i X_{n*i} Xn∗i 进行线性加权求和:
Y n ∗ o = X n ∗ i W i ∗ o + b Y_{n*o} = X_{n*i} W{i*o} + b Yn∗o=Xn∗iWi∗o+b
本例中输入 x 和输出 y 都是一维,nn.Linear(1, 1) 中的参数 (1, 1) 表示 i=o=1 。
3.3 建立一个线性模型
建立线性模型,包括三个步骤:
- 实例化线性模型对象
- 设置损失函数 Loss
- 设置优化器 optim
# (3) 实例化线性模型对象
model = LinearModel() # 实例化 LinearModel
# (4) 构造损失函数 Loss
criterion = torch.nn.MSELoss(reduction='sum')
# (5) 构造优化器 optim
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # lr为学习率
# 优化器对象创建时需要传入模型参数 model.parameters(),将扫描 module中的所有成员
torch.nn.functional 模块包含内置损失函数,均方误差损失为 mse_loss。
torch.optim.SGD 表示随机梯度下降优化器,注意要将 model 的参数 model.parameters() 传给优化器对象,以便 SGD 优化器扫描需要优化的参数。
3.4 模型训练
模型训练的基本步骤是:
- 前馈计算模型的输出值;
- 计算损失函数值;
- 计算权重 weight 和偏差 bias 的梯度;
- 根据梯度值调整模型参数;
- 将梯度重置为 0(用于下一循环)。
# (6) 模型训练
epoch_list = []
loss_list = []
for epoch in range(100):
Ypred = model(Xtrain) # 前馈计算模型输出值
loss = criterion(Ypred, Ytrain) # 计算损失函数
optimizer.zero_grad() # 梯度归零
loss.backward() # 误差反向传播
optimizer.step() # 权重更新
epoch_list.append(epoch) # 记录迭代次数
loss_list.append(loss.item()) # 记录损失函数
if epoch%10==0:
print("Epoch {}: loss={:.4f}".format(epoch, loss.item()))
3.5 模型推断
# (7) 模型预测
Ypred = model(Xtrain)
4. PyTorch 线性模型例程
# DNNdemo01_v1.py
# DNNdemo of PyTroch: Linear regression
# PyTorch 例程: 01 线性回归
# Copyright: [email protected]
# Crated: Huang Shan, 2023/03/11
import torch
import matplotlib.pyplot as plt
# (2) 定义线性模型类
class LinearModel(torch.nn.Module):
def __init__(self): # 构造函数
super(LinearModel, self).__init__()
# 构造 linear 对象,并说明输入输出的维数,第三个参数默认为 true
self.linear = torch.nn.Linear(1, 1) # 包括 2 个参数 weight 和 bias
def forward(self, x): # 重写 forward 函数
ypred = self.linear(x) # 可调用对象,计算 y=wx+b
return ypred
if __name__ == "__main__":
# (1) 建立样本数据集
Ntrain = 50 # 训练样本数目
Xtrain = torch.rand(Ntrain, 1) # 输入值,均匀分布
noise = torch.normal(0.0, 0.1, Xtrain.shape) # 高斯分布,加性噪音
Ytrain = 2.0 * Xtrain + 3.6 + noise # 模拟试验的输出值
print("Xtrain.shape: {}, Ytrain.shape: {}".format(Xtrain.shape, Ytrain.shape))
# (3) 实例化线性模型对象
model = LinearModel() # 实例化 LinearModel
# (4) 设置损失函数 Loss 和 优化器 optim
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # lr为学习率
# 优化器对象创建时需要传入模型参数 model.parameters(),将扫描 module中的所有成员
# (5) 模型训练
epoch_list = []
loss_list = []
for epoch in range(10): # 训练轮次
Ypred = model(Xtrain) # 前馈计算模型输出值
loss = criterion(Ypred, Ytrain) # 计算损失函数
optimizer.zero_grad() # 梯度归零
loss.backward() # 误差反向传播
optimizer.step() # 权重更新
epoch_list.append(epoch) # 记录迭代次数
loss_list.append(loss.item()) # 记录损失函数
if epoch%10==0:
print("Epoch {}: loss={:.4f}".format(epoch, loss.item()))
# 迭代训练后的模型参数 weight 和 bias
print("Linear Model: y = w * x + b")
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
# (6) 模型预测
Ypred = model(Xtrain)
print("Xtest.shape: {}, Ytest.shape: {}".format(Xtrain.shape, Ypred.shape))
# (7) 绘图
plt.figure(figsize=(9, 4))
plt.suptitle("Response curve of activation function")
plt.subplot(121)
plt.plot(Xtrain.numpy(), Ytrain.numpy(), 'ro', label="train")
plt.plot(Xtrain.numpy(), Ypred.detach().numpy(), 'bx', label="model")
plt.xlabel('x'), plt.ylabel('y'), plt.legend()
plt.title("Prediction of linear model")
plt.subplot(122)
plt.plot(epoch_list, loss_list)
plt.xlabel('times'), plt.ylabel('loss')
plt.title("Loss of Linear Model")
plt.show()
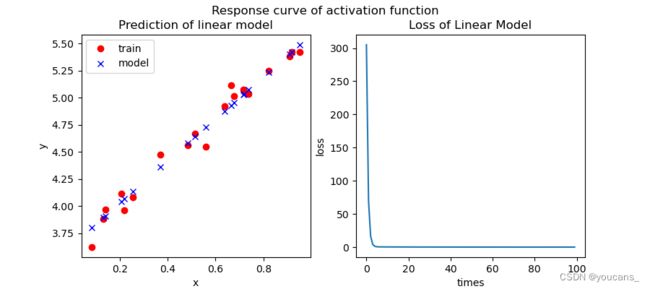
运行结果:
Xtrain.shape: torch.Size([20, 1]), Ytrain.shape: torch.Size([20, 1])
Epoch 0: loss=309.5900
Epoch 10: loss=0.3274
Epoch 20: loss=0.2995
Epoch 30: loss=0.2807
Epoch 40: loss=0.2678
Epoch 50: loss=0.2590
Epoch 60: loss=0.2530
Epoch 70: loss=0.2489
Epoch 80: loss=0.2461
Epoch 90: loss=0.2442Linear Model: y = w * x + b
w = 1.989990234375
b = 3.5692780017852783
5. 小结
本节实现了一个最简单的案例:创建一个线性网络模型。
该模型虽然极简,但已经完整包括了 PyTorch 建立模型、模型训练和模型预测的基本步骤。
本文中简化了很多环节,是为了便于读者理解和掌握 PyTorch 深度学习的核心步骤。
【本节完】
版权声明:
欢迎关注『youcans的深度学习』系列,转发请注明原文链接:
【youcans的深度学习 D01】PyTorch例程:极简线性模型
Copyright 2023 youcans, XUPT
Crated:2023-04-18