论文《Pre-training Graph Transformer with Multimodal Side Information for Recommendation》阅读
论文《Pre-training Graph Transformer with Multimodal Side Information for Recommendation》阅读
- 论文概况
- Introduction
- Method
-
- A.Contextual Neighbors Samplin
- B. Node Embedding Initialization
- C. Transformer-based Graph Encode
- D.Model Optimization
- 总结
论文概况
本文是2020年ACMMM 上的一篇论文,通过构建item关系图,寻找项目之间的转化关系,并通过注意力机制与transformer对物品特征进行提取,最终对物品进行预处理。
Introduction
作者提出问题
- 传统的方法是通过人工特征工程来利用物品的多模态信息,它通常需要特定领域的知识,而且很耗时。且现有的解决方案只考虑了特定类型的物品侧面信息,用于专门的推荐应用。项目的全部多模态侧面信息并没有得到充分的利用。
对于上述问题,作者提出了PMGT模型(Pre-tained Multimodal Graph Transformer ):
(1) 构建新型图结构,挖掘物品与物品之间的多模态信息。
(2) 创造MCNSampling算法(Mini-batch Contextual Neighbors Sampling)用于有效且可扩展的训练
(3)采用注意力机制来聚合项目的多模态信息,并采用促进多样性的Transformer框架来模拟一个项目与其在图中的上下文邻居之间的影响。
Method
A.Contextual Neighbors Samplin
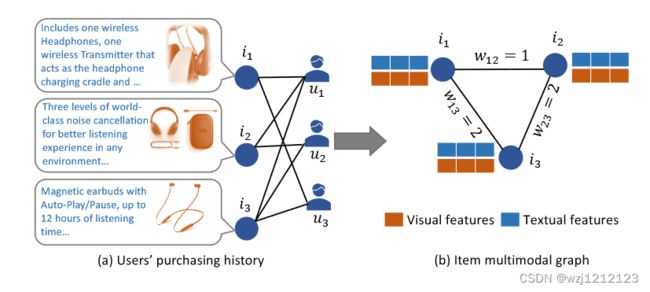 上图是物品关系图的构建方法:同一个用户购买的两个不同的物品会在图中相连,权重是两个物品被一同购买的用户数。
上图是物品关系图的构建方法:同一个用户购买的两个不同的物品会在图中相连,权重是两个物品被一同购买的用户数。
那么对于图中的每个点h,都存在一些可以丰富他们表达的点,我们称之为h的上下文邻居 C h \mathbf{C}_{h} Ch,而h的物理邻居则称为 N h \mathbf{N}_{h} Nh
下面我们将使用MCNSampling算法求出 C h \mathbf{C}_{h} Ch
设初始 C h \mathbf{C}_{h} Ch={h},只包含h本身。下面将 C h \mathbf{C}_{h} Ch每个元素t用 n i \mathbf{n}_{i} ni个点 t ′ 1 , t ′ 2 \mathbf{t'}_{1},\mathbf{t'}_{2} t′1,t′2…替代(i是当前操作的轮数, n i \mathbf{n}_{i} ni是提前设置好的参数), t ′ i \mathbf{t'}_{i} t′i属于 N t \mathbf{N}_{t} Nt,且 t ′ i \mathbf{t'}_{i} t′i=t’的取值概率是t与t’之间在物品图中的权重。然后将上述操作重复K轮,最终得到 C h \mathbf{C}_{h} Ch
我们利用下面的公式来对 C h \mathbf{C}_{h} Ch中每个结点对于h的重要性进行打分:
s t k = f t k × ( K − k + 1 ) (1) s_{t}^{k}=f_{t}^{k} \times(K-k+1)\tag{1} stk=ftk×(K−k+1)(1)
其中 f t k f_{t}^{k} ftk是点t在第K轮 C h \mathbf{C}_{h} Ch中出现的次数,k是轮数,我们可以理解为轮数越少,出现次数越多,则对于h越重要。
最终每个结点的重要程度为:
s t = ∑ k = 1 K s t k (2) s_{t}=\sum_{k=1}^{K} s_{t}^{k}\tag{2} st=k=1∑Kstk(2)
B. Node Embedding Initialization
得到的 C h \mathbf{C}_{h} Ch取重要程度最高的n个点与目标点h组成新的集合S, x t i \mathrm{x}_{t}^{i} xti属于S ,对S中的所有点进行线性变换,并通过注意力机制提取物品特征。
X t i = x t i W M i + b M i , 1 ≤ i ≤ m X t = X t 1 ⊕ X t 2 ⊕ ⋯ ⊕ X t m , α t = softmax [ tanh ( X t ) W s + b s ] , M t = ∑ i m α t i X t i , (3) \begin{array}{c} \mathrm{X}_{t}^{i}=\mathrm{x}_{t}^{i} \mathbf{W}_{M}^{i}+\mathrm{b}_{M}^{i}, 1 \leq i \leq m \\ \mathrm{X}_{t}=\mathrm{X}_{t}^{1} \oplus \mathrm{X}_{t}^{2} \oplus \cdots \oplus \mathrm{X}_{t}^{m}, \\ \alpha_{t}=\operatorname{softmax}\left[\tanh \left(\mathrm{X}_{t}\right) \mathbf{W}_{s}+\mathrm{b}_{s}\right], \mathbf{M}_{t}=\sum_{i}^{m} \alpha_{t}^{i} \mathrm{X}_{t}^{i}, \end{array}\tag{3} Xti=xtiWMi+bMi,1≤i≤mXt=Xt1⊕Xt2⊕⋯⊕Xtm,αt=softmax[tanh(Xt)Ws+bs],Mt=∑imαtiXti,(3)
其中W与b都是可学习变量,然后根据节点在S集合中的位置进行位置向量嵌入(位置越靠前说明对于h来说该节点越重要)
P t = P − Embedding [ p ( t ) ] (4) \mathbf{P}_{t}=\mathbf{P-}\text { Embedding }[p(t)]\tag{4} Pt=P− Embedding [p(t)](4)
再根据节点的角色进行节点角色向量嵌入(就是将S中的原节点h突出,让h在接下来的聚合中取得更大的权重)
R t = R − Embedding [ r ( t ) ] (5) \mathbf{R}_{t}=\mathbf{R}-\text { Embedding }[r(t)]\tag{5} Rt=R− Embedding [r(t)](5)
然后将得到的三个向量嵌入求和,得到S中每个结点的初步向量表示,该向量表示融合了多模态信息、位置信息、角色信息
H t 0 = Aggregate ( M t , P t , R t ) (6) \mathrm{H}_{t}^{0}=\text { Aggregate }\left(\mathrm{M}_{t}, \mathrm{P}_{t}, \mathrm{R}_{t}\right)\tag{6} Ht0= Aggregate (Mt,Pt,Rt)(6)
C. Transformer-based Graph Encode
接下来我们计划通过自注意力机制来提取S的整体特征:
H ℓ = F F N [ softmax ( Q K ⊤ d h ) V ] Q = H ℓ − 1 W Q ℓ , K = H ℓ − 1 W K ℓ , V = H ℓ − 1 W V ℓ , (7) \begin{array}{c} \mathrm{H}^{\ell}=\mathrm{FFN}\left[\operatorname{softmax}\left(\frac{\mathrm{QK}^{\top}}{\sqrt{d_{h}}}\right) \mathrm{V}\right] \\ \mathrm{Q}=\mathrm{H}^{\ell-1} \mathrm{~W}_{Q}^{\ell}, \mathrm{K}=\mathrm{H}^{\ell-1} \mathrm{~W}_{K}^{\ell}, \mathrm{V}=\mathrm{H}^{\ell-1} \mathrm{~W}_{V}^{\ell}, \end{array}\tag{7} Hℓ=FFN[softmax(dhQK⊤)V]Q=Hℓ−1 WQℓ,K=Hℓ−1 WKℓ,V=Hℓ−1 WVℓ,(7)
其中,K、Q、V是可学习参数然而作者认为这种自注意力的做法实际上会损失S中的特征多样性。
因此,在上式基础上我们进行改进
S = H ℓ − 1 W S ℓ , U 1 = softmax ( E − S S ⊤ ∥ S ∥ 2 ∥ S ∥ 2 ⊤ + I ) , (8) \begin{array}{c} \mathrm{S}=\mathrm{H}^{\ell-1} \mathrm{~W}_{S}^{\ell}, \\ \mathrm{U}_{1}=\operatorname{softmax}\left(\mathrm{E}-\frac{\mathrm{SS}^{\top}}{\|\mathrm{S}\|_{2}\|\mathrm{~S}\|_{2}^{\top}}+\mathrm{I}\right), \end{array}\tag{8} S=Hℓ−1 WSℓ,U1=softmax(E−∥S∥2∥ S∥2⊤SS⊤+I),(8)
U 2 = softmax ( Q K ⊤ d h ) , H ℓ = F F N [ ( β U 1 + ( 1 − β ) U 2 ) V ] , (9) \begin{array}{c} \mathbf{U}_{2}=\operatorname{softmax}\left(\frac{\mathrm{QK}^{\top}}{\sqrt{d_{h}}}\right), \\ \mathbf{H}^{\ell}=\mathrm{FFN}\left[\left(\beta \mathbf{U}_{1}+(1-\beta) \mathrm{U}_{2}\right) \mathrm{V}\right], \end{array}\tag{9} U2=softmax(dhQK⊤),Hℓ=FFN[(βU1+(1−β)U2)V],(9)
W S ℓ \mathrm{~W}_{S}^{\ell} WSℓ是可学习参数,E是单位矩阵, S S ⊤ ∥ S ∥ 2 ∥ S ∥ 2 ⊤ \frac{\mathrm{SS}^{\top}}{\|\mathrm{S}\|_{2}\|\mathrm{~S}\|_{2}^{\top}} ∥S∥2∥ S∥2⊤SS⊤其实是在计算S内节点的相似度,相似度越大 U 1 \mathrm{U}_{1} U1权重越小,因此能保留特征多样性。
D.Model Optimization
优化方程:
L edge = 1 ∣ V ∣ ∑ h ∈ V 1 ∣ N h ∣ ∑ t ∈ N h [ − log ( σ ( h ⊤ t ∥ h ∥ 2 ∥ t ∥ 2 ) ) − Q ⋅ E t n ∼ P n ( t ) log ( σ ( − h ⊤ t n ∥ h ∥ 2 ∥ t n ∥ 2 ) ) ] (10) \begin{aligned} \mathcal{L}_{\text {edge }}=& \frac{1}{|\mathcal{V}|} \sum_{h \in \mathcal{V}} \frac{1}{\left|\mathcal{N}_{h}\right|} \sum_{t \in \mathcal{N}_{h}}\left[-\log \left(\sigma\left(\frac{\mathbf{h}^{\top} \mathbf{t}}{\|\mathbf{h}\|_{2}\|\mathbf{t}\|_{2}}\right)\right)\right.\\ &\left.-Q \cdot \mathbb{E}_{t_{n} \sim P_{n}(t)} \log \left(\sigma\left(-\frac{\mathbf{h}^{\top} \mathbf{t}_{n}}{\|\mathrm{~h}\|_{2}\left\|\mathbf{t}_{n}\right\|_{2}}\right)\right)\right] \end{aligned}\tag{10} Ledge =∣V∣1h∈V∑∣Nh∣1t∈Nh∑[−log(σ(∥h∥2∥t∥2h⊤t))−Q⋅Etn∼Pn(t)log(σ(−∥ h∥2∥tn∥2h⊤tn))](10)
L feature = 1 ∣ V ∣ ∑ h ∈ V 1 ∣ M h ∣ ∑ t ∈ M h ∑ i m ∥ H t L W r i − x t i ∥ 2 2 , (11) \mathcal{L}_{\text {feature }}=\frac{1}{|\mathcal{V}|} \sum_{h \in \mathcal{V}} \frac{1}{\left|\mathcal{M}_{h}\right|} \sum_{t \in \mathcal{M}_{h}} \sum_{i}^{m}\left\|\mathrm{H}_{t}^{L} \mathbf{W}_{r}^{i}-\mathrm{x}_{t}^{i}\right\|_{2}^{2} \text {, }\tag{11} Lfeature =∣V∣1h∈V∑∣Mh∣1t∈Mh∑i∑m∥ ∥HtLWri−xti∥ ∥22, (11)
L edge + λ L feature (12) \mathcal{L}_{\text {edge }}+\lambda \mathcal{L}_{\text {feature }}\tag{12} Ledge +λLfeature (12)
(11)就是让最终得到的物品嵌入与各个模态的嵌入不要相差太多,(10)则是让得到的物品嵌入与邻居物品更相似(?)
总结
该文章仍然是通过多模态来对下游模型的物品嵌入做一个预处理,模型中包含很多元素,也挖掘了更多的多模态信息。可以看出有一定工作量,而且方法也可以适用于大多数模型。

