【大数据分析与挖掘】挖掘建模之关联分析
文章目录
- 一、关联规则
-
- 1.1 常用的关联规则算法
- 1.2 Apriori算法介绍
-
- 1.2.1 关联规则与频繁项集
- 1.2.2 Apriori算法的思想与性质
- 1.2.3 Apriori算法的实现的两个过程
- 1.2.4 Apriori算法的实现案例
一、关联规则
关联规则分析也成为购物篮分析,最早是为了发现超市销售数据库中不同的商品之间的关联关系。例如一个超市的经理想要更多地了解顾客的购物习惯,比如“哪组商品可能会在一次购物中同时购买?”或者“某顾客购买了个人电脑,那该顾客三个月后购买数码相机的概率有多大?”他可能会发现如果购买了面包的顾客同时非常有可能会购买牛奶,这就导出了一条关联规则“面包=>牛奶”,其中面包称为规则的前项,而牛奶称为后项。通过对面包降低售价进行促销,而适当提高牛奶的售价,关联销售出的牛奶就有可能增加超市整体的利润。
关联规则分析是数据挖掘中最活跃的研究方法之一,目的是在一个数据集中找出各项之间的关联关系,而这种关系并没有在数据中直接表示出来。
1.1 常用的关联规则算法
1.2 Apriori算法介绍
以超市销售数据为例,提取关联规则的最大困难在于当存在很多商品时,可能的商品的组合(规则的前项与后项)的数目会达到一种令人望而却步的程度。因而各种关联规则分析的算法从不同方面入手减小可能的搜索空间的大小以及减小扫描数据的次数。
Apriori算法是最经典的挖掘频繁项集的算法,第一次实现了在大数据集上可行的关联规则提取,其核心思想是通过连接产生候选项与其支持度然后通过剪枝生成频繁项集。
1.2.1 关联规则与频繁项集
(1)关联规则的一般形式
项集A、B同时发生的概率称为关联规则的支持度:
S u p p o r t ( A − > B ) = P ( A ∪ B ) Support(A->B) = P(A∪B) Support(A−>B)=P(A∪B)
项集A发生,则项集B也同时发生的概率为关联规则的置信度:
C o n f i d e n c e ( A − > B ) = P ( B ∣ A ) Confidence(A->B)=P(B|A) Confidence(A−>B)=P(B∣A)
(2)最小支持度和最小置信度
最小支持度是用户或专家定义的衡量支持度的一个阈值,表示项目集在统计意义上的最低重要性;
最小置信度是用户或专家定义的衡量置信度的一个阈值,表示关联规则的最低可靠性。同时满足最小支持度阈值和最小置信度阈值的规则称作强规则。
(3)项集
项集是项的集合。包含 k 个项的项集称为 k 项集,如集合{牛奶,麦片,糖}是一个3项集。
项集的出现频率是所有包含项集的事务计数,又称作绝对支持度或支持度计数。如果项集 I 的相对支持度满足预定义的最小支持度阈值,则 I 是频繁项集。频繁k项集通常记作 L k L_k Lk 。
(4)支持度计数
项集A的支持度计数是事务数据集中包含项集 A 的事务个数。
已知项集的支持度计数,则规则 A − > B A->B A−>B的支持度和置信度很容易从所有事务计数、项集A和项集 A ∪ B A∪B A∪B 的支持度计数推出:
S u p p o r t ( A − > B ) = A , B 同时发生的事务个数 所有事务个数 = θ ( A ∪ B ) N Support(A->B)=\frac{A,B同时发生的事务个数}{所有事务个数}=\frac{\theta(A∪B)}{N} Support(A−>B)=所有事务个数A,B同时发生的事务个数=Nθ(A∪B)
C o n f i d e n c e ( A − > B ) = P ( A ∣ B ) = θ ( A ∪ B ) θ ( A ) Confidence(A->B)=P(A|B)=\frac{\theta(A∪B)}{\theta(A)} Confidence(A−>B)=P(A∣B)=θ(A)θ(A∪B)
其中 N N N表示事务个数, θ \theta θ表示计数。
1.2.2 Apriori算法的思想与性质
Apriori算法的思想
Apriori算法的主要思想是找出存在于事务数据集中的最大的频繁项集,在利用得到的最大频繁项集与预先设定的最小置信度阈值生成强关联规则。
Apriori算法的性质
频繁项集的所有非空子集也必须是频繁项集。
根据该性质可以得出:向不是频繁项集 I 的项集中添加事务A,新的项集 I ∪ A I∪A I∪A一定也不是频繁项集。
1.2.3 Apriori算法的实现的两个过程
-
找出所有的频繁项集。
在这个过程中连接步和剪枝步互相融合,最终得到最大频繁项集 。 -
连接步
连接步的目的是找到K项集。 -
剪枝步
剪枝步紧接着连接步,在产生候选项 C k C_k Ck 的过程中起到减小搜索空间的目的。
连接步:
(1)对给定的最小支持度阈值,分别对 1 项候选集 C 1 C_1 C1,剔除小于该阈值的的项集得到 1 项频繁集 L 1 L_1 L1;
(2)下一步由自身连接产生 2 项候选集 C 2 C_2 C2 ,保留 C 2 C_2 C2中满足约束条件的项集得到 2 项频繁集,记为 L 2 L_2 L2;
(3)再下一步由 L 1 L_1 L1与 L 2 L_2 L2连接产生 3 项候选集 C 3 C_3 C3,保留 C 3 C_3 C3中满足约束条件的项集得到 3 项频繁集,记为 L 3 L_3 L3。
− − − − − − --- --- −−−−−−
这样循环下去,得到最大频繁项集 L k L_k Lk。
剪枝步:
剪枝步紧接着连接步,在产生候选项 C k C_k Ck的过程中起到减小搜索空间的目的。
由于 C k C_k Ck 是 L k − 1 L_{k-1} Lk−1与 L k − 1 L_{k-1} Lk−1连接产生的,根据Apriori 的性质频繁项集的所有非空子集也必须是频繁项集,所以不满足该性质的项集将不会存在于 C k C_k Ck,该过程就是剪枝。
过程一:找出所有的频繁项集。
过程二:由频繁项集产生强关联规则
由过程一可知未超过预定的最小支持度阈值的项集已被剔除,如果剩下这些规则又满足了预定的最小置信度阈值,那么就挖掘出了强关联规则。
1.2.4 Apriori算法的实现案例
下面将结合餐饮行业的实例来讲解Apriori关联规则算法挖掘的实现过程。数据库中部分点餐数据下表:

首先将上表中的事务数据(一种特殊类型的记录数据)整理成关联规则模型所需的数据结构。从中抽取10个点餐订单作为事务数据集为方便起见将菜品{18491,8842,8693,7794,8705}分别简记为{a,b,c,d,e}),如:

设支持度为0.2,即支持度计数为2,算法过程如下图:
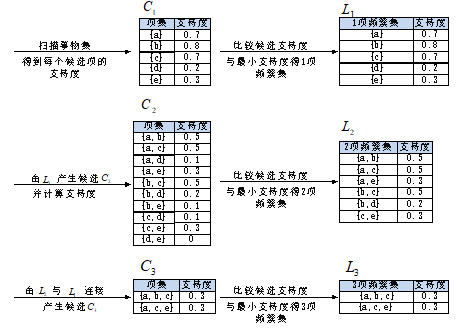
过程一:找最大k项频繁集
- 算法简单扫描所有的事务,事务中的每一项都是候选 1 项集的集合 C 1 C_1 C1的成员,计算每一项的支持度。比如
P ( a ) = 项集 a 的支持度计数 所有事务个数 = 7 10 = 0.7 P({a})=\frac{项集{a}的支持度计数}{所有事务个数}=\frac{7}{10}=0.7 P(a)=所有事务个数项集a的支持度计数=107=0.7 - 对 C 1 C_1 C1中各项集的支持度与预先设定的最小支持度阈值作比较,保留大于或等于该阈值的项,得1项频繁集 L 1 L_1 L1;
- 扫面所有事务, L 1 L_1 L1 与 L 1 L_1 L1连接得候选2项集 C 2 C_2 C2,并计算每一项的支持度。如
P ( a , b ) = 项集 a , b 的支持度计数 所有事务个数 = 5 10 = 0.5 P({a,b})=\frac{项集{a,b}的支持度计数}{所有事务个数}=\frac{5}{10}=0.5 P(a,b)=所有事务个数项集a,b的支持度计数=105=0.5
接下来是剪枝步,由于 C 2 C_2 C2的每个子集(即 L 1 L_1 L1)都是频繁集,所以没有项集从 C 2 C_2 C2中剔除;
-
对 C 2 C_2 C2 中各项集的支持度与预先设定的最小支持度阈值作比较,保留大于或等于该阈值的项,得 2 项频繁集 L 2 L_2 L2;
-
扫描所有事务, L 2 L_2 L2与 L 2 L_2 L2连接得候选 3 项集 C 3 C_3 C3,并计算每一项的支持度,如: P ( a , b , c ) = 项集 a , b , c 的支持度计数 所有事务个数 = 3 10 = 0.3 P({a,b,c})=\frac{项集{a,b,c}的支持度计数}{所有事务个数}=\frac{3}{10}=0.3 P(a,b,c)=所有事务个数项集a,b,c的支持度计数=103=0.3
接下来是剪枝步, L 2 L_2 L2与 L 1 L_1 L1连接的所有项集为:{ a,b,c},{ a,b,d},{ a,b,e},{ a,c,d},{ a,c,e},{ b,c,d},{ b,c,e}。
根据Apriori算法,频繁集的所有非空子集也必须是频繁集,因为{b,d},{b,e},{c,d}不包含在b项频繁集 中,即不是频繁集,应剔除,最后的 L 2 L_2 L2 中的项集只有{ a,b,c}和{ a,c,e};
- 对 C 3 C_3 C3中各项集的支持度与预先设定的最小支持度阈值作比较,保留大于或等于该阈值的项,得3项频繁集 L 3 L_3 L3;
- L 3 L_3 L3与 L 3 L_3 L3 连接得候选 4 项集 ,易得剪枝后为空集。最后得到最大3项频繁集{ a,b,c}和{ a,c,e}。
由以上过程可知 L 3 , L 2 , L 3 L_3,L_2,L_3 L3,L2,L3 都是频繁项集, L 3 L_3 L3是最大频繁项集。
过程二:由频繁集产生关联规则
根据公式:

尝试产生关联规则。
Python程序输出的关联规则如下:


就第一条输出结果进行解释:客户同时点菜品e和a的概率是30%,点了菜品e,再点菜品a的概率是100%。知道了这些,就可以对顾客进行智能推荐,增加销量同时满足客户需求。
