请回答数据结构【栈和队列】

1.栈

1.1 Intro of Stack

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。**进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。**栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

1.1.1 对栈的操作

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

每存入一个数据，栈顶(top)就往上移动一位
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hmTIXExV-1648773291272)(C:\Users\Allen\AppData\Roaming\Typora\typora-user-images\image-20211116115052016.png)]

1.1.2 栈的应用

解决括号匹配问题，逆波兰表达式求解等等，递归改非递归

1.2 两个栈的概念

我们知道了数据结构中的栈，我们也知道操作系统中，虚拟进程地址空间的栈，是内存划分中的一个区域，这两个是一样概念的吗？

当然不是，一个是数据结构一个是用来函数调用时候建立栈帧的，只不过行为类似，是后进先出

1.3 后进先出

对于后进先出的解释，我们有一些练习题

B

C

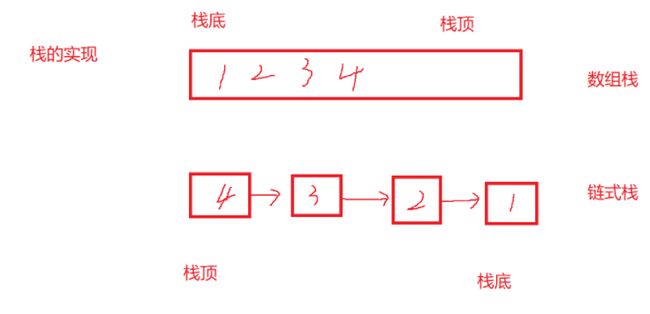
1.4 栈的实现思考

栈是一种特殊的线性表，可以选择一下三种的任意一种实现方法都可以

1. 栈如果选数组作为根本的话，那么扩容成为了问题
2. 如图所示，如果我们要用双向链表完成任务的话，那么栈底先进,反之要用单链表的话就是栈顶，但是能用单链表一般不用双向链表
3. 假设只能选一个，一般选数组，因为栈顶的插入删除效率很高，CPU高速缓存命中率高，增容并不是每次都增容，是偶尔增一下，毕竟单链表也不是不用增容，总体来说命中率高效率肯定高一点

一般情况下栈总归不要求是要遍历的，不然为什么不用顺序表结构呢

1.5 实现数组栈

1.5.0 栈的结构

我们可以用三个变量来定义一个栈的结构，注意容量和栈顶位置的区别

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;		// 栈顶的位置
	int capacity;	// 容量
}ST;

1.5.1 StackInit

初始化一个栈

void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

1.5.2 StackDestory

销毁栈

void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

1.5.3 StackPush

栈数据的插入，由于扩容只会用到一次，所以说其实不哟个单拎出来，直接写在push中就可以了

void StackPush(ST* ps, STDataType x)
{
	assert(ps); 
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		ps->a = (STDataType*)realloc(ps->a, newCapacity* sizeof(STDataType));
		if (ps->a == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->capacity = newCapacity;
	}

	ps->a[ps->top] = x;
	ps->top++;
}

1.5.4 StackPop

void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	--ps->top;
}

1.5.5 StackEmpty

判空，注释掉的写法其实很多余，其实一行就可以完成

bool StackEmpty(ST* ps)
{
	assert(ps);

	/*if (ps->top > 0)
	{
		return false;
	}
	else
	{
		return true;
	}*/
	return ps->top == 0;
}

1.5.6 StackTop

STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);

	return ps->a[ps->top - 1];
}

1.5.7 StackSize

int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

1.5.8 打印栈

while (!StackEmpty(&st))
	{
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");

2. 队列

2.1 Intro of Queue

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出
FIFO(First In First Out)

2.1.1 队列的应用

队列的应用：

公平排队，广度优先遍历

队列思想的应用：

医院、营业厅，抽号机

假如有三个窗口如何保证先来先得到号呢，就是利用队列的性质，前面有多少人排队意味着队列里面含有多少数据,只不过要防止两个人同时取号，如何防止呢，就是利用操作系统当中的互斥锁来解决问题

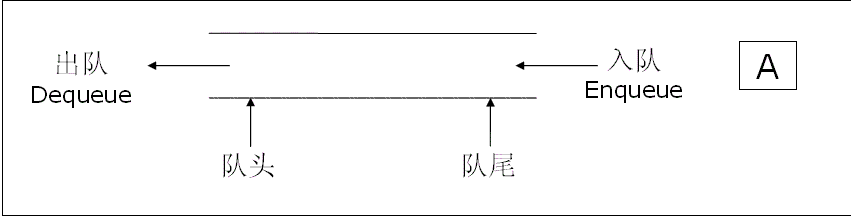
邮局队列的抽象

下面是来自Crash Course Computer Science的对于邮局队列的抽象

2.1.2 队列的操作

入队列：进行插入操作的一端称为队尾

出队列：进行删除操作的一端称为队头

2.2 队列用什么来实现

数组不行，要满足一端入，一端出不太行

链表可以，凡是涉及到链表肯定是能用单链表就单链表，给两个指针，一边入数据，一边出数据，同时记录

尾指针和头指针

2.3 队列的实现

2.3.0 队列结构体

先封装一个Node，然后再构建队列

typedef int QDataType;

typedef struct QueueNode
{
	QDataType data;
	struct QueueNode* next;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	//size_t size;//可以有也可以没有的变量
}Queue;

2.3.1 QueueInit

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

2.3.2 QueueDestory

void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;
}

2.3.3 QueuePush

入列

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	assert(newnode);

	newnode->data = x;
	newnode->next = NULL;

	if (pq->tail == NULL)
	{//the fist node
		assert(pq->head==NULL);
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

2.3.4 QueuePop

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head && pq->tail);

	if (pq->head->next==NULL)
	{// the last node
		free(pq->head);
		pq->head = pq->tail = nullptr;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

2.3.5 QueueEmpty

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	//return pq->head == NULL && pq->tail == NULL;
	return pq->head == nullptr;
}

2.3.6 QueueSize

size_t QueueSize(Queue* pq)
{// slow or a new member variable
	assert(pq);
	QNode* cur = pq->head;
	size_t size = 0;
	while (cur)
	{
		size++;
		cur = cur->next;
	}

	return size;
}

2.3.7 QueueFront

返回队首数据

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);

	return pq->head->data;
}

2.3.8 QueueBack

QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->tail);

	return pq->tail->data;
}

2.4 先进先出

以下( )不是队列的基本运算？/

• 从队尾插入一个新元素
• 从队列中删除第i个元素
• 判断一个队列是否为空
• 读取队头元素的值

B

现有一循环队列，其队头指针为front，队尾指针为rear；循环队列长度为N。其队内有效长度为？(假设队头不存放数据)

• (rear - front + N) % N + 1
• (rear - front + N) % N
• (rear - front) % (N + 1)
• (rear - front + N) % (N - 1)

B

循环队列的存储空间为 Q(1:100) ，初始状态为 front=rear=100 。经过一系列正常的入队与退队操作后， front=rear=99 ，则循环队列中的元素个数为（ ）

• 1
• 2
• 99
• 0或者100

D

3. 小试牛刀

leetcode 有效括号和循环队列https://blog.csdn.net/Allen9012/article/details/121440663

leetcode 栈和队列的互相实现https://blog.csdn.net/Allen9012/article/details/121437192

注：部分图片来源于Crash Course Computer Science，如有侵权请联系我删除