算法篇——层序遍历大集合(js版)
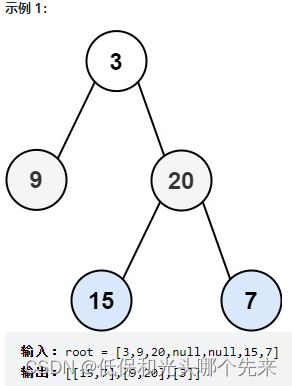
102.二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
链接:力扣
var levelOrder = function(root) {
var res = [], queue = [];
if(!root) return res;
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
for(let i = 0;i < len; i++) {
let node = queue.shift();
curNode.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curNode);
}
return res;
};107.二叉树的层序遍历Ⅱ
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
链接:力扣
var levelOrderBottom = function(root) {
var res = [], queue = [];
if(!root) return res;
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
for(let i = 0;i < len; i++) {
let node = queue.shift();
curNode.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curNode);
}
return res.reverse();
};637.二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
链接:力扣
var averageOfLevels = function(root) {
// res:层序遍历结果数组,avgRes:平均值结果数组,nodeRes:每层节点存储数组
var res = [], queue = [], avgRes = [], nodeRes= [];
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
for(let i = 0;i < len; i++) {
let node = queue.shift();
curNode.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curNode);
nodeRes = res[res.length-1];
var sum = 0
for(var i = 0; i < nodeRes.length; i++) {
sum += nodeRes[i];
}
avgRes.push(sum/nodeRes.length);
}
return avgRes;
};199.二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
链接:力扣
var rightSideView = function(root) {
var res = [], queue = [];
if(!root) return res;
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
for(let i = 0;i < len; i++) {
let node = queue.shift();
curNode.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curNode);
}
var rightRes = [];
for(var i = 0; i < res.length; i++) {
rightRes.push(res[i][res[i].length-1])
}
return rightRes;
};429.N叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
链接:力扣
var levelOrder = function(root) {
var res = [], queue = [];
if(!root) return res;
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
while(len--) {
var cur = queue.shift();
curNode.push(cur.val);
// n叉树不定的节点数,所有不是left,right
for(var i of cur.children) {
i && queue.push(i);
}
}
//把每一层的结果放到结果数组
res.push(curNode);
}
return res;
};515.在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
链接:力扣
var largestValues = function(root) {
var res = [], queue = [], maxRes = [];
// 队列先进先出,层遍历的逻辑
queue.push(root);
while(queue.length && root) {
// 记录当前层级节点数
let len = queue.length;
//存放每一层的节点
let curNode = [];
for(let i = 0;i < len; i++) {
let node = queue.shift();
curNode.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curNode);
nodeRes = res[res.length-1];
var max = nodeRes[0];
for(var i = 0; i < nodeRes.length; i++) {
if(max < nodeRes[i]) {
max = nodeRes[i]
}
}
maxRes.push(max)
}
return maxRes;
};116.填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。
二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。初始状态下,所有 next 指针都被设置为 NULL。
链接:https://leetcode.cn/problems/populating-next-right-pointers-in-each-node
注:单层遍历时记录本层的头部节点,遍历时让前一个节点指向当前节点
var connect = function(root) {
if(root) {
var lcode = root;
while(lcode.left) {
var head = lcode;
while(head) {
head.left.next = head.right;
if(head.next) {
head.right.next = head.next.left;
}
head = head.next;
}
lcode = lcode.left;
}
}
return root;
};或
var connect = function(root) {
if(root) {
var queue = [root];
while(queue.length) {
var len = queue.length;
for(var i = 0; i < len; i++) {
var cur = queue.shift();
if(i < len-1) cur.next = queue[0];
cur.left && queue.push(cur.left);
cur.right && queue.push(cur.right);
}
}
return root;
}
return root;
};117.填充每个节点的下一个右侧节点指针II
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
链接:https://leetcode.cn/problems/populating-next-right-pointers-in-each-node-ii
var connect = function(root) {
if(root) {
var queue = [root];
while(queue.length) {
var len = queue.length;
for(var i = 0; i < len; i++) {
var cur = queue.shift();
if(i < len-1) cur.next = queue[0];
cur.left && queue.push(cur.left);
cur.right && queue.push(cur.right);
}
}
return root;
}
return root;
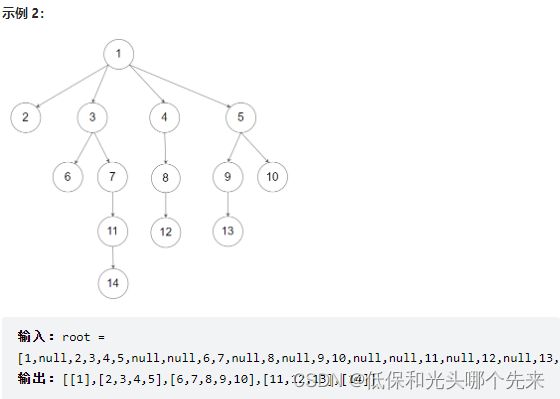
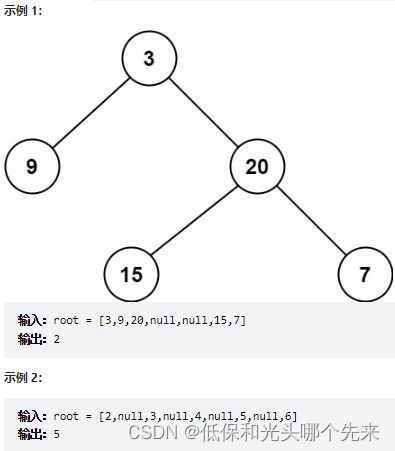
};104.二叉树的最大深度
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3, 9, 20, null, null, 15, 7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree
var maxDepth = function(root) {
if(!root) return 0;
var res = [], queue = [];
queue.push(root);
while(queue.length) {
let len = queue.length;
let curNode = [];
for(let i = 0;i < len; ++i) {
let node = queue.shift();
curNode.push(node.val);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return res.length;
};111.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
链接:力扣
var minDepth = function(root) {
if(!root) return 0;
var queue = [root];
var min = 0;
while(queue.length) {
var len = queue.length;
min++;
for(var i = 0; i < len; i++) {
var cur = queue.shift();
// 没有左右孩子,说明此时是叶子节点,返回min
if(!cur.left && !cur.right) return min;
cur.left && queue.push(cur.left);
cur.right && queue.push(cur.right);
}
}
return min;
};