Gabor 卷积神经网络
与不涉及学习过程的 hand-crafted 滤波器不同，DCNNs-based feature extraction 是一种 data-driven 技术，可以直接从数据中学习具有鲁棒性的特征表示。然而，它有非常大的训练成本和复杂的模型参数。
DCNNs 有限的几何变换建模能力主要来自于大量的数据扩充、大型模型和 hand-crafted 模块。因此如果训练数据不足，它们通常无法处理大型和未知的对象变换。
DCNNs 在一个卷积层的每个位置感受野大小固定的，缺乏处理几何变换的内在机制。
一些工作将Gabor滤波器与DCNNs联系起来。但是，它们没有将 Gabor 滤波器显式地集成到卷积滤波器中。
提出通过传统的 hand-crafted Gabor 滤波器来调制可学习的卷积滤波器，旨在减少网络参数的数量并增强学习特征对方向和尺度变化的鲁棒性
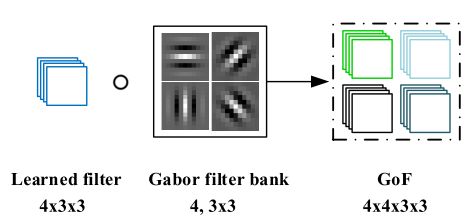
具体来说，在每个卷积层中，卷积滤波器由具有不同方向和尺度的 Gabor 滤波器调制，以产生卷积 Gabor 方向滤波器（GoFs）
与传统的卷积滤波器相比，GoFs 可以捕获输出特征图中的空间定位、方向选择性和空间频率选择性等视觉属性。
GOFS是在CNNS的基础上即卷积滤波器上实现的，因此可以很容易集成到任何深度网络体系结构中。
具有GOFs的DCNNs（称为GCNs)，能够学习更鲁棒的特征表示，特别是对于具有空间变换的图像。 此外，由于GOF是基于一组可学习卷积滤波器生成的，因此GCNS比原始CNN更紧凑，并且具有更少的参数，而不需要模型压缩。
论文主要内容：
- 将 Gabor 滤波器作为调制过程引入卷积滤波器中。 调制滤波器能够增强 DCNNs 对图像变换的鲁棒性，如过渡、尺度变化和旋转；
- GoF 可以很容易地整合到不同的网络架构中；
- 由于Gabor滤波器具有预定义的尺度和方向，所以GCNS可以显著减少可学习滤波器的数量，使网络更加紧凑，同时保持了较高的特征表示能力；
- 提供了在反向传播优化过程中更新 Gabor 方向滤波器的显式推导。
Gabor 卷积网络
将 CNNS 的基本元素卷积滤波器改为 GOFS，以加强 Gabor 滤波器对每个卷积层的影响。 因此，在 DCNNs 中继承了 DCNNs 的方向性，增强了 DCNNs 对尺度和方向变化的鲁棒性。 在反向传播优化中，改进了Gabor方向滤波器的权值。
Gabor 滤波器
Gabor小波（核或滤波器）定义如下: Ψ u , v ( z ) = ∣ ∣ k u , v ∣ ∣ 2 σ 2 e − ( ∣ ∣ k u , v ∣ ∣ 2 ∣ ∣ z ∣ ∣ 2 / 2 σ 2 ) [ e i k u , v z − e − σ 2 / 2 ] . \Psi_{u,v}(z)=\frac {||k_{u,v}||^2} {\sigma^2}e^{-(||k_{u,v}||^2||z||^2/{2\sigma^2})}[e^{ik_{u,v}z}-e^{-\sigma^2/2}]. Ψu,v(z)=σ2∣∣ku,v∣∣2e−(∣∣ku,v∣∣2∣∣z∣∣2/2σ2)[eiku,vz−e−σ2/2].其中 z = ( x , y ) , k u , v = k v e i k u , k v = ( π / 2 ) / 2 ( v − 1 ) , k u = u π U , w i t h v = 0 , . . . , V , u = 0 , . . . , U z=(x,y),k_{u,v}=k_ve^{ik_u},k_v=(\pi/2)/\sqrt{2}^{(v-1)},k_u=u\frac \pi U,with\space v=0,...,V,u=0,...,U z=(x,y),ku,v=kveiku,kv=(π/2)/2(v−1),ku=uUπ,with v=0,...,V,u=0,...,U ， v v v 是频率， u u u 是方向。
GoFs
Gabor 卷积有 U 个方向和 V 个尺度。
将方向信息编码在可学习滤波器中，同时将尺度信息嵌入到不同的层中，从而将 The Steerable Properties 融入到 GCNS 中。
由于 Gabor 滤波器在 GOFS 中捕获了方向和尺度信息，从而增强了相应的卷积特征。
与标准CNNs（标准CNNs中的卷积滤波器采用反向传播(BP)算法学习）不同，用于对方向信道进行编码，GCNs中的可学习滤波器是三维的。
设可学习过滤器的大小为 N × W × W N\times W\times W N×W×W，其中 W × W W\times W W×W 是滤波器的大小，N 指的是通道。
在可学习滤波器上使用 U 个 Gabor滤波器给定 V 个尺度 ，基于调制过程获得GOF。
对于 v 个尺度： C i , u v = C i , o ∘ G ( u , v ) C_{i,u}^v=C_{i,o}\circ G(u,v) Ci,uv=Ci,o∘G(u,v)其中， C i , o C_{i,o} Ci,o 是可学习滤波器， G ( u , v ) G(u,v) G(u,v) 表示一组不同方向和尺度的 Gabor 滤波器。 ∘ \circ ∘ 是 G ( u , v ) 2 G(u,v)^2 G(u,v)2与 C i , o C_{i,o} Ci,o 的每个2D滤波器之间的逐元素乘积运算。在每个尺度下，GOF的大小为 U × N × W × W U×N×W×W U×N×W×W。 由于Gabor滤波器是给定的，所以只节省了 N × W × W N×W×W N×W×W 的可学习滤波器，这意味着我们可以在不增加参数数的情况下通过这种调制获得增强的特征。
GCN卷积
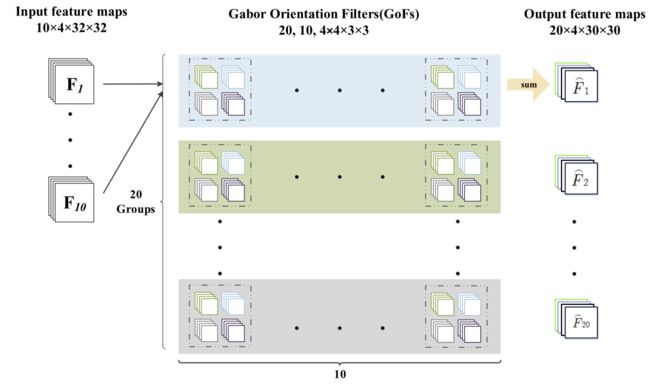
在GCNS中，GOFS用于生成特征映射，显式地增强了深度特征中的尺度和方向信息。 一个在 GCNs 中的输出特征映射 F ^ \hat F F^ 为： F ^ = G C c o n v ( F , G i ) , \hat F=GCconv(F,G_i), F^=GCconv(F,Gi), 其中 C i C_i Ci 是第 i i i 个 GOF ， F F F 是输入特征映射。
通道的 F ^ \hat F F^ 可以通过卷积得到： F ^ = ∑ n = 1 N F ( n ) ⊗ C i , u = k ( n ) , \hat F=\sum_{n=1}^{N}F^{(n)}\otimes C_{i,u=k}^{(n)}, F^=n=1∑NF(n)⊗Ci,u=k(n),其中 n n n 指的是第 n n n 个通道的 F F F 和 C i , u C_{i,u} Ci,u， F ^ i , k \hat F_{i,k} F^i,k 是 F ^ \hat F F^ 的第 k k k 个方向响应。
如果有10个具有4个 Gabor 方向的 GOFs，则输出特征图的大小为 10×4×30×30。
输入特征映射扩展到多通道时 GCNs 的前向卷积过程( C i , n ≠ 1 C_{i,n}\not = 1 Ci,n=1 ) ：
更新GOF
与传统CNNs不同的是，GCNs中前向计算涉及的权值为GOFs，而保存的权值仅为学习后的滤波器。因此，在反向传播（BP）过程中，只需要更新可学习的滤波器 C i , o C_{i,o} Ci,o。
将GOFS中子滤波器的梯度加到相应的可学习滤波器上： δ = ∂ L ∂ C i , o = ∑ u = 1 U ∂ L ∂ C i , u ∘ G ( u , v ) C i , o = C i , o − η δ , \delta=\frac{\partial L}{\partial C_{i,o}}=\sum_{u=1}^{U}\frac {\partial L}{\partial C_{i,u}} \circ G(u,v)\\C_{i,o}=C_{i,o}-\eta\delta, δ=∂Ci,o∂L=u=1∑U∂Ci,u∂L∘G(u,v)Ci,o=Ci,o−ηδ,其中 L L L 是损失函数。通过对学习到的卷积滤波器 C i , o C_{i,o} Ci,o 进行更新，使得GCNS模型更加紧凑、高效，并且对方向和尺度变化具有更强的鲁棒性。
GCNS中第一个卷积层的可视化:
每一行表示一组GOF及其对应的特征映射，例如第10个GOFs ( C 10 , 1 , . . . , C 10 , 4 ) (C_{10,1},...,C_{10,4}) (C10,1,...,C10,4)。
每个 4 方向通道GOF被标记为不同的颜色。 输出的特征映射也有 4 方向通道，并用与其对应的GOF相同的颜色标记。 蓝色矩形中的示例表明GOFS携带各种方位信息
实现
GCNs 的实现基于传统的 CNNs 和 ResNet 架构。
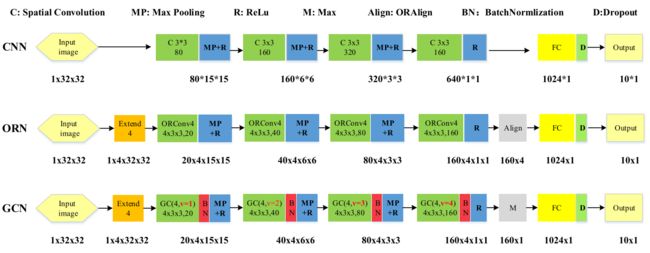
CNN、ORN 和 GCN 的网络结构：
用于resnet的残差块 (a)和(b)，用于GCNS的 ( c )小内核和(d)大内核（尺寸越大的核携带的Gabor方向信息越多）：
论文用基于GoFs的GCConv层替换了空间卷积层，从而得到了GCN-ResNet。