【图-注意力笔记，篇章1】Graph Transformer：包括Graph Transformer 的了解与回顾且其与GNN、Transformer的关联

说明：本文仅供学习，未经同意请勿转载
笔记时间：2022年08月
博客公开时间：2023年2月27日

篇章1先从看看目前Graph注意力中比较火的方法吧，也就是Graph 与Transformer的结合。那Graph Tranformer与GNN和Transformer之间的区别与关联是怎么样的呢？下面让笔者我一一述来。（如果观点/理解存在不对的，欢迎指正。）

GNN、Transformer与Graph Transformer的关系?

在讲的Graph Transformer的相关论文前，我们先直观地来理解一下GNN与Transformer之间的关系是什么。

GNN与Transformer的关系

1. 从连接结构的角度看

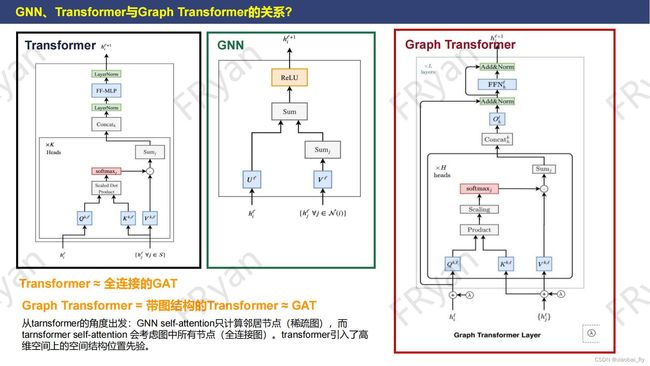
我们知道Transformer最初是来源于NLP领域，其使用注意力机制来构建每个单词的特征，比如右上橙色图，找到句子中其他单词对前面当前单词的重要程度，基于此，Transformer就可以根据该重要程度，对其他所有单词进行加权的线性变换，以此更新当前单词的特征。从右上红色的单词关注来看，我们可以很清晰的明白，Transformer中，当前单词 关注其他所有 的单词，是一种全局的揽括，从图的角度上来看就是一种全连接的状态。

2.从公式的角度看

$\cdot$ Transformer的简单介绍

(对Transformer熟悉的可以直接跳过这一部分阅读)

Transformer的一大重点在于其利用Q（查询）= $Q^l{H}^l$，K（键）= $K^l{H}^l$，V（键值）= $V^l{H}^l$，三个张量来构建注意力机制。结合上面结构的例子，从左边公式来看：就是用当前单词$h_i^l$作为查询值$Q{h}_i^l$【注意：这里一般需要通过$Q$对$h_i^l$做一个线性变换才能得查询值$Q{h}_i^l$，比如我们要查询Transformer这篇文章，这篇文章的特征可能是[Attention,Transformer，NLP]，但是我们做查询时输入可能就只有Transformer这个关键字，所以查询值并不是文章本身的特征】，来查询句子里单词对我的贡献是多少? 而其他单词的关键词（键）就是它们自身的特征$h_j^l,j\in S$（ 这里同样需要对关键词做线性变换得到键$K^l{h}_j^l,j\in S$， 理由同上）。那怎么得到其他单词对当前单词的贡献（注意力分数）呢？可以从搜索引擎的角度上来理解：比如我们在搜索文献时，输入查询值（深度学习，Transformer），那么搜索系统会根据文章的关键词返回搜索结果。因此，实际上就是输入的查询值与文章的关键词的相似性计算，越相似的就会排在越前面，也就是贡献越大，重要程度越大。因此，我们可以通过关键词和查询值之间的点积得到注意力分数$w_{ij}:=softam{x}_j(Q^l{h}_i^l\cdot K^l{h}_j^l)$。当然搜索引擎还有会考虑文献自身的重要性，比如引用量/点击量，在相同注意力分数的情况下，应该把更好的文献排在前面。其中，文献的引用量，点击量等都可以看出文献本身的特征。因此，得到注意力分数之后，我们需要对对键值进行加权求和，才能得到与当前查询值更匹配的特征$h_i^{l+1}:=\delta ({\sum }_{j\in S}{w}_{ij}(V^l{h}_j^l))$。

$\cdot$ 简单地介绍一下GNN

(对GNN熟悉的可以直接跳过这一部分阅读)

GNN和GCN们的重点就是它们考虑了数据结构本身的拓扑属性，可以处理非欧式空间数据。基于所构建Graph，GNN和GCN们可以通过 aggregate（聚合）邻居节点们 $N(i)$的特征$\{h_j^l|j\in N(i)\}$来更新当前的中心节点$i$的特征$h_i^l$。除了考虑邻居节点的特征，自身本来的特征也是十分重要的（从社交网络的角度看，就是你不能只看群体关系，每个人自身本身也是一个独特的存在，哈哈），所以在更新节点特征的时候要同时考虑自身和邻居节点，即$h_i^{l+1}:=\delta (U^l{h}_i^l+{\sum }_{j\in N(i),i\ne j}(V^l{h}_j^l))$。比如紫色的图中，This节点可以通过聚合与它相连接的is，a , sentence, also的节点单词特征来更新This本自身的特征 （当然还有自环，上面的图没有画出来）。其他单词的更新也是如此。基于此，节点的特征就能够在整个图中进行传播。在现实中，我们的Graph一般不是全连接图，上面给出的示例仅是为跟Transformer对比。

$\cdot$ GNN与Transformer的公式对比

根据前面的介绍，GNN节点的更新$h_i^{l+1}:=\delta (U^l{h}_i^l+{\sum }_{j\in N(i)}(V^l{h}_j^l))$实际上整理一下就可以变成 $h_i^{l+1}:=\delta ({\sum }_{j\in \{N(i),i\}}(A^l{h}_j^l))=\delta ({\sum }_{j\in S=\{N(i),i\}}(A^l{h}_j^l))$。同样，Transformer的公式整理一下也可以变成 $h_i^{l+1}:=\delta ({\sum }_{j\in S}(A^l{h}_j^l))$。因此，两者公式实际上是类似的。当Graph是全连接图时，那么GNN的节点公式实际上等同于Transformer的节点公式（因为Transformer关注每一个单词对当前单词的影响）。因此，Transformer实际上就是可以看成全连接的GAT。

Graph Transformer是什么 & 关联？

我们都知道Transformer实际上就是关注到全局的Attention，而且Transformer实际上就是可以看成全连接的GAT，那么Graph Transformer是什么？为什么会有Graph Transformer ? 它跟GAT的区别是什么？

1. Graph Transformer是什么

先简单的回答一下第一个问题，Graph Transformer实际上就是带图结构的Transformer，其近似于GAT。

2. Graph Transformer与GAT， Transformer之间的区别/关联

既然是近似，那Graph Transformer与GAT， Transformer之间的区别是什么?
从Attention机制的角度来简单的回答一下第三个问题。GAT们的self-attention只计算邻居节点，而Transformer们的self-attention会考虑所有的节点 。相对Graph Transformer的全连接图（稠密图），GAT中的Graph可以看成一种相对稀疏的图（不一定全连接）。对比于Transformer，Graph Transformer在Transformer的基础上引入图的拓扑结构属性，使模型有高维空间上的结构位置先验。因此，Graph Transformer结合了Transformer的核心（全局关注）和GNN的核心（考虑图的拓扑属性）。

说明：上面PPT的三个结构图来源于论文《A Generalization of Transformer Networks to Graphs》 (DLG-AAAI 2021)

3. 为什么会有Graph Transformer

根据前面的介绍，我们知道Graph Transformer可以集合GNN和Transformer的核心优点，这也是为什么会有Graph Transformer的出现。存在必然有理，存在必有局限！下面简单介绍一下Graph Transformer存在的理由（带来的好处）和局限性。

$\cdot$ 相对GNN、GAT的优缺点对比

1. 优点

• 相比GAT，Graph Transformer具有更大的表征的能力，在处理图形数据时能够捕获节点之间的复杂关系，而GAT则是使用了一种局部邻居聚合的方式。
• 相比GAT，Graph Transformer对于缺失节点和边的情况处理能力更强。
• 相比GNN，具有捕获长距离依赖的优点。
• 相比GNN，Transformer结构的引入可以缓解GNN中message passing引起的over-smoothing（过平滑）和over-squashing（过挤压）现象。（这个后面会简单介绍）
• 相比GNN，可以通过[CLS] token的利用去除/减少pooling function的使用。
• 相比GNN，Graph Transformer能够高效地处理大规模图形数据，包括超过数百万个节点和边的图形数据。这是由于Transformer模型的并行处理能力，以及Graph Transformer采用的自注意力机制，使得每个节点只需关注其邻居节点，而非整个图形。

2. 缺点

• 相比GAT，Graph Transformer的局部关注能力相对较差些（但是后来基于Graph Transformer的研究改善了一局限，这也是最后一点优点罗列的原因）。
• 相比GNN，Graph Transformer由于模型复杂度高，需要大量的训练数据才能发挥其优势等原因，在处理简单的图形数据/小数据集时可能表现不如GNN。
• 相比GNN，Graph Transformer的性能高度依赖于图形结构的特征，如图形密度、大小、节点度数分布等。对于结构差异较大的图形数据，可能需要使用其他的图神经网络模型进行处理。

$\cdot$ 相对Transformer的优缺点对比

1. 优点

• 相比Transformer，Graph Transformer引入了图的拓扑结构，可以结合GNN及其频域的信息（Laplacian PE）。比如频率上的图模型加Transformer。因此，Graph Transformer可以用于处理图形数据，而Transformer则更适用于序列数据。
• 相比Transformer，Graph Transformer在图形数据建模方面具有强大的表征能力，能够捕获节点之间的复杂关系（比如异构图Graph Transformer模型），并且能够处理不同类型的节点和边。
• 相比Transformer，Graph Transformer能够高效地处理大规模图形数据。

2. 缺点

• 相较于Transformer，Graph Transformer在处理序列数据时可能表现不如Transformer。
• 相比Transformer/GNN，Graph Transformer的计算复杂度较高，需要较大的内存和计算资源来进行训练和推断。

Graph Transformer的简单回顾

简单地了解Graph Transformer的相关信息及优劣势后，下面笔者将简单的对当前Graph Transformer模型进行一个简单的回顾。

早期的Graph Transformer

早期的Graph Transformer = GNN concat Transformer
早期的Graph Transformer主要是类似于将GNN和Transformer级联起来（从右下角模型可以清楚看出）。比如下面两篇论文：【Self-Supervised Graph Transformer on Large-Scale Molecular Data (NeurIPS 2020)】和【GraphTrans：Representing Long-Range Context for Graph Neural Networks with Global Attention (NeurIPS 2021)】
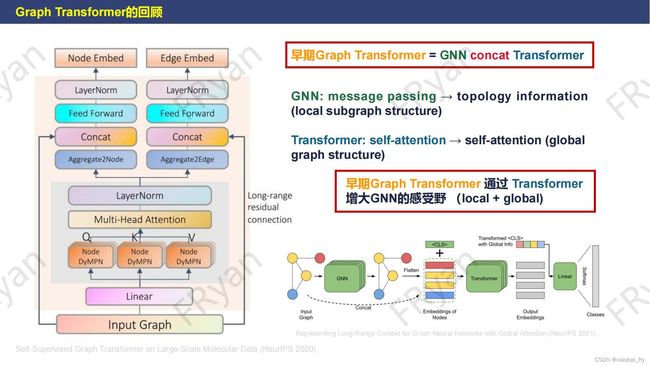在GNN中，我们通过message passing （节点信息传播）可以捕获到图中的局部结构信息（local）；而在Transformer中，我们可以通过因此将数据先通过self-attention获取全局信息（global）。为集合GNN和Transformer这两个优点，早期的Graph Transformer先经过GNN的message passing捕获节点的局部信息特征表征，基于此，进一步通过线性变换得到Transformer中Q，K，V。因此，此时的Q，K，V均带有局部结构（local subgraph structure）信息。最后，在Transformer的self-attention下获取global信息。综上，早期简单的Graph Transformer模型就诞生啦。

上面两篇论文模型值得关注的点：
（1）与大多数GNN类似，上图左边的Graph Transformer模型为了进一步防止 message passing 出现 over-smoothing 现象，将残差链接变成了 long-range residual connection（类似跳跃连接，JK-Net【论文链接】），也就是直接将原始特征接到后面。

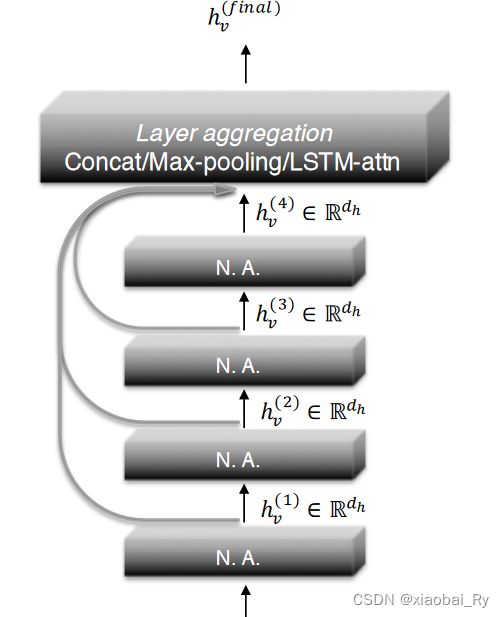
(2)上图右下角的GraphTrans模型提出了一种新的ReadOut机制。这种机制实际上就是NLP或者说VIT模型【论文链接】中的 [CLS] token。（VIT中[CLS] token的引入也同样来源于NLP）

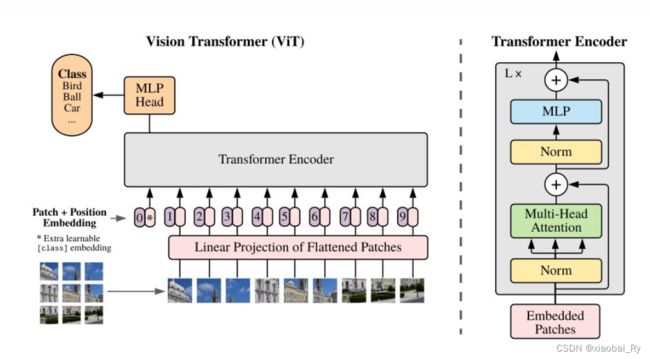
这种 [CLS] token的引入 跟Vision Transformer的构想是一样的，对Graph Transformer的学习是重要的。要知道Graph和图像一样应该是要具有排列不变性（permutation-invariant）的，比如Vision GNN【论文链接】。

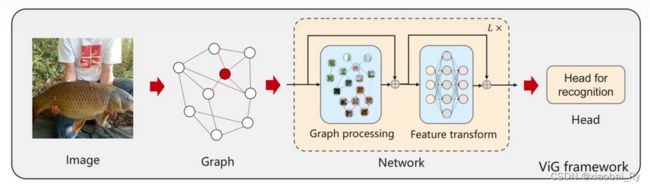
而且Graph比起图像的话，其对同阶节点的聚合的排列不变性应该是更加严格的。图像虽然说考虑排列不变性，但相比Graph的话，其位置还是有影响的（尤其是对分类/非目标检测问题的话）。但是如果像NLP中Transformer一样加上位置编码（PE) 可能就没有办法实现节点聚合的排列不变性了。因此，[CLS]的引入是值得关注的点。

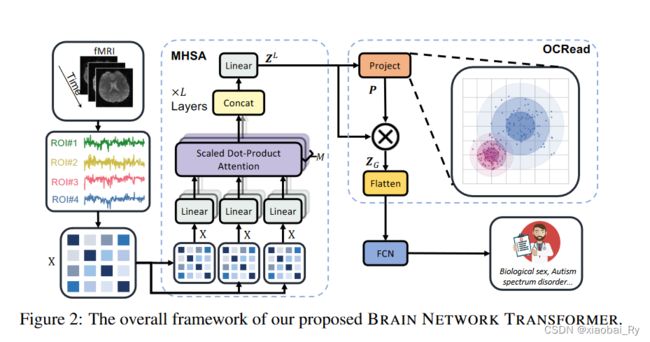
还有的研究是结合各种PE和最后用一个聚类的ReadOut来实现不同节点的关注，笔者感觉基于聚类/分类的ReadOut的机制跟上面[CLS]的引入是异曲同工之妙。比如Brain Network Transformer这篇论文 【论文链接】。

早期Graph Transformer的进阶1

早期Graph Transformer的进阶1：改善结构信息的关注
为了改善对局部结构信息的保留与学习（特别随着网络加深，这种局部结构的保留更少），下面Structure-Aware Transformer模型【论文链接】通过k-hop子图来保留更多的局部信息。虽然网络结构类似于前面的GraphTrans模型，但Structure-Aware Transformer是子图输入，使用PE，而GraphTrans是图输入，使用[CLS]。
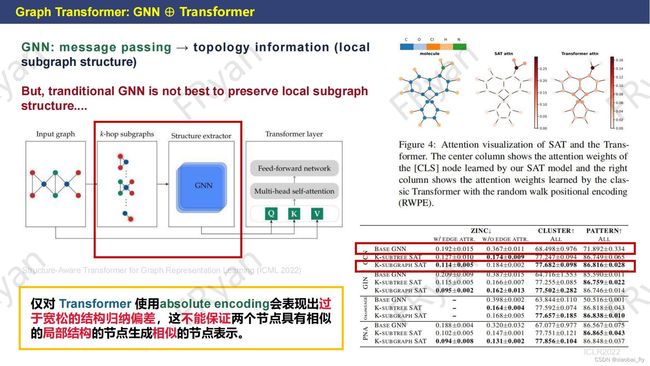要知道，即使使用PE，Transformer 生成的节点表示不一定捕获节点之间的结构相似性（比如右上的可视化），而且其依赖于图结构特征的输入。因此，Structure-Aware Transformer在Transformer之前先利用子图来提取特征。这样子就可以融合子图的局部结构信息。也有比较多关于结构保留这方面研究的工作，如果感兴趣，可以自行检索阅读。

早期Graph Transformer的进阶2

早期Graph Transformer的进阶2：添加边/关系信息，考虑异构性
为了揽括更多丰富的信息，基于Graph Transformer的研究还引入了类似PE（位置编码）、RE（关系编码）、SE（结构编码）等的编码信息。这三种编码是笔者认为比较重要的。下面左边的论文【论文链接】引入边的特征，右上的论文是一篇引用在骨架【机器人，智能体形态】上的论文【论文链接】，使用了位置编码和关系编码，考虑了Graph结构中复杂的关系，下面的论文【论文链接】则是介绍了不同位置编码的方式及其影响。在笔者阅读的相关文献中，笔者发现多数的研究会把边特征和关系特征融合到attention机制里，以此来获取对复杂关系的关注与学习。
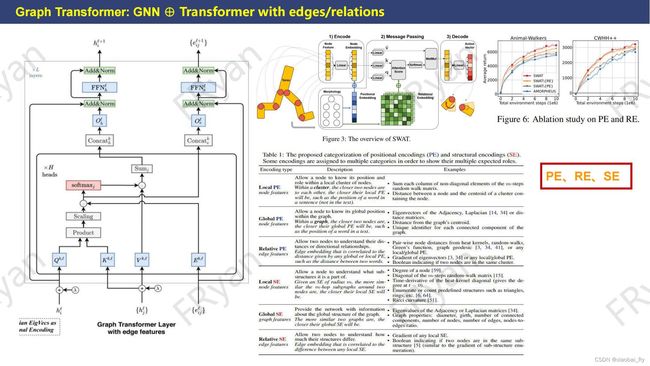因此，从上面的PPT可以看出，实际上Graph Transformer的算法优化类似于Transformer的优化【如何设计更好，更有效的PE编码】/GNN的优化【如何假定更好的图，考虑异构性，考虑边特征等】，以及两者之间怎么更好的结合【如何利用结构信息、连接矩阵、关系来改善注意力机制】。

两篇经典Graph Transformer来入门之预告版

由于文章篇幅有点过长，对上述两篇文章的分享将在新的一期【图-注意力笔记，篇章2】中分享，这里先做个【图-注意力笔记，篇章2】笔记公开的预告吧。虽然这两篇文章思路非常清晰，介绍也相对比较简要，但是笔者认为是Graph Transformer中值得一读的经典文献吧。而且从论文本身的框架图就可以非常清楚的知道两者对GNN与Transformer的结合机制是不一样。

2023年3月2日已更新【图-注意力笔记，篇章2】Graphormer 和 GraphFormers论文笔记之两篇经典Graph Transformer来入门，点击上面可跳转。

好文推荐及相关参考链接

• 想要快速了解更多Graph Transformer的，建议可以读一下《一文带你浏览Graph Transformers 》博客
• 《Transformers是一种图神经网络 》