排序——选择排序

    在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数其中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比較为止。
程序流程：
第一趟，从n 个记录中找出关键码最小的记录与第一个记录交换；
第二趟，从第二个记录開始的n-1 个记录中再选出关键码最小的记录与第二个记录交换；
以此类推.....

第i 趟，则从第i 个记录開始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换，直到整个序列按关键码有序。

程序例如以下：

#include <iostream>
using namespace std;
    
void print(int a[], int n ,int i) /*打印出当前数组中的值*/
{  
    int j;

	cout<<"第"<<i+1 <<"次 : ";  
    for(j= 0; j<8; j++)
	{  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl;  
}  

void select_sort(int a[], int n)
{  
    int tmp, i;
	int index, min_index;

    for(i=0; i < n; ++i) /*选择每次应该放在下标为i的单元的数*/ 
	{  
        for(index=i, min_index=i; index < n; index++) /*找出从当前i到数组末尾的最小值*/
		{
			if(a[index] < a[min_index])
				min_index = index;
		}

        if(min_index != i) /*假设查找到下标不是起始下标，做交换*/
		{  
            tmp = a[i];  
			a[i] = a[min_index]; 
			a[min_index] = tmp;  
        }  
        print(a,  n , i); /*打印出这步进行完的结果*/  
    }  
}  
int main()
{  
    int a[8] = {3, 1, 5, 7, 2, 4, 8, 6};
	
    cout<<"初始值：";  
    for(int j= 0; j < 8; j++){  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl<<endl;  
    select_sort(a, sizeof(a)/sizeof(int));  
	
	return 0;
}  

程序执行结果：

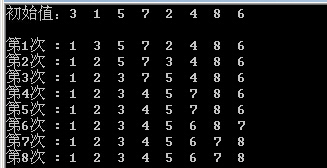
选择排序的特点：

时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：不稳定，举个简单的样例来说明一下，有序列3, 3, 4, 1, 5使用选择排序实现排序，那么首先位置1的3就会和位置4的1进行交换，那么原来位置1和位置2的两个3的相对位置就发生了变化，这样的情况就可能导致终于两个3的前后位置发生了变化。

分析：这个排序的过程每次仅仅选取了最大或最小值中的一个，为了提高效率，我们能够每次选择出最大和最小的值并分别放在序列的头部和尾部，这样实现排序更优于上面的作法。这样实现的代码和执行结果例如以下所看到的：

#include <iostream>
using namespace std;
    
void print(int a[], int n ,int i) /*打印出当前数组中的值*/
{  
    int j;

	cout<<"第"<<i+1<<"次： "; 
    for(j= 0; j<n; j++)
	{  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl;  
}  

void select_sort(int a[], int n)
{  
    int tmp1, tmp2, i, j;
	int index, min_index, max_index;

    for(i=0; i < n/2; ++i)
	{  
        for(index=i, min_index=i, max_index=n-1-i; index < n-i; index++) /*找出从当前i到数组末尾的最小值和最小值*/
		{
			if(a[index] < a[min_index])
				min_index = index;
			if(a[index] > a[max_index])
				max_index = index;
		}

        if(min_index != i) /*假设查找到下标不是起始下标，做交换*/
			               /*第一个数的交换不会出现故障*/
		{  
            tmp1 = a[i];  
			a[i] = a[min_index]; 
			a[min_index] = tmp1;  
        }

		if(max_index != n-i-1) /*第二步的交换假设须要交换的坐标是i就会出问题*/
		                       /*由于此刻i处的值可能已经改变*/
		{
			if(max_index != i)
			{
				tmp2 = a[n-1-i];
				a[n-1-i] = a[max_index];
				a[max_index] = tmp2;
			}
			else
			{
				a[n-1-i] = tmp1;
			}
		}
        print(a,  n , i); /*打印出这步进行完的结果*/  
    }  
}  
int main()
{  
    int a[] = {3, 1, 5, 7, 2, 4, 8, 6, 9};
	
    cout<<"初始值：";  
    for(int j= 0; j < sizeof(a)/sizeof(int); j++){  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl<<endl;  
    select_sort(a, sizeof(a)/sizeof(int));  
	
	return 0;
}  

程序执行结果截图：

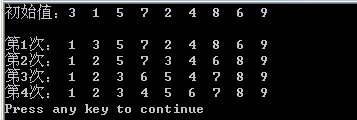
注意：同一时候找出最大值和最小值的方法，在做交换的时候尤其须要注意，由于交换的时候假设两个交换有交叉的话easy出错，详见程序中的凝视。