unity之uv贴图画圆弧,圆弧面,不规则图形
由于最近一直没有时间,所以这篇博客一直没发,下面我说说uv画圆弧,圆面,不规则面拼接。
先来两张效果图
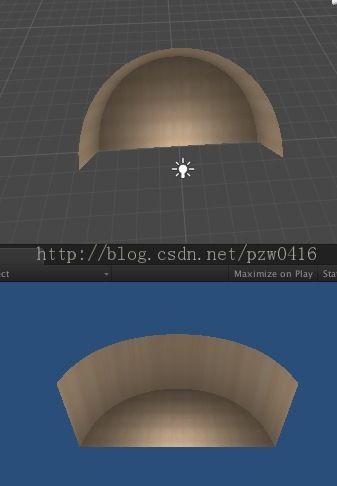
图截的不咋滴,凑合着看吧,画圆弧主要用的贝塞尔曲线画的,我感觉这个比较简单,当然大家也可以使用圆的方程,抛物线的方程都可以实现这种效果
但是我比较倾向于用贝塞尔,如果大家会ps的话,知道里边有一个钢笔工具,他就是贝塞尔的原理,贝塞尔的算法大家可以去网上搜搜,
贝塞尔计算方法类网上也有很多
下面先上我的代码
using UnityEngine;
[System.Serializable]
public class Bezier : System.Object
{
public Vector3 p0;
public Vector3 p1;
public Vector3 p2;
public Vector3 p3;
public float ti = 0f;
private Vector3 b0 = Vector3.zero;
private Vector3 b1 = Vector3.zero;
private Vector3 b2 = Vector3.zero;
private Vector3 b3 = Vector3.zero;
private float Ax;
private float Ay;
private float Az;
private float Bx;
private float By;
private float Bz;
private float Cx;
private float Cy;
private float Cz;
public Bezier( Vector3 v0, Vector3 v1, Vector3 v2, Vector3 v3 )
{
this.p0 = v0;
this.p1 = v1;
this.p2 = v2;
this.p3 = v3;
}
// 0.0 >= t <= 1.0
public Vector3 GetPointAtTime( float t )
{
this.CheckConstant();
float t2 = t * t;
float t3 = t * t * t;
float x = this.Ax * t3 + this.Bx * t2 + this.Cx * t + p0.x;
float y = this.Ay * t3 + this.By * t2 + this.Cy * t + p0.y;
float z = this.Az * t3 + this.Bz * t2 + this.Cz * t + p0.z;
return new Vector3( x, y, z );
}
private void SetConstant()
{
this.Cx = 3f * ( ( this.p0.x + this.p1.x ) - this.p0.x );
this.Bx = 3f * ( ( this.p3.x + this.p2.x ) - ( this.p0.x + this.p1.x ) ) - this.Cx;
this.Ax = this.p3.x - this.p0.x - this.Cx - this.Bx;
this.Cy = 3f * ( ( this.p0.y + this.p1.y ) - this.p0.y );
this.By = 3f * ( ( this.p3.y + this.p2.y ) - ( this.p0.y + this.p1.y ) ) - this.Cy;
this.Ay = this.p3.y - this.p0.y - this.Cy - this.By;
this.Cz = 3f * ( ( this.p0.z + this.p1.z ) - this.p0.z );
this.Bz = 3f * ( ( this.p3.z + this.p2.z ) - ( this.p0.z + this.p1.z ) ) - this.Cz;
this.Az = this.p3.z - this.p0.z - this.Cz - this.Bz;
}
// Check if p0, p1, p2 or p3 have changed
private void CheckConstant()
{
if( this.p0 != this.b0 || this.p1 != this.b1 || this.p2 != this.b2 || this.p3 != this.b3 )
{
this.SetConstant();
this.b0 = this.p0;
this.b1 = this.p1;
this.b2 = this.p2;
this.b3 = this.p3;
}
}
}
这就是贝塞尔计算类,很简单的计算方法,
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
public class TriangleSubdivision :MonoBehaviour{
public static int[] TriangulatePolygon (Vector2[] XZofVertices) {
//
int VertexCount = XZofVertices.Length;
//minx miny maxx maxy
float xmin = XZofVertices[0].x;
float ymin = XZofVertices[0].y;
float xmax = xmin;
float ymax = ymin;
for (int ii1 = 1; ii1 < VertexCount; ii1++)
{
if (XZofVertices[ii1].x < xmin)
{
xmin = XZofVertices[ii1].x;
}
else if (XZofVertices[ii1].x > xmax)
{
xmax = XZofVertices[ii1].x;
}
if (XZofVertices[ii1].y < ymin)
{
ymin = XZofVertices[ii1].y;
}
else if (XZofVertices[ii1].y > ymax)
{
ymax = XZofVertices[ii1].y;
}
}
float dx = xmax - xmin;
float dy = ymax - ymin;
float dmax = (dx > dy) ? dx : dy;
float xmid = (xmax + xmin) * 0.5f;
float ymid = (ymax + ymin) * 0.5f;
Vector2[] ExpandedXZ = new Vector2[3 + VertexCount];
for (int ii1 = 0; ii1 < VertexCount; ii1++)
{
ExpandedXZ[ii1] = XZofVertices[ii1];
}
ExpandedXZ[VertexCount] = new Vector2((xmid - 2 * dmax), (ymid - dmax));
ExpandedXZ[VertexCount + 1] = new Vector2(xmid, (ymid + 2 * dmax));
ExpandedXZ[VertexCount + 2] = new Vector2((xmid + 2 * dmax), (ymid - dmax));
List<Triangle> TriangleList = new List<Triangle>();
TriangleList.Add(new Triangle(VertexCount, VertexCount+1, VertexCount+2));
for (int ii1 = 0; ii1 < VertexCount; ii1++)
{
//检查构成的三角形
List<Edge> Edges = new List<Edge>();
for (int ii2 = 0; ii2 < TriangleList.Count; ii2++)
{
if (TriangulatePolygonSubFunc_InCircle(ExpandedXZ[ii1], ExpandedXZ[TriangleList[ii2].p1],ExpandedXZ[TriangleList[ii2].p2],ExpandedXZ[TriangleList[ii2].p3]))
{
Edges.Add(new Edge(TriangleList[ii2].p1, TriangleList[ii2].p2));
Edges.Add(new Edge(TriangleList[ii2].p2, TriangleList[ii2].p3));
Edges.Add(new Edge(TriangleList[ii2].p3, TriangleList[ii2].p1));
TriangleList.RemoveAt(ii2);
ii2--;
}
}
if (ii1 >= VertexCount) { continue; }
//判断相同的三个点构成的三角形
for (int ii2 = Edges.Count - 2; ii2 >= 0; ii2--)
{
for (int ii3 = Edges.Count - 1; ii3 >= ii2 + 1; ii3--)
{
if (Edges[ii2].Equals(Edges[ii3]))
{
Edges.RemoveAt(ii3);
Edges.RemoveAt(ii2);
ii3--;
continue;
}
}
}
for (int ii2 = 0; ii2 < Edges.Count; ii2++)
{
TriangleList.Add(new Triangle(Edges[ii2].p1, Edges[ii2].p2, ii1));
}
Edges.Clear();
Edges = null;
}
//大于点集外围的点
for (int ii1 = TriangleList.Count - 1; ii1 >= 0; ii1--)
{
if (TriangleList[ii1].p1 >= VertexCount ||TriangleList[ii1].p2 >= VertexCount ||TriangleList[ii1].p3 >= VertexCount)
{
TriangleList.RemoveAt(ii1);
}
}
//不在房间内的面
for(int ii3 = 0;ii3<TriangleList.Count;ii3++){
if(TriangleInPolygonOuter(XZofVertices,XZofVertices[TriangleList[ii3].p1],XZofVertices[TriangleList[ii3].p2],XZofVertices[TriangleList[ii3].p3])){
TriangleList.RemoveAt(ii3);
ii3--;
}
}
TriangleList.TrimExcess();
int[] Triangles = new int[3 * TriangleList.Count];
for (int ii1 = 0; ii1 < TriangleList.Count; ii1++)
{
Triangles[3 * ii1] = TriangleList[ii1].p1;
Triangles[3 * ii1 + 1] = TriangleList[ii1].p2;
Triangles[3 * ii1 + 2] = TriangleList[ii1].p3;
}
return Triangles;
}
static bool TriangulatePolygonSubFunc_InCircle(Vector2 p, Vector2 p1, Vector2 p2, Vector2 p3) {
if (Mathf.Abs(p1.y - p2.y) < 0.0000001&&Mathf.Abs(p2.y - p3.y) < 0.0000001)
{
return false;
}
float m1, m2, mx1, mx2, my1, my2, xc, yc;
if (Mathf.Abs(p2.y - p1.y) < 0.0000001)
{
m2 = -(p3.x - p2.x) / (p3.y - p2.y);
mx2 = (p2.x + p3.x) * 0.5f;
my2 = (p2.y + p3.y) * 0.5f;
xc = (p2.x + p1.x) * 0.5f;
yc = m2 * (xc - mx2) + my2;
}
else if (Mathf.Abs(p3.y - p2.y) < 0.0000001)
{
m1 = -(p2.x - p1.x) / (p2.y - p1.y);
mx1 = (p1.x + p2.x) * 0.5f;
my1 = (p1.y + p2.y) * 0.5f;
xc = (p3.x + p2.x) * 0.5f;
yc = m1 * (xc - mx1) + my1;
}
else
{
m1 = -(p2.x - p1.x) / (p2.y - p1.y);
m2 = -(p3.x - p2.x) / (p3.y - p2.y);
mx1 = (p1.x + p2.x) * 0.5f;
mx2 = (p2.x + p3.x) * 0.5f;
my1 = (p1.y + p2.y) * 0.5f;
my2 = (p2.y + p3.y) * 0.5f;
xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);
yc = m1 * (xc - mx1) + my1;
}
float dx = p2.x - xc;
float dy = p2.y - yc;
float rsqr = dx * dx + dy * dy;
dx = p.x - xc;
dy = p.y - yc;
double drsqr = dx * dx + dy * dy;
return (drsqr <= rsqr);
}
static bool TriangleInPolygonOuter(Vector2[] pList,Vector2 p1,Vector2 p2,Vector2 p3){
Vector2[] centerPoint = new Vector2[3];
centerPoint[0] = new Vector2((p1.x+p2.x)/2,(p1.y+p2.y)/2);
centerPoint[1] = new Vector2((p1.x+p3.x)/2,(p1.y+p3.y)/2);
centerPoint[2] = new Vector2((p3.x+p2.x)/2,(p3.y+p2.y)/2);
for(int j = 0,crossNum = 0;j<centerPoint.Length;j++){
for (int i = 0; i < pList.Length; i++)
{
if (IsPointInLine(centerPoint[j].x, centerPoint[j].y, pList[i].x, pList[i].y, pList[(i+1)%pList.Length].x, pList[(i+1)%pList.Length].y)==0)
{
crossNum=crossNum+1;
continue;
}else if(IsPointInLine(centerPoint[j].x, centerPoint[j].y, pList[i].x, pList[i].y, pList[(i+1)%pList.Length].x, pList[(i+1)%pList.Length].y)==2){
crossNum = 1;
break;
}
}
if ((crossNum % 2) == 0)
{
return true;
}
crossNum = 0;
}
return false;
}
//0 在外 1 在内 2 边上
static int IsPointInLine(float x,float y,float x1,float y1,float x2,float y2)
{
float maxY =y1;
float minY = y2;
if(y1>y2){
maxY = y1;
minY = y2;
}else{
maxY = y2;
minY = y1;
}
float averageX = (x1+x2)/2;
float averageY = (y1+y2)/2;
if(y==averageY&&x==averageX){
return 2;
}
if (y < maxY && y >minY)
{
if (x >(x1 + (x2 - x1) * (y - y1) / (y2 - y1)))
{
return 0;
}
}
return 1;
}
}
struct Triangle
{
public int p1;
public int p2;
public int p3;
public Triangle(int point1, int point2, int point3)
{
p1 = point1; p2 = point2; p3 = point3;
}
}
class Edge
{
public int p1;
public int p2;
public Edge(int point1, int point2)
{
p1 = point1; p2 = point2;
}
public Edge() : this(0, 0)
{}
public bool Equals(Edge other)
{
return ((this.p1 == other.p2) && (this.p2 == other.p1)) ||((this.p1 == other.p1) && (this.p2 == other.p2));
}
}
这个类上一张已经说过了,就是画不规则图形的类,不过我这篇文章是把圆和不规则拼接出带有圆弧状的图形,看图大家就会明白了
using UnityEngine;
using System.Collections;
public class ChartletManager : System.Object {
Bezier myBezier;
public ChartletManager(){
}
public GameObject WallChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,float height,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[52];
for(int i = 0;i<52;i++){
if(i<26){
myVertices[i] = myBezier.GetPointAtTime( (float)((i) *0.04) );
myVertices[i] = new Vector3(myVertices[i].x,myVertices[i].y,myVertices[i].z-height);
}else{
myVertices[i] = myBezier.GetPointAtTime( (float)((i-26) *0.04) );
myVertices[i] = new Vector3(myVertices[i].x,myVertices[i].y,myVertices[i].z);
}
}
myMesh.vertices = myVertices;
int[] myTriangles = new int[52 * 3];
for(int i = 0; i < 52; i++){
if(i<25){
myTriangles[i*3] = 26+i;
myTriangles[i*3+1] = i;
myTriangles[i*3+2] = i+1;
}else if(i == 25||i==51){
myTriangles[i*3] = 0;
myTriangles[i*3+1] = 0;
myTriangles[i*3+2] = 0;
}else{
myTriangles[i*3+2] = i;
myTriangles[i*3+1] = i+1;
myTriangles[i*3] = i-25;
}
}
Vector2[] myuvs = new Vector2[52];
for (int i = 0; i < 52; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = myTriangles;
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
public GameObject CircleChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[27];
myVertices[0] = new Vector3(0,0,0);
for(int i =0; i <= 25; i++)
{
myVertices[i+1] = myBezier.GetPointAtTime( (float)(i *0.04) );
}
myMesh.vertices = myVertices;
Vector2[] myuvs = new Vector2[27];
for (int i = 0; i < 27; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = TriangleSubdivision.TriangulatePolygon(myuvs);
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
public GameObject CircleAndTriangleChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,Vector3[] points,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[27+points.Length];
myVertices[0] = new Vector3((startPoint.x+endPoint.x)/2,(startPoint.y+endPoint.y)/2,(startPoint.z+endPoint.z)/2);
for(int i =0; i <= 25; i++)
{
myVertices[i+1] = myBezier.GetPointAtTime( (float)(i *0.04) );
}
for(int i = 27;i<27+points.Length;i++){
myVertices[i] = points[i-27];
}
myMesh.vertices = myVertices;
Vector2[] myuvs = new Vector2[27+points.Length];
for (int i = 0; i < myuvs.Length; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = TriangleSubdivision.TriangulatePolygon(myuvs);
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
}
为了方便大家测试,我把我的测试放在了一个类里,大家直接调这个方法即可,我是测试用的,大家可以修改成自己的脚本
using UnityEngine;
public class MyBezier : MonoBehaviour
{
public Bezier myBezier;
public GameObject circleline;
public Texture2D tex;
void Start()
{
GameObject floorTexture = (GameObject)Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
GameObject wallTexture =(GameObject) Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
ChartletManager chartlet = new ChartletManager();
Vector3[] ceilVertices = new Vector3[4];
ceilVertices[0] = new Vector3(-4,0,0);
ceilVertices[1] = new Vector3(-4,-5,0);
ceilVertices[2] = new Vector3(4,-5,0);
ceilVertices[3] = new Vector3(4,0,0);
// ceilVertices[1] = new Vector3(-5,1,0);
// ceilVertices[2] = new Vector3(-5,-4,0);
// ceilVertices[3] = new Vector3(-2,-4.5f,0);
// ceilVertices[4] = new Vector3(-2.5f,-2,0);
// ceilVertices[5] = new Vector3(2,-2.5f,0);
// ceilVertices[6] = new Vector3(2.5f,-4,0);
// ceilVertices[7] = new Vector3(5,-4,0);
// ceilVertices[8] = new Vector3(5,0,0);
// ceilVertices[9] = new Vector3(4,0,0);
wallTexture= chartlet.WallChartletInMesh(wallTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),3.0f,tex,0,6);
floorTexture= chartlet.CircleAndTriangleChartletInMesh(floorTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),ceilVertices,tex,0,6);
}
}
测试用例,大家可以做自己想要的东西了,CircleAndTriangleChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,Vector3[] points
,Texture2D tex,float excursion,float zoom)
我解释一下这个类的传递参数吧
obj,就是传进来的obj对象,大家可以使用out,那个直接能用了
startPoint圆弧起始点
endPoint终点圆弧点
points 是传入的不规则图形的各个点
tex 是那张贴图
excursion这个是圆弧的 倾斜度
zoom是圆弧的大小就是圆弧顶点到起始点于终止点中间的那个点的距离 正规半圆这个值应该是圆半径的1.5倍
using UnityEngine;
public class MyBezier : MonoBehaviour
{
public Bezier myBezier;
public GameObject circleline;
public Texture2D tex;
void Start()
{
GameObject floorTexture = (GameObject)Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
GameObject wallTexture =(GameObject) Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
ChartletManager chartlet = new ChartletManager();
Vector3[] ceilVertices = new Vector3[10];
ceilVertices[0] = new Vector3(-4,0,0);
// ceilVertices[1] = new Vector3(-4,-5,0);
// ceilVertices[2] = new Vector3(4,-5,0);
// ceilVertices[3] = new Vector3(4,0,0);
ceilVertices[1] = new Vector3(-5,1,0);
ceilVertices[2] = new Vector3(-5,-4,0);
ceilVertices[3] = new Vector3(-2,-4.5f,0);
ceilVertices[4] = new Vector3(-2.5f,-2,0);
ceilVertices[5] = new Vector3(2,-2.5f,0);
ceilVertices[6] = new Vector3(2.5f,-4,0);
ceilVertices[7] = new Vector3(5,-4,0);
ceilVertices[8] = new Vector3(5,0,0);
ceilVertices[9] = new Vector3(4,0,0);
wallTexture= chartlet.WallChartletInMesh(wallTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),3.0f,tex,3,8);
floorTexture= chartlet.CircleAndTriangleChartletInMesh(floorTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),ceilVertices,tex,3,8);
}
}
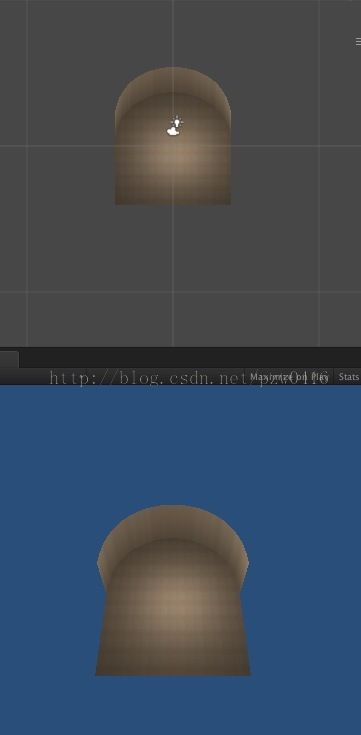
如果我数值改改就会出现这种,zoom就是倾斜程度,当然也可以是负数,是往里凹进去的,excursion是负数就向另一个方向倾斜。
凹进去的就是这种情况,具体情况大家可以测试,值的范围有限制的,超出了,会出现空的情况,当然我写的也有很多不足之处,大家可以修改修改


不知为何 csdn编辑问题,我的图片文字与代码都混合了 所以乱了 我把我的工程打包上去 大家可以下载看看具体实现效果
下载地址
http://download.csdn.net/detail/pzw0416/6727303