利用智能手机(Android)追踪一块磁铁(二)
在上一篇博客中提到了利用磁场强度推算传感器位置坐标的公式,下面就介绍怎么利用智能手机完成磁铁的追踪(任何具有磁感应器的装置均可以),这里主要是利用Android手机。
1:程序步骤:
-
首先将磁铁放置在远离手机的位置,然后拿着手机在空中做"倒8"字运动(就是这个运动轨迹:
 )。这样做的目的就是标准化手机的磁感应器,因为磁感应装置很容易受到磁场的干扰变得不精准。
)。这样做的目的就是标准化手机的磁感应器,因为磁感应装置很容易受到磁场的干扰变得不精准。
-
将手机放置平稳,然后记录当前的磁场强度,作为"原始磁场"(这个磁场必须精准可以取多次的平均值)。Android开发中需要用到SensorEventListener类。
-
然后将磁体放在距离手机20cm左右的距离,且磁铁位置在手机所在的水平线之上。之所以这么做是因为磁场强度和距离的k次幂成反比,如果太近会影响手机的磁感应器,太远磁场衰减的又太快。位于手机所在的水平线之上,是因为之前说过在xy平面上,上一篇所推的公式是不可用的。
-
记录当前的磁场作为"中心磁场", "中心磁场"减去"原始磁场"就是磁体在手机的磁感应器位置产生的磁场强度。然后根据上一篇的公式就可以计算一个"中心位置"。
-
移动磁铁,根据磁场的变化就可以实时的减去原始磁场,然后计算出磁感应器相对于磁铁的位置。然后减去"中心位置"就是得到了一个"相对于中心位置"的"移动"。
-
如图1:r1和r2的矢量位置可以通过上一篇的公式计算出来,然后r3=r1-r2就是磁铁相对于中心的移动位置,知道这个值就可以追踪磁铁的相对移动位置。
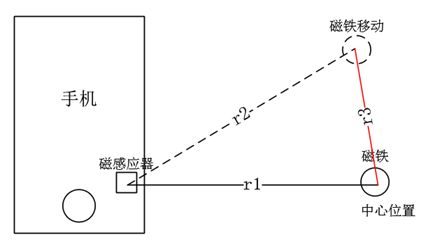
图1
2:磁场强度值的平滑滤波:
上述方法利用android进行编码后发现效果很差,主要是因为利用磁感应器得到的磁场值是不平滑的,磁场值无时无刻不在波动。造成了磁铁在定位时位置也在波动。如图2就是原始的未经过平滑过的磁场值,可以看到磁场的波动很大。图中的三个线就是磁场在xyz三个轴上产生的磁场值。

图2
因此需要对磁场值进行平滑滤波,我用的办法是卡尔曼滤波算法,有兴趣的可以去查一下资料,这里不做详细的介绍。主要介绍一下我针对本算法对卡尔曼算法做的一些改变。图3是卡尔曼的5个方程(图片中的-2应该改成-1),图4是针对方程的说明。因为这里磁场值为xyz三个轴上的分量为一维的值,所以用不到矩阵的计算,所以上述公式化简后是比较简单的(参考:http://blog.chinaunix.net/uid-26694208-id-3184442.html)。
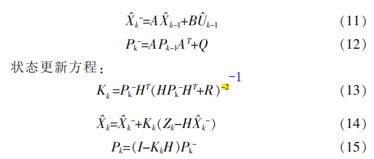
图3

图4
这里需要针对Q和R两个参数进行说明,Q:说是噪声协方差矩阵,我理解就是Q的大小决定了最优值是更接近于测量值还是估计值。R:为过程噪声协方差,我理解就是再不做任何处理的情况下测量磁场值,然后根据测量值计算方差就是R,可以通过实验得到R的值。
而Q的值这需要进行判断,假设 ,K值就决定了Q的大小。当Q越大(k越大)时卡尔曼中的最优值就越接近于测量值,而Q越小(k越小)卡尔曼中的最优值就越接近于先验估计值。通俗的讲就是Q越大平滑的效果就越不好,而平滑后的值就越"跟随"(所谓的"跟随"就是原始测量值进行快速变化时,经过平滑过的值也很好的跟着变化)。而Q越小平滑的效果就越好,而平滑后的值越"不跟随"。
,K值就决定了Q的大小。当Q越大(k越大)时卡尔曼中的最优值就越接近于测量值,而Q越小(k越小)卡尔曼中的最优值就越接近于先验估计值。通俗的讲就是Q越大平滑的效果就越不好,而平滑后的值就越"跟随"(所谓的"跟随"就是原始测量值进行快速变化时,经过平滑过的值也很好的跟着变化)。而Q越小平滑的效果就越好,而平滑后的值越"不跟随"。
举个例子,假设测量的三个值为[0,1.0,0],如果Q值很大那么平滑后的效果为[0,0.8,0]。而如果Q值很小平滑后的值为[0,0.1,0]。
所以必须找一个好的Q值做出"平滑"和"跟随"之间的平衡,在试验过程中我把k值设为-4结果平滑的效果不错,可以很好的定位磁铁的位置(第一篇博客中的演示视频中的k值就是-4)。之前说过演示视频不是最终的结果,然后我对Q值得计算做了一下设想:既然又要做到"平滑"又要做到"跟随",那么就可以根据磁场值的变化动态的确定Q的值。即当磁场变化越大时就增加Q的值使之"跟随",当磁场变化越小时就减小Q的值使之更加"平滑"。假设在卡尔曼滤波中,当前的测量值为 ,上一状态的最优值为
,上一状态的最优值为 。而两者之差的绝对值为
。而两者之差的绝对值为 ,然后假设
,然后假设 和k为
和k为 的函数
的函数 。
。
接下来就是确定函数 ,根据设想
,根据设想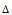 越大k就应该越大,而
越大k就应该越大,而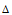 越小k越小。那么首先想到的就是线性函数
越小k越小。那么首先想到的就是线性函数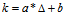 (a,b为未知数)。得出的实验效果如图5(黑色线为原始磁场,绿色为平滑后的磁场),可以看到这种方法确实可以做到即"平滑"又"跟随"。但是仔细观察图片你会发现当磁场剧烈变化到平稳的过程中,"绿色"线总是不能很快的回到平稳状态(不能很快的接近黑色线)。
(a,b为未知数)。得出的实验效果如图5(黑色线为原始磁场,绿色为平滑后的磁场),可以看到这种方法确实可以做到即"平滑"又"跟随"。但是仔细观察图片你会发现当磁场剧烈变化到平稳的过程中,"绿色"线总是不能很快的回到平稳状态(不能很快的接近黑色线)。

图5
因为 是平均映射,所以为了解决不能很快平稳的问题,需要一个"非平均映射"。即当
是平均映射,所以为了解决不能很快平稳的问题,需要一个"非平均映射"。即当 变小时需要k值变小的速度要远大于
变小时需要k值变小的速度要远大于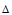 ,因此想到非平均映射函数log。因此假设
,因此想到非平均映射函数log。因此假设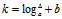 (计算a和b的值可以找两个点带入计算,比如当
(计算a和b的值可以找两个点带入计算,比如当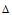 为0.1时k=-7,
为0.1时k=-7,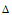 为3.0时k=-1,然后计算a和b。这两个参数就可以很好的做到"平滑"和"跟随")。然后得到实验结果如图6(黑色为原始磁场,蓝色谁平均映射,红色为非平均映射):可以看出红色线的效果明显好于蓝色线。[注:上述关于卡尔曼滤波均是本人的理解,并不能保证理论上也正确。而实验结果还不错。如果有人有更好的方法或者意见请务必和我联系E-mail:[email protected]]
为3.0时k=-1,然后计算a和b。这两个参数就可以很好的做到"平滑"和"跟随")。然后得到实验结果如图6(黑色为原始磁场,蓝色谁平均映射,红色为非平均映射):可以看出红色线的效果明显好于蓝色线。[注:上述关于卡尔曼滤波均是本人的理解,并不能保证理论上也正确。而实验结果还不错。如果有人有更好的方法或者意见请务必和我联系E-mail:[email protected]]

图6
3:注意事项:
上面的介绍就是编程需要的知识,我是在android进行实验的,在其他设备上也应该没问题。下面介绍一下需要注意的地方。
-
实验前拿着手机"画"倒8字,为了标准化磁感应器。不然不标准的吃感应器没办法进行精确测量。
-
保证磁铁在手机的上面和侧面,因为之前介绍过在xy平面上述的公式是不成立的。
-
磁铁不要距离太远和太近,太远无法检测磁场,太近会影响磁感应器。
现在关于利用智能手机(Android)追踪磁铁的内容全部介绍完了,如果有人有问题,想法,兴趣等可以联系我E-mail:[email protected]