POJ 1470 Closest Common Ancestors （LCA入门题）

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 11659		Accepted: 3848

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...

The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
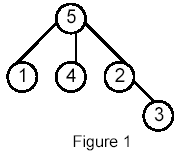
For example, for the following tree:

Sample Input

5

5:(3) 1 4 2

1:(0)

4:(0)

2:(1) 3

3:(0)

6

(1 5) (1 4) (4 2)

      (2 3)

(1 3) (4 3)

Sample Output

2:1

5:5

Hint

Huge input, scanf is recommended.

Source

Southeastern Europe 2000

 

离线算法：

/*

POJ 1470

离线处理

G++  1204ms 8788K

C++  954ms  8304K

*/



#include<stdio.h>

#include<string.h>

#include<iostream>

#include<algorithm>

#include<math.h>

#include<vector>

using namespace std;



const int MAXN=1000;

const int MAXM=500000;//最大查询数





int F[MAXN];//并查集

int r[MAXN];//并查集中集合的个数

bool vis[MAXN];//访问标记

int ancestor[MAXN];//祖先

struct Node

{

    int to,next;

}edge[MAXN*2];



int head[MAXN];

int tol;

void addedge(int a,int b)

{

    edge[tol].to=b;

    edge[tol].next=head[a];

    head[a]=tol++;

    edge[tol].to=a;

    edge[tol].next=head[b];

    head[b]=tol++;

}





struct Query

{

    int q,next;

    int index;//查询编号

}query[MAXM*2];//查询数

int answer[MAXM];//查询结果

int cnt;

int h[MAXM];

int tt;

int Q;//查询个数





void add_query(int a,int b,int i)

{

    query[tt].q=b;

    query[tt].next=h[a];

    query[tt].index=i;

    h[a]=tt++;

    query[tt].q=a;

    query[tt].next=h[b];

    query[tt].index=i;

    h[b]=tt++;

}



void init(int n)

{

    for(int i=1;i<=n;i++)

    {

        F[i]=-1;

        r[i]=1;

        vis[i]=false;

        ancestor[i]=0;

        tol=0;

        tt=0;

        cnt=0;//已经查询到的个数

    }

    memset(head,-1,sizeof(head));

    memset(h,-1,sizeof(h));

}

int find(int x)

{

    if(F[x]==-1)return x;

    return F[x]=find(F[x]);

}



void Union(int x,int y)//合并

{

    int t1=find(x);

    int t2=find(y);

    if(t1!=t2)

    {

        if(r[t1]<=r[t2])

        {

            F[t1]=t2;

            r[t2]+=r[t1];

        }

        else

        {

            F[t2]=t1;

            r[t1]+=r[t2];

        }

    }

}





void LCA(int u)

{

   // if(cnt>=Q)return;//这个不能加，加了就WR了

    ancestor[u]=u;

    vis[u]=true;//这个一定要放在前面

    for(int i=head[u];i!=-1;i=edge[i].next)

    {

        int v=edge[i].to;

        if(vis[v])continue;

        LCA(v);

        Union(u,v);

        ancestor[find(u)]=u;

    }

    for(int i=h[u];i!=-1;i=query[i].next)

    {

        int v=query[i].q;

        if(vis[v])

        {

            answer[query[i].index]=ancestor[find(v)];

            cnt++;//已经找到的答案数

        }

    }

}



int Count_num[MAXN];

bool flag[MAXN];

int main()

{

   // freopen("in.txt","r",stdin);

   // freopen("out.txt","w",stdout);

    int N;

    int u,v,m;

    char ch;

    while(scanf("%d",&N)!=EOF)

    {

        init(N);

        memset(flag,false,sizeof(flag));

        for(int i=1;i<=N;i++)

        {

            scanf("%d:(%d)",&u,&m);

            while(m--)

            {

                scanf("%d",&v);

                flag[v]=true;

                addedge(u,v);

            }

        }

        scanf("%d",&Q);

        for(int i=0;i<Q;i++)

        {

            cin>>ch;

            scanf("%d%d",&u,&v);

            cin>>ch;

            add_query(u,v,i);

        }

        int root;

        for(int i=1;i<=N;i++)

          if(!flag[i])

          {

              root=i;

              break;

          }

        LCA(root);



        memset(Count_num,0,sizeof(Count_num));

        for(int i=0;i<Q;i++)

           Count_num[answer[i]]++;

        for(int i=1;i<=N;i++)

          if(Count_num[i]>0)

            printf("%d:%d\n",i,Count_num[i]);

    }

    return 0;

}

 

 

在线算法：

/*

POJ 1470

在线处理

C++  875ms  520K

G++  1313ms  1061K

*/



#include<stdio.h>

#include<iostream>

#include<math.h>

#include<string.h>

#include<algorithm>

using namespace std;



const int MAXN=10010;



int rmq[2*MAXN];//建立RMQ的数组



//***************************

//ST算法，里面含有初始化init(n)和query(s,t)函数

//点的编号从1开始，1-n.返回最小值的下标

//***************************

struct ST

{

    int mm[2*MAXN];//mm[i]表示i的最高位，mm[1]=0,mm[2]=1,mm[3]=1,mm[4]=2

    int dp[MAXN*2][20];

    void init(int n)

    {

        mm[0]=-1;

        for(int i=1;i<=n;i++)

        {

            mm[i]=((i&(i-1))==0?mm[i-1]+1:mm[i-1]);

            dp[i][0]=i;

        }

        for(int j=1;j<=mm[n];j++)

          for(int i=1;i+(1<<j)-1<=n;i++)

             dp[i][j]=rmq[dp[i][j-1]]<rmq[dp[i+(1<<(j-1))][j-1]]?dp[i][j-1]:dp[i+(1<<(j-1))][j-1];

    }

    int query(int a,int b)//查询a到b间最小值的下标

    {

        if(a>b)swap(a,b);

        int k=mm[b-a+1];

        return rmq[dp[a][k]]<rmq[dp[b-(1<<k)+1][k]]?dp[a][k]:dp[b-(1<<k)+1][k];

    }

};



//边的结构体定义

struct Node

{

    int to,next;

};



/* ******************************************

LCA转化为RMQ的问题

MAXN为最大结点数。ST的数组 和 F，edge要设置为2*MAXN



F是欧拉序列，rmq是深度序列，P是某点在F中第一次出现的下标

*********************************************/



struct LCA2RMQ

{

    int n;//结点个数

    Node edge[2*MAXN];//树的边,因为是建无向边，所以是两倍

    int tol;//边的计数

    int head[MAXN];//头结点



    bool vis[MAXN];//访问标记

    int F[2*MAXN];//F是欧拉序列，就是DFS遍历的顺序

    int P[MAXN];//某点在F中第一次出现的位置

    int cnt;



    ST st;

    void init(int n)//n为所以点的总个数，可以从0开始，也可以从1开始

    {

        this->n=n;

        tol=0;

        memset(head,-1,sizeof(head));

    }

    void addedge(int a,int b)//加边

    {

        edge[tol].to=b;

        edge[tol].next=head[a];

        head[a]=tol++;

        edge[tol].to=a;

        edge[tol].next=head[b];

        head[b]=tol++;

    }



    int query(int a,int b)//传入两个节点，返回他们的LCA编号

    {

        return F[st.query(P[a],P[b])];

    }



    void dfs(int a,int lev)

    {

        vis[a]=true;

        ++cnt;//先加，保证F序列和rmq序列从1开始

        F[cnt]=a;//欧拉序列，编号从1开始，共2*n-1个元素

        rmq[cnt]=lev;//rmq数组是深度序列

        P[a]=cnt;

        for(int i=head[a];i!=-1;i=edge[i].next)

        {

            int v=edge[i].to;

            if(vis[v])continue;

            dfs(v,lev+1);

            ++cnt;

            F[cnt]=a;

            rmq[cnt]=lev;

        }

    }



    void solve(int root)

    {

        memset(vis,false,sizeof(vis));

        cnt=0;

        dfs(root,0);

        st.init(2*n-1);

    }

}lca;

int Count_num[MAXN];

bool flag[MAXN];

int main()

{

  //  freopen("in.txt","r",stdin);

  //  freopen("out.txt","w",stdout);

    int N;

    int u,v,m;

    char ch;

    int Q;

    while(scanf("%d",&N)!=EOF)

    {

        lca.init(N);

        memset(flag,false,sizeof(flag));

        for(int i=1;i<=N;i++)

        {

            scanf("%d:(%d)",&u,&m);

            while(m--)

            {

                scanf("%d",&v);

                flag[v]=true;

                lca.addedge(u,v);

            }

        }

        int root;

        for(int i=1;i<=N;i++)

          if(!flag[i])

          {

              root=i;

              break;

          }

        lca.solve(root);

        memset(Count_num,0,sizeof(Count_num));

        scanf("%d",&Q);

        for(int i=0;i<Q;i++)

        {

            cin>>ch;

            scanf("%d%d",&u,&v);

            cin>>ch;

            int temp=lca.query(u,v);

            Count_num[temp]++;

        }

        for(int i=1;i<=N;i++)

          if(Count_num[i]>0)

            printf("%d:%d\n",i,Count_num[i]);

    }

    return 0;

}