【人工智能】蚁群算法(密恐勿入)
蚁群算法(密恐勿入)
蚁群算法--给你一个感性认识
- 蚁群算法(密恐勿入)
-
- 1. 算法简介
-
- 1.1 基本原理
- 1.1.1 模拟蚂蚁在简单地形,寻找食物
- 1.1.2 模拟蚂蚁在复杂地形,找到食物
- 1.2 算法应用
- 2. 算法解析
- 3.算法应用——TSP问题
-
- 3.1 TSP旅行商介绍
- 3.2 利用蚁群算法解决TSP问题
- 总结一下:
- 4. TSP问题—蚁群算法实现(python版本)
-
- 问题背景:
- 数据:
- 准备阶段
- 算法构造
- 测试:
1. 算法简介
1.1 基本原理
蚁群算法是一种模拟蚂蚁觅食行为的启发式算法,被广泛应用于优化问题的求解。蚁群算法的基本思想是,将一群蚂蚁放在问题的解空间上,让它们通过信息素的传递和挥发,逐渐找到最优解。
1.1.1 模拟蚂蚁在简单地形,寻找食物
阶段一:在蚁群算法的初始阶段,我们在地图上不放置任何食物,因为蚂蚁需要在没有任何信息素的情况下开始摸索前进。一开始,蚂蚁们在洞外随机移动,试图找到食物的位置。每只蚂蚁的速度相同,它们会按照随机的方向前进,直到遇到障碍物或者到达了边界。此时,它们会再次随机选择一个方向,并继续前进。这个过程会持续进行,
阶段二:当蚂蚁们找到了食物后,它们会将一些信息素沿着它们的路径释放出来,并且在回到蚁巢的路上也会释放信息素。
蚁群之间的规则:
- 蚂蚁发现食物并将其带回巢穴时,通常会遵循已经标记的路径返回,即原路返回。在返回过程中,蚂蚁会释放归巢素和信息素,这些化学物质可以吸引其他蚂蚁跟随它的路径前往食物源。如果路径上有较多的归巢素或信息素,则越来越多的蚂蚁将会选择这条路径前往食物。
阶段三:当蚂蚁们回到巢穴时,它们会在原来的路径上释放更多信息素,增强这条路径的吸引力,并且尝试着寻找更短的路径。蚂蚁们会在路径上选择合适的地方停下来,释放信息素,然后返回巢穴。这个过程将持续进行,直到蚂蚁们找到了最优路径。
根据以上规则,随着时间的推移,蚂蚁们终会(可能)找到的最优路径。

1.1.2 模拟蚂蚁在复杂地形,找到食物
1.2 算法应用
蚁群算法已经应用于多种优化问题的求解,比如:
- 旅行商问题
- 图着色问题
- 网络路由问题
- 调度问题
- 生产计划问题
在这些问题中,蚁群算法通常能够找到较优的解。此外,蚁群算法还可以用于机器学习领域中的聚类和分类等问题。
2. 算法解析
想要理解算法?需要去理解以下内容:
- 蚁群是如何找到解的?解的步骤是什么?
- 蚂蚁在初始时随机选择一个起点,并向前行走。
- 当蚂蚁走到一个节点时,它会选择一个下一个节点进行移动。蚂蚁选择下一个节点的概率与该节点上的信息素浓度成正比。信息素浓度越高的节点,被选择的概率也越高。
- 当蚂蚁移动到一个节点时,它会在该节点上释放一定量的信息素。
- 当蚂蚁找到解后,它会回到起点,并在路径上释放更多的信息素,增强这条路径的吸引力。
- 当其他蚂蚁在寻找解的过程中遇到已经被标记的路径时,它们会更有可能选择这条路径。
- 随着时间的推移,信息素会挥发,路径上信息素的浓度会逐渐降低。这样,路径上的信息素浓度会经历一个上升和下降的过程。
- 蚂蚁们会根据路径上的信息素浓度来选择下一个节点。当信息素浓度很高时,它们更有可能选择这条路径。
- 蚂蚁们持续寻找解,直到找到最优解或者达到预设的迭代次数。
蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标的。我们举例简单说明蚂蚁觅食行为:

现阶段 蚂蚁有A→B→C 和 A→D→C两种较优路径, A→D→C的距离要大于A→B→C
因为大量蚂蚁的选择概率会不一样,会将蚂蚁大致分为两批,一批走A→B→C ,另一批走A→D→C,单位时间内A→B→C通过蚂蚁也要大于 A→D→C,随着时间的推移,A→B→C的信息素越来越多,正反馈调节下,走此条路径的蚂蚁也越来越多。所以越短路径的浓度会越来越大,经过此短路径达到目的地的蚂蚁也会比其他路径多。这样大量的蚂蚁实践之后就找到了最短路径。所以这个过程本质可以概括为以下几点:
- 路径概率选择机制信息素踪迹越浓的路径,被选中的概率越大
- 信息素更新机制路径越短,路径上的信息素踪迹增长得越快
- 协同工作机制蚂蚁个体通过信息素进行信息交流。
蚂蚁在蚁群算法中通过信息素的传递和挥发来进行交流。通过信息素的传递和挥发,整个蚁群就会产生信息正反馈现象、种群分化等。
-
正反馈现象
由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越大。
在一个人流量比较大的商场,人们往往会选择人流量比较大的走廊或者通道来走,因为人流量越大,越能够说明这个通道是正确的,这样就会产生一种信息正反馈现象,后来的人也会选择这条路线,进一步增加这条路线的人流量。与蚁群算法类似,人们会根据前人的经验来选择路线,从而产生类似的正反馈现象。
-
种群分化
种群分化是蚁群算法中的一个现象,当蚂蚁在搜索过程中遇到了局部最优解时,会一直围绕这个局部最优解寻找,并且释放信息素。这会导致其他蚂蚁也会被吸引过来,导致整个蚁群陷入局部最优解,而无法找到全局最优解的情况。这种现象在蚁群算法中是非常常见的,需要特别注意。为了避免种群分化,蚂蚁需要具有一定的随机性,同时需要及时更新信息素,以便发现全局最优解。
一个人在某个领域上有很高的专业技能,但是如果他过于专注于这个领域,就可能会失去对其他领域的了解和认识,进而导致对问题的认识出现偏差,甚至无法解决某些问题。
就比如图1. 我如果此刻将原有阻碍去掉一部分,此时只靠信息素交流的蚁群会产生种群分化现象。陷入了局部最有解。
当蚁群算法陷入局部最优解时,可以使用以下方法进行优化:
- 增加蚂蚁的数量。增加蚂蚁的数量可以增加搜索的广度,从而有更大的可能性找到全局最优解。
- 调整信息素挥发速度。通过适当降低信息素挥发速度,可以增加信息素在路径上的积累,从而增加蚂蚁选择该路径的概率。
- 引入随机因素。在蚁群算法中引入随机因素,可以使蚂蚁更具有探索性,从而有可能跳出局部最优解,进而找到全局最优解。
- 改变参数。通过改变蚁群算法中的参数,如信息素浓度、信息素挥发速度、启发式因子等,可以使算法更加灵活,从而更容易找到全局最优解。
- 使用局部搜索算法。在蚁群算法的基础上,可以结合局部搜索算法,如模拟退火算法、遗传算法等,来寻找全局最优解。
上述的情况,可以利用第三条和第四条解决。
3.算法应用——TSP问题
3.1 TSP旅行商介绍
首先,我们先回顾一下,什么是TSP旅行商问题:
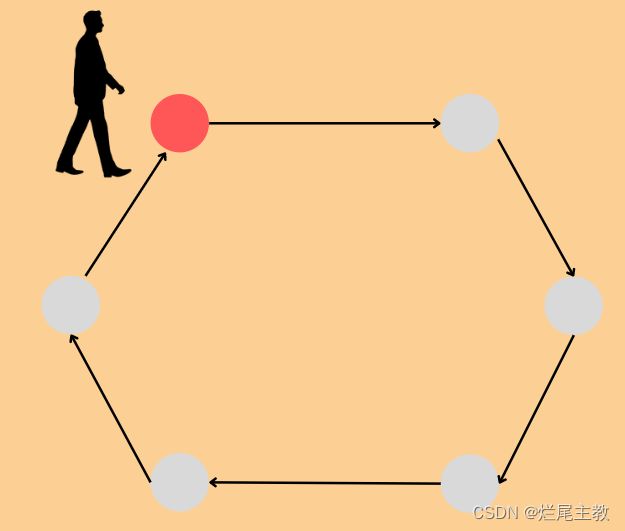
假设有一位邮递员,他从初始城市(任意一城市)出发,途径所有城市并回到初始城市,那么他一共会有
( n − 1 ) ! (n-1)! (n−1)!
条路径。从中找出那条最短路径,这就是TSP旅行商问题。
如果我们遍历的去找那个最短路径,那么随着城市的增加,计算量大大增加。

3.2 利用蚁群算法解决TSP问题
在这里,蚂蚁仅有信息素这一项能力是不够的。所以我们给与蚂蚁一些其他的能力
- 蚂蚁在一次旅行中不会重复访问相同的城市
- 蚂蚁可以知晓城市之间的距离。
- 蚂蚁在路上会释放信息素
- 蚂蚁在选择下一个城市的概率依靠以下公式:
p i j k = ( τ i j α ) ( η i j β ) ∑ allowed k ( τ i j α ) ( η i j β ) p_{i j}^{k}=\frac{\left(\tau_{i j}^{\alpha}\right)\left(\eta_{i j}^{\beta}\right)}{\sum_{\text {allowed}_k}\left(\tau_{i j}^{\alpha}\right)\left(\eta_{i j}^{\beta}\right)} pijk=∑allowedk(τijα)(ηijβ)(τijα)(ηijβ)
| 参数名称 | 参数意义 | 参数设置过大 | 参数设置过小 |
|---|---|---|---|
| 信息素因子ɑ | 反映了蚂蚁运动过程中路径上积累的信息素的量在指导蚁群搜索中的相对重要程度。取值范围通常在[1, 4]之间。 | 蚂蚁选择以前已经走过的路可能性较大,容易使随机搜索性减弱 | 蚁群易陷入纯粹的随机搜索,使种群陷入局部最优 |
| 启发函数因子 | 反映了启发式信息在指导蚁群搜索中的相对重要程度,蚁群寻优过程中先验性、确定性因素作用的强度取值范围在[0, 5]之间 | 虽然收敛速度加快,但是易陷入局部最优 | 蚁群易陷入纯粹的随机搜索,很难找到最优解 |

其实这个公式也很好理解,蚂蚁选择城市的概率主要由 τ i j ( t ) \tau_{ij}(t) τij(t)和 η i j ( ) \eta_{ij}() ηij(t)有关,分母为蚂蚁k可能访问的城市之和(为常数),这样才能使蚂蚁选择各个城市的概率之后为1,符合概率的定义。 τ i j ( t ) \tau_{ij}(t) τij(t)和$\eta_{ij}()上的指数信息素因子ɑ和启发函数因子只决定了信息素浓度以及启发函数对蚂蚁k从i到j的可能性的贡献程度。
例:下图为计算蚂蚁从起点城市2到可达城市的概率(套公式,很好理解):

图2. 此图和此节部分内容借鉴于秃头小苏:蚁群算法(实例帮助理解)
OK,蚂蚁有了这些能力后,我们只需要控制一下流程,就可以解决TSP问题了,下面是给出了此问题的一种常用的解决流程
蚁群算法解决TSP问题的算法流程
- 初始化信息素浓度矩阵 τ i j ( t ) \tau_{ij}(t) τij(t),启发式函数 η i j \eta_{ij} ηij,以及蚂蚁的位置。
- 每只蚂蚁按照信息素和启发式函数的概率选择下一个城市。
- 记录蚂蚁的路径和距离。
- 在所有蚂蚁走完所有城市之后,根据蚂蚁走过的路径和距离更新信息素浓度矩阵 η i j ( t ) \eta_{ij}(t) ηij(t)。
- 如果未达到停止条件,则返回步骤2。
其中,停止条件可以是迭代次数达到预设值或者最佳解不再改变。
起点的选择对最短路径是有影响的。不同的起点可能会导致不同的最短路径。在蚁群算法中,通过随机选择起始点,可以增加搜索的广度,从而有更大的可能性找到全局最优解。
信息素更新的时机一般有两种方式:
- 在每个迭代周期结束后进行更新,即在所有蚂蚁完成当前迭代周期后,根据其路径长度和信息素更新信息素浓度。
- 在每只蚂蚁走遍所有城市之后,立即更新信息素浓度。
信息素更新公式:
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 m Δ τ i j k ( t ) \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\sum_{k=1}^{m} \Delta \tau_{i j}^{k}(t) τij(t+1)=(1−ρ)τij(t)+k=1∑mΔτijk(t)
其中, ρ \rho ρ 是信息素挥发速度, Δ τ i j k ( t ) \Delta \tau_{i j}^{k}(t) Δτijk(t) 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,m 是蚂蚁的数量。
在每个迭代周期结束后进行更新或在每只蚂蚁走遍所有城市之后立即更新信息素浓度均可。
Delta tau 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,不同的 Delta tau 规则有以下几种:
- 静态规则:所有蚂蚁在搜索过程中释放的信息素量是相等的,即 Δ τ i j k ( t ) = Q / L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t) Δτijk(t)=Q/Lk(t),其中 Q 是常量,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 动态规则:蚂蚁在搜索过程中释放的信息素量是动态变化的,即 Δ τ i j k ( t ) = Q / L k ( t ) + ∑ k = 1 m w k ⋅ L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t)+\sum_{k=1}^{m} w_{k} \cdot L_{k}(t) Δτijk(t)=Q/Lk(t)+∑k=1mwk⋅Lk(t),其中 ∑ k = 1 m w k = 1 \sum_{k=1}^{m} w_{k}=1 ∑k=1mwk=1,w_k 是蚂蚁 k 对信息素的贡献系数,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 最大值规则:每只蚂蚁在搜索过程中释放的信息素量最多为 Δ τ i j k ( t ) = Q L b e s t \Delta \tau_{i j}^{k}(t)=\frac{Q}{L_{best}} Δτijk(t)=LbestQ,其中 L_best 是迄今为止找到的最短路径长度。
以上规则中,静态规则是最简单的,但是可能会导致信息素的浓度过高或过低,从而影响搜索效果。动态规则可以根据搜索的进展情况动态调整信息素的浓度,适应性更强。最大值规则可以防止信息素浓度过高,但可能会导致搜索无法跳出局部最优解。
例(静态规则):下图为信息素的更新过程,假设初始时各路径信息素浓度为10。

总结一下:
蚁群算法流程:
- 初始化信息素浓度矩阵_{ij}(t),启发式函数_{ij},以及蚂蚁的位置。
- 每只蚂蚁按照信息素和启发式函数的概率选择下一个城市。
- 记录蚂蚁的路径和距离。
- 在所有蚂蚁走完所有城市之后,根据蚂蚁走过的路径和距离更新信息素浓度矩阵_{ij}(t)。
- 如果未达到停止条件,则返回步骤2。
其中,停止条件可以是迭代次数达到预设值或者最佳解不再改变。
起点的选择对最短路径是有影响的。不同的起点可能会导致不同的最短路径。在蚁群算法中,通过随机选择起始点,可以增加搜索的广度,从而有更大的可能性找到全局最优解。
信息素更新的时机一般有两种方式:
- 在每个迭代周期结束后进行更新,即在所有蚂蚁完成当前迭代周期后,根据其路径长度和信息素更新信息素浓度。
- 在每只蚂蚁走遍所有城市之后,立即更新信息素浓度。
信息素更新公式:
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 m Δ τ i j k ( t ) \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\sum_{k=1}^{m} \Delta \tau_{i j}^{k}(t) τij(t+1)=(1−ρ)τij(t)+k=1∑mΔτijk(t)
其中, ρ \rho ρ 是信息素挥发速度, Δ τ i j k ( t ) \Delta \tau_{i j}^{k}(t) Δτijk(t) 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,m 是蚂蚁的数量。
在每个迭代周期结束后进行更新或在每只蚂蚁走遍所有城市之后立即更新信息素浓度均可。
Delta tau 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,不同的 Delta tau 规则有以下几种:
- 静态规则:所有蚂蚁在搜索过程中释放的信息素量是相等的,即 Δ τ i j k ( t ) = Q / L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t) Δτijk(t)=Q/Lk(t),其中 Q 是常量,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 动态规则:蚂蚁在搜索过程中释放的信息素量是动态变化的,即 Δ τ i j k ( t ) = Q / L k ( t ) + ∑ k = 1 m w k ⋅ L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t)+\sum_{k=1}^{m} w_{k} \cdot L_{k}(t) Δτijk(t)=Q/Lk(t)+∑k=1mwk⋅Lk(t),其中 ∑ k = 1 m w k = 1 \sum_{k=1}^{m} w_{k}=1 ∑k=1mwk=1,w_k 是蚂蚁 k 对信息素的贡献系数,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 最大值规则:每只蚂蚁在搜索过程中释放的信息素量最多为 Δ τ i j k ( t ) = Q L b e s t \Delta \tau_{i j}^{k}(t)=\frac{Q}{L_{best}} Δτijk(t)=LbestQ,其中 L_best 是迄今为止找到的最短路径长度。
4. TSP问题—蚁群算法实现(python版本)
问题背景:
假设有一位邮递员,他从初始城市(任意一城市)出发,途径所有城市并回到初始城市,利用蚁群算法求得最短路径
数据:
以下是10个城市的坐标数据:
| 城市 | X坐标 | Y坐标 |
|---|---|---|
| A | 5 | 10 |
| B | 6 | 15 |
| C | 10 | 15 |
| D | 14 | 14 |
| E | 20 | 10 |
| F | 16 | 5 |
| G | 8 | 5 |
| H | 4 | 8 |
| I | 8 | 12 |
| J | 12 | 12 |
准备阶段
- 首先,将数据存储在Graph中,并且计算各个城市之间的距离distances。
class Graph(object):
def __init__(self, city_location, pheromone=1.0, alpha=1.0, beta=1.0):
self.city_location = city_location
self.n = len(city_location)
# phernmone矩阵
self.pheromone = [[pheromone for _ in range(self.n)] for _ in range(self.n)]
self.alpha = alpha
self.beta = beta
# 城市之间的距离矩阵
self.distances = self._generate_distances()
# 欧式距离作为图的权重
def _generate_distances(self):
distances = []
# 遍历行
# 遍历列
# 如果行值=列,比如(1,1)(2,2),这样就是相同的城市,则距离为零
# 如果行值<列,比如(1,2)(2,3),这样就是不同的城市,距离按欧拉距离公式来算
# 否则,将矩阵的斜对称位置上的距离来补(原因:城市之间距离矩阵是一个distances[i][j] = distances[j][i]特点的矩阵,这样的目的就是减少至少一半的计算)
for index_i, _i in enumerate(self.city_location):
row = []
for index_j, _j in enumerate(self.city_location):
if _i == _j:
row.append(0)
elif _i < _j:
x1, y1 = self.city_location[str(_i)]
x2, y2 = self.city_location[str(_j)]
row.append(np.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2))
else:
row.append(distances[index_j][index_i])
distances.append(row)
return distances
- 属性
city_location: 城市位置的字典n: 城市的数量pheromone: 蚂蚁留下的信息素的矩阵alpha: 信息素强度的影响因子beta: 启发式因子的影响因子distances: 城市之间距离的矩阵
- 方法
__init__(self, city_location, pheromone=1.0, alpha=1.0, beta=1.0): 对象初始化,计算出城市之间的距离矩阵_generate_distances(self): 计算城市之间的距离矩阵
-
那么,我们将各项能力赋予蚂蚁
class Ant(object): def __init__(self, graph, start_city): self.graph = graph self.start_city = start_city self.curr_city = start_city self.visited = [False for _ in range(graph.n)] self.visited[start_city] = True self.tour_length = 0 self.tour = [start_city] def choose_next_city(self): # calculate probabilities of all cities probs = [] total_prob = 0 for i in range(self.graph.n): if not self.visited[i]: prob = self.graph.pheromone[self.curr_city][i] ** self.graph.alpha * \\ (1.0 / self.graph.distances[self.curr_city][i]) ** self.graph.beta probs.append((i, prob)) total_prob += prob # select the next city randomly based on the probabilities r = random.uniform(0, total_prob) upto = 0 for i, prob in probs: if upto + prob >= r: self.curr_city = i self.visited[i] = True self.tour.append(i) self.tour_length += self.graph.distances[self.tour[-2]][i] return upto += prob def tour_complete(self): return len(self.tour) == self.graph.n- 属性:
graph: 图对象,表示要在其上运行蚁群算法的图start_city: 整数,表示蚂蚁的起始城市curr_city: 整数,表示蚂蚁当前所在城市visited: 布尔列表,表示城市是否已被访问tour_length: 浮点数,表示蚂蚁的路径长度tour: 整数列表,表示蚂蚁的路径
- 方法:
choose_next_city(): 计算所有城市的概率,根据概率随机选择下一个城市tour_complete(): 检查蚂蚁是否已经遍历完所有城市
- 属性:
算法构造
通过上面的准备,我们现阶段有了蚂蚁和城市图,那么,我们来规划一下算法的流程。把:
- 初始化蚂蚁和信息素矩阵。
- 蚂蚁根据信息素浓度和启发函数选择下一个节点。
- 蚂蚁在路径上释放信息素。
- 重复步骤2和3,直到所有蚂蚁都找到了解。
- 评估每条路径的适应度,并更新信息素矩阵。
- 重复步骤2到5,直到达到预设的迭代次数或者找到最优解。
这里要考虑选择哪一种更新策略、更新时机:
- 静态规则(这里我选的这个)
- 在每个迭代周期结束后进行更新,即在所有蚂蚁完成当前迭代周期后,根据其路径长度和信息素更新信息素浓度。
def ant_colony(graph, num_ants, num_iterations, evaporation_rate=0.5, q=500):
shortest_tour = None # 最短路径
shortest_tour_length = float('inf') # 最短路径长度
for i in range(num_iterations):
ants = [Ant(graph, random.randint(0, graph.n - 1)) for _ in range(num_ants)] # 随机生成蚂蚁
for ant in ants:
while not ant.tour_complete():
ant.choose_next_city() # 选择下一个城市
ant.tour_length += graph.distances[ant.tour[-1]][ant.start_city] # 计算路径长度
if ant.tour_length < shortest_tour_length:
shortest_tour_length = ant.tour_length
shortest_tour = ant.tour[:]
for i in range(graph.n):
for j in range(graph.n):
if i != j:
graph.pheromone[i][j] *= (1 - evaporation_rate) # 更新挥发信息素
for ant in ants:
if (i, j) in zip(ant.tour, ant.tour[1:]):
graph.pheromone[i][j] += q / ant.tour_length # 更新释放信息素
return shortest_tour, shortest_tour_length
- 注释:
- shortest_tour:最短路径,初始化为 None。
- shortest_tour_length:最短路径长度,初始化为正无穷。
- ants:蚂蚁集合,随机生成。
- ant:蚂蚁,从 graph 中随机选择一个起始城市开始走。
- choose_next_city:选择下一个城市。
- tour_length:路径长度,初始化为 0。
- pheromone:信息素。
- evaporation_rate:信息素挥发率。
- q:信息素强度。
- zip(ant.tour, ant.tour[1:]):将 ant.tour 中的相邻两个元素组成一个二元组 (i, j),便于后续计算。
- 更新信息素时,需要更新挥发信息素和释放信息素。挥发信息素是指信息素随时间的推移而逐渐消失;释放信息素是指蚂蚁在路径上释放信息素,增强这条路径的吸引力。
- 返回最短路径和最短路径长度。
测试:
将数据和流程带入:
city_location = {
'A': (5, 10),
'B': (6, 15),
'C': (10, 15),
'D': (14, 14),
'E': (20, 10),
'F': (16, 5),
'G': (8, 5),
'H': (4, 8),
'I': (8, 12),
'J': (12, 12)
}
# 创建Graph对象
g = Graph(city_location)
shortest_tour, shortest_tour_length = ant_colony(graph=g, num_ants=500, num_iterations=1000)
print(shortest_tour,shortest_tour_length)
# 城市索引
city_index = {city: i for i, city in enumerate(sorted(city_location))}
# 城市索引
city_index = {city: i for i, city in enumerate(sorted(city_location))}
# 城市名称列表
shortest_tour = [list(city_index.keys())[i] for i in shortest_tour]
# 打印结果
print(shortest_tour)
g.plot_path(shortest_tour)
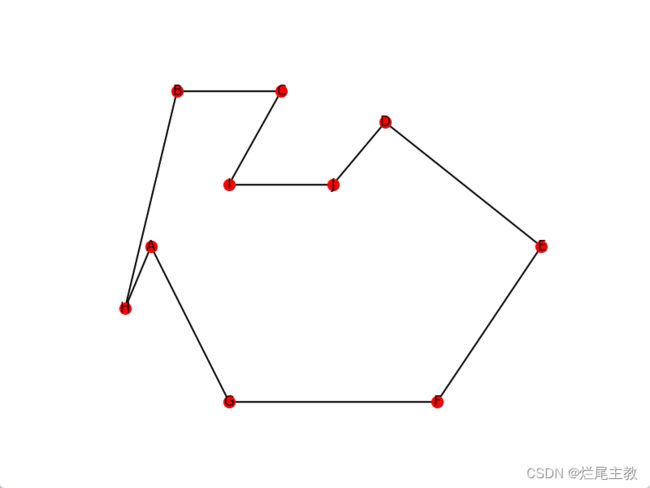
参考代码:
import math
import random
class Graph(object):
def __init__(self, n, pheromone=1.0, alpha=1.0, beta=1.0):
self.n = n
self.pheromone = [[pheromone for _ in range(n)] for _ in range(n)]
self.alpha = alpha
self.beta = beta
self.distances = self._generate_distances()
def _generate_distances(self):
# randomly generate distances between cities
distances = []
for i in range(self.n):
row = []
for j in range(self.n):
if i == j:
row.append(0)
elif j > i:
row.append(random.uniform(1, 10))
else:
row.append(distances[j][i])
distances.append(row)
return distances
class Ant(object):
def __init__(self, graph, start_city):
self.graph = graph
self.start_city = start_city
self.curr_city = start_city
self.visited = [False for _ in range(graph.n)]
self.visited[start_city] = True
self.tour_length = 0
self.tour = [start_city]
def choose_next_city(self):
# calculate probabilities of all cities
probs = []
total_prob = 0
for i in range(self.graph.n):
if not self.visited[i]:
prob = self.graph.pheromone[self.curr_city][i] ** self.graph.alpha * \\
(1.0 / self.graph.distances[self.curr_city][i]) ** self.graph.beta
probs.append((i, prob))
total_prob += prob
# select the next city randomly based on the probabilities
r = random.uniform(0, total_prob)
upto = 0
for i, prob in probs:
if upto + prob >= r:
self.curr_city = i
self.visited[i] = True
self.tour.append(i)
self.tour_length += self.graph.distances[self.tour[-2]][i]
return
upto += prob
def tour_complete(self):
return len(self.tour) == self.graph.n
def ant_colony(graph, num_ants, num_iterations, evaporation_rate=0.5, q=500):
shortest_tour = None
shortest_tour_length = float('inf')
for i in range(num_iterations):
# initialize ants
ants = [Ant(graph, random.randint(0, graph.n-1)) for _ in range(num_ants)]
# have each ant choose a path
for ant in ants:
while not ant.tour_complete():
ant.choose_next_city()
ant.tour_length += graph.distances[ant.tour[-1]][ant.start_city]
# check if this ant found a shorter tour
if ant.tour_length < shortest_tour_length:
shortest_tour_length = ant.tour_length
shortest_tour = ant.tour[:]
# update pheromones
for i in range(graph.n):
for j in range(graph.n):
if i != j:
graph.pheromone[i][j] *= (1 - evaporation_rate)
for ant in ants:
if (i, j) in zip(ant.tour, ant.tour[1:]):
graph.pheromone[i][j] += q / ant.tour_length
return shortest_tour, shortest_tour_length
# generate a 11-city TSP problem and solve it using the ant colony algorithm
graph = Graph(11)
shortest_tour, shortest_tour_length = ant_colony(graph, num_ants=10, num_iterations=50)
# print the shortest tour and its length
print("Shortest tour:", shortest_tour)
print("Shortest tour length:", shortest_tour_length)
写在最后,第二次上热门,流量还可以,我也是认真对待了这篇文章,写这篇博客的原因就是顺便把老师的作业也写了,作业你们也看到了,就是用代码实现蚁群算法去解决TSP问题,对于蚁群算法,我也是第一次去学习,并不是你们所认识的“佬”,说是博客,其实更像一篇记录我学习过程的日记,对于人工智能,说实话,挺有意思的,但考虑到本身实力情况,只能当作暂时的兴趣,大概这门课结课的时候,人工智能系列估计就不更了,唉毕竟是兴趣,不能吃饭,我的实力也不可能达到那些“佬”级别,下一篇估计也快了,应该是神经网络(泛泛而谈),有像了解的可以期待一下,我尽量把正确的,易懂的,可能老师考虑不到的方面给你们讲清楚,现学现卖的优势就是能将难点给它点出来。