力扣刷题19天
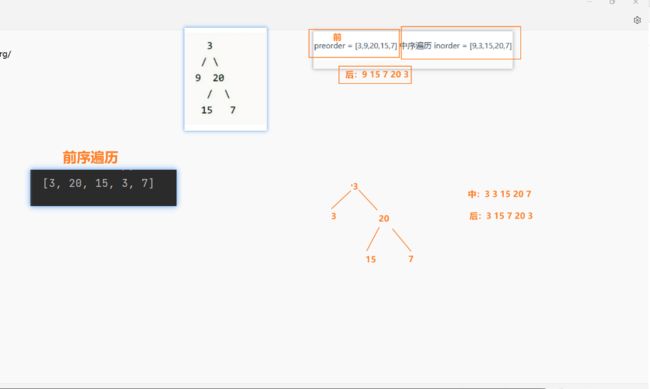
106.从中序与后序遍历序列构造二又树(1、在中序、前序和后序,每轮取得时候数量都一样. 2、必须要有中序才能推测出来)
这道题下面是前提:
运行代码:
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not postorder:
return
post_value=postorder[-1]
root=TreeNode(post_value)
index=inorder.index(post_value)
left_value=inorder[:index]
right_value=inorder[index+1:]
post_left_value=postorder[:len(left_value)]
post_right_value=postorder[len(left_value):len(left_value)+len(right_value)]#和下面的都可以
#post_right_value = postorder[len(left_value):len(postorder)-1]
root.left=self.buildTree(left_value,post_left_value)
root.right=self.buildTree(right_value,post_right_value)
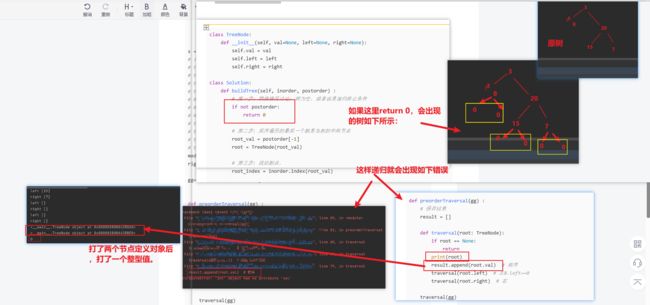
return root下面代码中出现的问题:
class TreeNode:
def __init__(self, val=None, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, inorder, postorder) :
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not postorder:
return 0
# 第二步: 后序遍历的最后一个就是当前的中间节点
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
root_index = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
left_inorder = inorder[:root_index]
right_inorder = inorder[root_index + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
left_postorder = postorder[:len(left_inorder)]
print("left",left_postorder)
right_postorder = postorder[len(left_inorder): len(postorder) - 1]
print("right", right_postorder)
# print(root.val)
# 第六步: 递归
root.left = self.buildTree(left_inorder, left_postorder)
root.right = self.buildTree(right_inorder, right_postorder)
# 第七步: 返回答案
return root
s = Solution()
# 构造一个二叉树,此处省略了构造函数的实现
# tree = TreeNode()
# targetSum=22
# tree = TreeNode(3)
# tree.left = TreeNode(3)
# # tree.left.left= TreeNode(20)
# # tree.left.left.left= TreeNode(7)
# # tree.left.left.right= TreeNode(2)
# tree.right = TreeNode(20)
# tree.right.left = TreeNode(15)
# tree.right.right = TreeNode(7)
# tree.right.right.right = TreeNode(1)
medium=[8,3,15,20,7]
right=[8,15,7,20,3]
gg=s.buildTree(medium, right)
def preorderTraversal(gg) :
# 保存结果
result = []
def traversal(root: TreeNode):
if root == None:
return
print(root)
result.append(root.val) # 前序
traversal(root.left) # 左8.left==0
traversal(root.right) # 右
traversal(gg)
return result
print(preorderTraversal(gg))
# print(s.hasPathSum(tree, targetSum)) #
105、从前序与中序遍历序列构造二叉树
和上面那道题逻辑一样。
运行代码:
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder:
return
value=preorder[0]
root=TreeNode(value)
root_index=inorder.index(value)
left_list=inorder[:root_index]#左中序
right_list=inorder[root_index+1:]#右中序
left_froat=preorder[1:len(left_list)+1]
right_froat=preorder[len(left_froat)+1:]
root.left=self.buildTree(left_froat,left_list)
root.right=self.buildTree(right_froat,right_list)
return root做题的时候存在着以下问题(在中序、前序和后序,每轮取得时候数量都一样):
654.最大二叉树
运行代码:
class Solution:
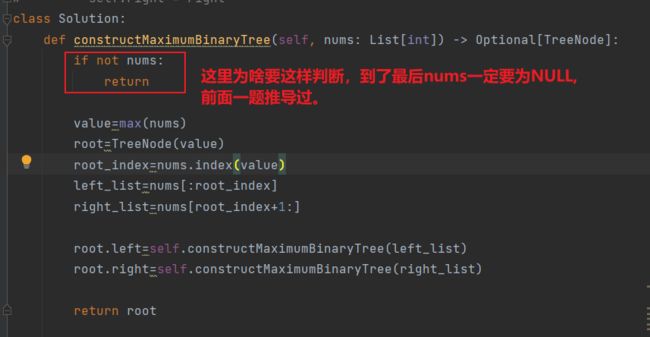
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return
value=max(nums)
root=TreeNode(value)
root_index=nums.index(value)
left_list=nums[:root_index]
right_list=nums[root_index+1:]
root.left=self.constructMaximumBinaryTree(left_list)
root.right=self.constructMaximumBinaryTree(right_list)
return root
写代码时存在问题如下:
617.合并二叉树
代码如下:
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if root1==None:
return root2#return 只是为了不往下运行
if not root2:
return root1
root1.val+=root2.val
root1.left=self.mergeTrees(root1.left,root2.left)
root1.right=self.mergeTrees(root1.right,root2.right)
return root1没啥好说的,迭代接收节点对象。
700.二叉搜索树中的搜索
前置知识:
二叉搜索树(BST)定义:
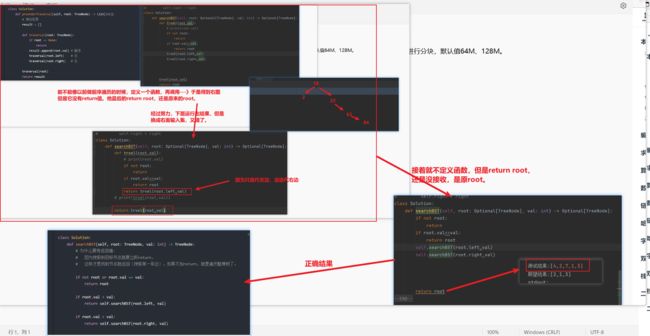
做错的思路血缘总结:
思路流程:
运行代码:
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
# 为什么要有返回值:
# 因为搜索到目标节点就要立即return,
# 这样才是找到节点就返回(搜索某一条边),如果不加return,就是遍历整棵树了。
if not root or root.val == val:
return root
if root.val > val:
return self.searchBST(root.left, val)
if root.val < val:
return self.searchBST(root.right, val)