0803平面及其方程-向量代数与空间解析几何

1 曲面方程与空间曲线方程的概念

1.1 曲面方程

如果曲面与三元方程

​ $F(x,y,z)=0$

有下述关系

（1）曲面S上的任意一点坐标满足方程

（2）不在曲面上的点都不满足方程

方程叫做曲面的方程，而曲面S就叫做方程的图形。

1.2 空间曲线的方程

空间曲线可以看做两个曲面的$S_1,S_2$的交线，设

​ $F(x,y,z)=0和G(x,y,z)=0$

分别是两个曲面的方程，则方程组
$$\{\begin{array}{l}F(x,y,z)=0\\ G(x,y,z)=0\end{array}$$
满足：

（1）在曲线C上的任意一点坐标都满足上述方程组；

（2）不在曲线上的点的坐标不满足上述方程组。

方程组叫做空间曲线C的方程，空间曲线C叫做方程组的图形。

2 平面的点法式方程

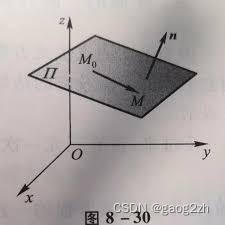
如果一非零向量垂直于一平面，这向量叫做该平面的法线向量。

如上图所示，平面上一点$M_0(x_0,y_0,z_0),它的一个法线向量n(A,B,C)$.设$M(x,y,z)$为平面上任一点，则
$$\begin{gathered} M_{0}M\perp n \\ 即M_{0}M\cdot n=0 \\ A(x-x_0)+B(y-y_0)+C(z-z_0)=0(3-3) \end{gathered}$$

• 注：在平面上的点满足方程（3-3）；不在平面上的点不满足方程（3-3）。

方程（3-3）叫做平面的点法式方程。

例1 求过点$(2,-3,0)且以n=(1,-2,3)$为法线向量的平面方程。
$$\begin{gathered} 解：带入点法式方程，得 \\ (x-2)-2(y+3)+3z=0 \\ 即x-2y+3z-8=0 \end{gathered}$$
例2 求过三点$M_1(2,-1,4),M_2(-1,3,-2)和M_3(0,2,3)$的平面方程。
解：设平面的法线向量 n ⃗ , 则 n ⃗ ⊥ M 1 M 2 ⃗ , 且 n ⃗ ⊥ M 1 M 3 ⃗ M 1 M 2 ⃗ = ( − 3 , 4 , − 6 ) , M 1 M 3 ⃗ = ( − 2 , 3 , − 1 ) ∴ n ⃗ = M 1 M 2 ⃗ × M 1 M 3 ⃗ = ∣ i ⃗ j ⃗ k ⃗ − 3 4 − 6 − 2 3 − 1 ∣ = 14 i ⃗ + 9 j ⃗ − k ⃗ ∴ 平面方程为 14 ( x − 2 ) + 9 ( y + 1 ) − ( z − 4 ) = 0 即 14 x + 9 y − z − 15 = 0 解：设平面的法线向量\vec n,则\vec n\perp \vec{M_1M_2},且\vec n\perp\vec{M_1M_3}\\ \vec{M_1M_2}=(-3,4,-6),\vec{M_1M_3}=(-2,3,-1)\\ \therefore \vec n=\vec{M_1M_2}\times\vec{M_1M_3}= \begin{vmatrix} \vec i&\vec j&\vec k\\ -3&4&-6\\ -2&3&-1\\ \end{vmatrix}\\ =14\vec i+9\vec j-\vec k\\ \therefore 平面方程为 14(x-2)+9(y+1)-(z-4)=0\\ 即 14x+9y-z-15=0 解：设平面的法线向量n ,则n ⊥M1​M2​ ​,且n ⊥M1​M3​ ​M1​M2​ ​=(−3,4,−6),M1​M3​ ​=(−2,3,−1)∴n =M1​M2​ ​×M1​M3​ ​= ​i −3−2​j ​43​k −6−1​ ​=14i +9j ​−k ∴平面方程为14(x−2)+9(y+1)−(z−4)=0即14x+9y−z−15=0

3 平面的一般方程

• 平面的点法式方程$\Rightarrow$ 平面的一般方程

已知平面的点法式方程：$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$,则
$$\begin{gathered} Ax+By+Cz-(A{x}_0+B{y}_0+C{z}_0)=0 \\ 令D=-(A{x}_0+B{y}_0+C{z}_0)=0 \\ 即Ax+By+Cz+D=0(3-4) \end{gathered}$$
方程（3-4）即为平面的一般方程。

• 平面的一般方程$\Rightarrow$ 平面的点法式方程

已知平面的一般方程$Ax+By+Cz+D=0$,则
$$\begin{gathered} 任取平面上一点(x_0,y_0,z_0),则该点满足上述方程，有 \\ A{x}_0+B{y}_0+C{z}_0+D=0,两个方程相减，得 \\ A(x-x_0)+B(y-y_0)+C(z-z_0)=0 \end{gathered}$$

注：

1. $D=0\iff 平面过原点，即Ax+By+Cz=0$

2. $A=0\iff 平面平行(或包含)x轴$

   • $B=0\iff 平面平行(或包含)y轴$
   • $C=0\iff 平面平行(或包含)z轴$

3. $A=B=0\iff 平面平行(或者重合于)xOy平面$

   • $B=C=0\iff 平面平行(或者重合于)yOz平面$
   • $A=C=0\iff 平面平行(或者重合于)xOz平面$

4. $A=D=0\iff 平面包含x轴$

   • $B=D=0\iff 平面包含y轴$
   • $C=D=0\iff 平面包含z轴$

5. $A=B=D=0\iff 平面xOy$

• $B=C=D=0\iff 平面yOz$
• $A=C=D=0\iff 平面xOz$

例3 求过x轴和点$(4,-3,-1)的平面方程。
$$\begin{gathered} 解：平面方程Ax+By+Cz+D=0 \\ \because 平面过x轴则A=D=0 \\ 平面过点(4,-3,-1)，则 \\ -3B-C=0,C=-3B,带入原方程 \\ By-3Bz=0,即y-3z=0 \end{gathered}$$
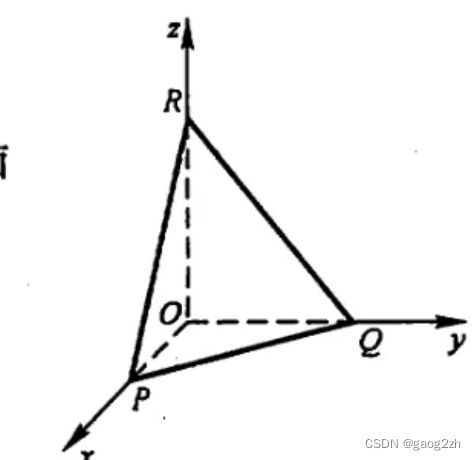
例4 设一平面与x，y，z轴的交点依次为$P(a,0,0),Q(0,b,0),R(0,0,c)$三点，求着平面的方程（$a\ne 0,b\ne 0,c\ne 0$）

$$\begin{gathered} 解：三点都满足平面的一般方程，带入 \\ \{\begin{array}{l}aA+D=0\\ bB+D=0\\ cC+D=0\end{array} \\ 解方程组得,A=-\frac{D}{a},B=-\frac{D}{b}，C=-\frac{D}{c},带入原方程 \\ -\frac{D}{a}x-\frac{D}{b}y-\frac{D}{c}z+D=0 \\ 即\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \end{gathered}$$
方程$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1(3-7)$称为平面的截距式方程，$a,b,c$叫做平面在$x,y,z$轴上的截距。

4 两平面的夹角

4.1 两平面夹角的定义

两平面的法线向量的夹角（通常指锐角或者直角）称为两平面的夹角。

4.2 夹角的余弦公式

设平面${\pi }_1法线向量n_1=(A_1,B_1,C_1),平面{\pi }_2的法线向量n_2=(A_2,B_2,C_2)$,则

​ $\cos \theta =\frac{|A_1{A}_2+B_1{B}_2+C_1{C}_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\cdot \sqrt{A_2^2+B_2^2+C_2^2}}$

注：

• 两平面垂直$\iff A_1{A}_2+B_1{B}_2+C_1{C}_2=0$
• 两平面平行或者重合$\iff \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}$

例 5 求两平面$x-y+2z-6=0和2x+y+z-5=0$的夹角。
$$\begin{gathered} 解：由两平面余弦夹角公式有 \\ \cos \theta =\frac{|2-1+2|}{\sqrt{1+1+4}\cdot \sqrt{4+1+1}}=\frac{1}{2} \\ 所以\theta =\frac{\pi }{3} \end{gathered}$$
例6 一平面过两点$M_1(1,1,1)和M_2(0,1,-1)$且垂直于平面$x+y+z=0$,求它的方程。
$$\begin{gathered} 解：设所求平面的法线向量n=(A,B,C),则n\perp M_1{M}_2 \\ {M}_1{M}_2=(-1,0,-2) \\ 即-A-2C=0(6-1) \\ \because 平面垂直于x+y+z=0,有 \\ A+B+C=0(6-2) \\ 由(6-1)和(6-2)得A=-2C,B=C \\ 有平面点法式方程，所求平面为 \\ A(x-1)+B(y-1)+C(z-1)=0 \\ A=-2C,B=C带入上式，得平面方程 \\ 2x-y-z=0 \end{gathered}$$

4.3 点到平面的距离

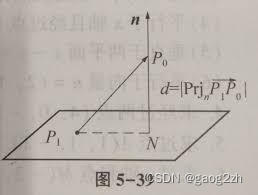
例7 设点$P_0(x_0,y_0,z_0)是平面Ax+By+Cz+D=0$外一点，求点$P_0$到这平面的距离，如下图4.3-1所示

$$\begin{gathered} 解：平面法线向量n=(A,B,C) \\ 任取平面一点P_1(x_1,y_1,z_1),点P_0到平面的距离及为p_1{P}_0在法线上的投影 \\ d=|Pr{j}_n{P}_1{P}_0|=\frac{|n\cdot P_1{P}_0|}{|n|} \\ =\frac{A(x_0-x_1)+B(y_0-y_1)+C(z_0-z_1)}{\sqrt{A^2+B^2+C^2}} \\ =\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}} \end{gathered}$$

• 点$P_0(x_0,y_0,z_0)到平面Ax+By+Cz+D=0的距离公式为：\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}$

注：

• 若两平面方程为$Ax+Bx+Cz+D_1=0和Ax+Bx+Cz+D_2=0$，则两平面平行；两平面距离$d=\frac{|D_1-D_2|}{\sqrt{A^2+B^2+C^2}}$

结语

❓QQ:806797785

⭐️文档笔记地址：https://gitee.com/gaogzhen/math

参考：

[1]同济大学数学系.高等数学 第七版 下册[M].北京:高等教育出版社,2014.7.p23-29.

[2]同济七版《高等数学》全程教学视频[CP/OL].2020-04-16.p53.