数据结构常用知识点整理(java版)(--修改中--)
目录
一、逻辑结构
1、栈
2、队列
顺序队列
循环队列
链式队列 (相当于只能尾进头出的单链表)
双端队列 (Deque)
3、数组
4、链表
5、树
二叉树
满二叉树
完全二叉树
二叉查找树: (ADT Tree)
红黑树:
B树:
AVL树:(平衡二叉树)
6、图
7、堆
二叉堆( 优先队列 )
d-堆
左式堆
斜堆
8、散列表
1、包装类(8种)
2、String类
3、StringBuffer类
4、StringBuilder类
5、Math类
6、Arrays类
7、System类
8、BigInteger类
9、BigDecimal类
10、日期类
刷题时,要解决一道算法题,首先下手的,就是确定数据该放进哪种空间结构里,怎样才能花费最少的时间和空间来达到目的。是用树呢,还是链表,还是队列…… 为了帮助我在做题时更加清晰、全面地思考,故作此文梳理数据结构的知识。
资源合集:
计算机黑皮丛书:191本
跳转中...
验证码:1111
电子书下载网站:
安娜的档案
逻辑结构:(两种)
- 线性结构
- 非线性结构
存储结构:
- 顺序存储
- 链式存储
- 索引存储
- 散列存储
数据运算:
(常见增删改查四种)
- 检索
- 获取
- 插入
- 删除
- 更新
- 排序
数据结构:(八种)
- 栈(Stack)
- 队列(Queue)
- 数组(Array)
- 链表(Linked List)
- 树(Tree)
- 图(Graph)
- 堆(Heap)
- 散列表(Hash)
一、逻辑结构
第一种:线性结构
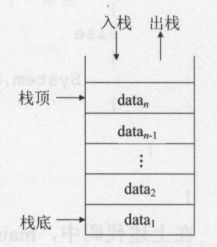
1、栈
特点:
保存和取出数据都只能从栈结构的一端进行。
栈结构是按照“后进先出(Last In First Out)”的原则处理数据的。
基本操作:
- Stack
stack=new Stack<>();//创建栈,T为栈中存储的数据的类型 - stack.push(a);//把元素a压入栈中
- stack.pop();//弹出栈顶元素
- stack.peek();//只读取栈顶数据,不弹出
- stack.empty();判断栈是否为空
- stack.search(a);//返回元素a在栈里的下标(从1开始算)
- stack.top();//返回当前为空的、可以存放数据元素的下标(从栈底往栈顶开始找)
3)栈的顺序结构的数组实现:
package com.itheima;
class DATA {//栈内存储的数据类型为DATA
String name;
int age;
}
class StackType{
static final int MAXLEN=50;//栈的大小
DATA[] data=new DATA[MAXLEN+1];//存储数据元素
int top;//栈顶
StackType STInit(){//栈的初始化
StackType p;
if((p=new StackType())!=null){//申请栈内存
p.top=0;//设置栈顶为0
return p;//返回指向栈的引用
}
return null;
}
boolean STIsEmpty(StackType s){//判断栈是否为空
boolean t;
t=(s.top==0);
return t;
}
boolean STIsFull(StackType s){//判断栈是否已满
boolean t;
t=(s.top==MAXLEN);
return t;
}
void STClear(StackType s){//清空栈
s.top=0;
}
void STFree(StackType s){//释放栈所占用空间
if(s!=null){
s=null;
}
}
int PushST(StackType s,DATA data){//入栈操作
if((s.top+1)>MAXLEN){
System.out.println("栈溢出!\n");
return 0;
}
s.data[++s.top]=data;//将元素入栈
return 1;
}
DATA PopST(StackType s){//出栈操作
if(s.top==0){
System.out.println("栈为空!\n");
System.exit(0);
}
return (s.data[s.top--]);
}
DATA PeekST(StackType s){//出栈操作
if(s.top==0){
System.out.println("栈为空!\n");
System.exit(0);
}
return (s.data[s.top]);
}
}4)栈的链式结构实现
//栈的结构:
//定义链栈的结点类
public class SNode{
public Data data;//要存放到栈中的元素
public SNode next;//栈顶指针
//构造器省略
}//链栈
public class LinkedStack{
public SNode top;//栈顶指针
public int count;//链栈结点数
//构造器省略
}//进栈
boolean Push(StackType s,Data data){
SNode p=(SNode)malloc(sizeof(SNode));//给新元素分配空间
p.data=data;//新元素的值
p.next=s.top;//p的后继指向栈顶元素
s.top=p;//栈顶指针指向新的元素
s.count++;//统计栈中元素
return true;
}//出栈
boolean Pop(StackType s,Data data){
if(s.top==NULL) return false;//空栈,直接返回
data=s.top.data;//栈顶元素值
SNode p=s.top;//辅助指针,保存栈顶元素
s.top=s.top.next;//栈顶指针后移
STFree(p);//释放被删除数据的存储空间
s.count--;//栈中元素个数减一
return true;
}5)两栈共享空间
只要两个栈的栈顶指针不见面,两个栈就还可以使用
当top1==-1时,栈1为空
当top2==栈1的长度 时,栈2为空
当top1+1==top2时,栈满
//两个栈的结构
public class SqDoubleStack{
public Data data[MAXLen];
int top1;//栈1的栈顶指针
int top2;//栈2的栈顶指针
//构造器省略
}//入栈
boolean Push(SqDoubleStack s,Data data,int stackNumber){//参数stackNumber用于判断是用哪个栈
if(s.top1+1==s.top2) //栈已满
return false;
if(stackNumber==1)//栈1有元素进栈
s.data[++s.top1]=data;//top1指针先后移一位,再给数组赋值
else if(stackNumber==2)//栈2有元素进栈
s.data[--s.top2]=data;
return true;
}//出栈
boolean Pop(SqDoubleStack s,Data data,int stackNumber){
if(stackNumber==1){
if(s.top1==-1)//栈1是空栈
return false;
data=s.data[s.top1--];//将栈1的栈顶元素出栈
}
else if(stackNumber==2){
if(s.top2==MAXLEN)//栈2是空栈
return false;
data=s.data[s.top2++];//将栈2的栈顶元素出栈
}
return true;
}2、队列
特点:
- 队头只能进行删除操作,队尾只能进行插入操作。
- 队列结构是按照“先进先出(First In First Out)”的原则处理数据的。
常用单词:
- 尾部插入:offerLast
- 头部插入:offerFirst
- 尾部移除:pollLast
- 头部移除:pollFirst
- 尾部获取:peekLast
- 头部获取:peekFirst
- 入队:enqueue
- 出队:dequeue
常用方法:
注:前面一组方法操作失败后,会抛出异常,后一组方法失败后,会返回特殊值
Queue queue=new LinkedList<>();//创建一个T类型的队列
queue.add(a);//把元素a加入队列,加入成功就返回true,加入失败抛出异常
queue.remove();//取出队头的元素
queue.element();//读取队头的元素,但不移除
queue.offer(a);//把元素a加入队列
queue.poll();//取出队头的元素,如果队列为空就返回null
queue.peek();//取出队头的元素,如果队列为空就返回null
queue.size();//获取队列长度 顺序队列
package com.itheima;
import java.util.Scanner;
class DATA{
String name;
int age;
}
class SQType{
static final int QUEUELEN=15;
DATA[] data=new DATA[QUEUELEN];//队列数组
int head;//队头
int tail;//队尾
SQType SQTypeInit(){//队列初始化
SQType q;
if ((q = new SQType()) != null) {//申请内存
q.head=0;//设置队头
q.tail=0;//设置队尾
return q;
}else {
return null;//返回空
}
}
int SQTypeIsEmpty(SQType q){//判断空队列
int temp=0;
if(q.head==q.tail) {
temp=1;
}
return temp;
}
int SQTypeIsFull(SQType q){//判断满队列
int temp=0;
if(q.tail==QUEUELEN){
temp=1;
}
return temp;
}
void SQTypeClear(SQType q){//清空队列
q.head=0;//设置队头
q.tail=0;//设置队尾
}
void SQTypeFree(SQType q){//释放队列
if(q!=null){
q=null;
}
}
int InSQType(SQType q,DATA data){//入队列
if(q.tail==QUEUELEN){
System.out.print("队列已满,操作失败!\n");
return 0;
}else{
q.data[q.tail++]=data;//将元素入队列
return 1;
}
}
DATA OutSQType(SQType q){//出队列
if(q.head==q.tail){
System.out.print("\n队列已空,操作失败!\n");
System.exit(0);
}else{
return q.data[q.head++];
}
return null;
}
DATA PeekSQType(SQType q){//读队头结点数据
if(SQTypeIsEmpty(q)==1){
System.out.print("\n空队列!\n");
return null;
}else{
return q.data[q.head];
}
}
int SQTypeLen(SQType q){//计算队列长度
int temp;
temp=q.tail-q.head;
return temp;
}
}循环队列
关键代码:
判断队列是空还是满:
- 法一:设置标志位flag,当flag=0且rear==front时认为队列为空;当flag=1且rear==front时认为队列为满。
- 法二:当front==rear时,认为队列为空;当队列满时,令数组中仍然保留一个空余单元,认为此时队列为满
- 入队(rear指针后移):rear=(rear+1)%MaxSize
- 出队(front指针后移):front=(front+1)%MaxSize
- 计算队列长度公式:(rear-front+MaxSize)%MaxSize
总结:判断队列空满情况,然后决定是否入出队
//入队
boolean EnQueue(SQType q,DATA data){
if((q.rear+1)%MaxSize==q.front)//队列已满
return false;
q.data[q.rear]=data;//将元素data赋值给队尾
q.rear=(q.rear+1)%MaxSize;//rear指针向后移一位
return true;
}//出队
boolean DeQueue(SQType q,DATA data){
if(q.front==q.rear)//队列已满
return false;
data=q.data[q.front];//将队头元素赋值给元素data
q.front=(q.front+1)%MaxSize;//front指针向后移一位
return true;
}链式队列 (相当于只能尾进头出的单链表)
//链式队列的结构
//结点结构
public class QNode{
Data data;//队列内存储的元素类型
QNode next;//队列结点
//构造器省略
}//队列的链表结构
public class LinkedQueue{
QNode front,rear;//队头、队尾指针
//构造器省略
}//入队
boolean EnQueue(LinkedQueue q,Data data){
SNode s=(SNode)malloc(sizeof(QNode));//为新元素分配存储空间
if(!s)//存储分配失败
return false;
s.data=data;//把新元素存入当前结点
s.next=NULL;//把当前结点当成队尾结点,斩断后继
q.rear.next=s;//原队尾结点的后继指向当前新结点
q.rear=s;//把当前的s结点设置为队尾结点,更新队尾指针的指向
return true;
}
/*
处理四个地方:
1、旧队尾结点的后继
2、新队尾结点的前接
3、新队尾结点的后继
4、更新队尾指针的指向
*///出队 (在链表尾部插入结点)
boolean DeQueue(LinkedQueue q,Data data){
QNode p;
if(q.front==q.rear)//队列为空
return false;
p=q.front.next;//将欲删除的队头结点暂存给p
data=p.data;//存储p结点的值,可能需要返回该值
q.front.next=p.next;//现在头结点(不存储元素)的后继指向原来队头结点(存储元素)的后继,
if(q.rear==p)//若队头是队尾,则删除后将rear指向头结点
q.rear=q.front;
SQTypeFree(p);//释放原头结点的存储空间
return true;
} 在可以确定队列长度最大值时,建议用循环队列;如果无法预估队列的长度时,则用链队列。
双端队列 (Deque)
允许在两端进行访问的队列,LinkedList是典型的双端队列实现
Deque
queue = new ArrayDeque ();
//接口定义
public interface Deque {
boolean offerFirst(E e);
boolean offerLast(E e);
E pollFirst();
E pollLast();
E peekFirst();
E peekLast();
boolean isEmpty();
boolean isFull();
}
//链表实现
/**
* 基于环形链表的双端队列
* @param 元素类型
*/
public class LinkedListDeque implements Deque, Iterable {
@Override
public boolean offerFirst(E e) {//头部插入
if (isFull()) {
return false;
}
size++;
Node a = sentinel;
Node b = sentinel.next;
Node offered = new Node<>(a, e, b);
a.next = offered;
b.prev = offered;
return true;
}
@Override
public boolean offerLast(E e) {//尾部插入
if (isFull()) {
return false;
}
size++;
Node a = sentinel.prev;
Node b = sentinel;
Node offered = new Node<>(a, e, b);
a.next = offered;
b.prev = offered;
return true;
}
@Override
public E pollFirst() {//头部移除
if (isEmpty()) {
return null;
}
Node a = sentinel;
Node polled = sentinel.next;
Node b = polled.next;
a.next = b;
b.prev = a;
size--;
return polled.value;
}
@Override
public E pollLast() {//尾部移除
if (isEmpty()) {
return null;
}
Node polled = sentinel.prev;
Node a = polled.prev;
Node b = sentinel;
a.next = b;
b.prev = a;
size--;
return polled.value;
}
@Override
public E peekFirst() {//头部读取,但不移除
if (isEmpty()) {
return null;
}
return sentinel.next.value;
}
@Override
public E peekLast() {//尾部读取,但不移除
if (isEmpty()) {
return null;
}
return sentinel.prev.value;
}
@Override
public boolean isEmpty() {//判断是否为空队
return size == 0;
}
@Override
public boolean isFull() {//判断是否为满队
return size == capacity;
}
@Override
public Iterator iterator() {//迭代器,用于遍历队列,类似于指针
return new Iterator() {
Node p = sentinel.next;
@Override
public boolean hasNext() {
return p != sentinel;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
static class Node {//结点结构
Node prev;
E value;
Node next;
public Node(Node prev, E value, Node next) {
this.prev = prev;
this.value = value;
this.next = next;
}
}
Node sentinel = new Node<>(null, null, null);
int capacity;
int size;
public LinkedListDeque(int capacity) {
sentinel.next = sentinel;
sentinel.prev = sentinel;
this.capacity = capacity;
}
} //数组实现
import java.util.Deque;
/**
* 基于循环数组实现, 特点
*
* - tail 停下来的位置不存储, 会浪费⼀个位置
*
* @param
*/
public class ArrayDeque1 implements Deque, Iterable {
@Override
public boolean offerFirst(E e) {//头部插入
if (isFull()) {
return false;
}
head = dec(head, array.length);
array[head] = e;
return true;
}
@Override
public boolean offerLast(E e) {//尾部插入
if (isFull()) {
return false;
}
array[tail] = e;
tail = inc(tail, array.length);
return true;
}
@Override
public E pollFirst() {//头部移除
if (isEmpty()) {
return null;
}
E e = array[head];
array[head] = null;
head = inc(head, array.length);
return e;
}
@Override
public E pollLast() {//尾部移除
if (isEmpty()) {
return null;
}
tail = dec(tail, array.length);
E e = array[tail];
array[tail] = null;
return e;
}
@Override
public E peekFirst() {//头部读取,但不移除
if (isEmpty()) {
return null;
}
return array[head];
}
@Override
public E peekLast() {//尾部读取,但不移除
if (isEmpty()) {
return null;
}
return array[dec(tail, array.length)];
}
@Override
public boolean isEmpty() {//判断是否为空队列
return head == tail;
}
@Override
public boolean isFull() {//判断是否为满队列
if (tail > head) {
return tail - head == array.length - 1;
} else if (tail < head) {
return head - tail == 1;
} else {
return false;
}
}
@Override
public Iterator iterator() {//迭代器,用于遍历队列
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E e = array[p];
p = inc(p, array.length);
return e;
}
};
}
E[] array;
int head;
int tail;
@SuppressWarnings("unchecked")
public ArrayDeque1(int capacity) {//数组结构
array = (E[]) new Object[capacity + 1];
}
static int inc(int i, int length) {
if (i + 1 >= length) {
return 0;
}
return i + 1;
}
static int dec(int i, int length) {
if (i - 1 < 0) {
return length - 1;
}
return i - 1;
}
} 3、数组
特点:
- 数组是存储同一类型数据的数据结构
- 使用数组时需要先定义数组的大小和存储数据的数据类型
- 数组大小是固定的(一旦创建后,无法更改)。如果元素个数超过了数组的容量,就需要创建一个新的更大的数组,并将当前数组中的元素复制到新数组中。
- 数组分为一维数组和多维数组
- 数组的数据按顺序存储,逻辑地址和物理地址都是连续的(二维数组的存储顺序有两种:行优先和列优先)
矩阵压缩:
定义:某些二维数组的元素间有特殊的规律,所以只需要存储其中的一部分,而另一部分的存储地址可以通过相应的算法计算出来。
分类:一、对称矩阵;二、稀疏矩阵;三、三角矩阵
[] array=new [length];
[][] array=new [row.length][column.length]; 第二种:非线性结构
4、链表
特点:
- 每个结点都由数据元素和对链表中下一个结点的链组成
- 头结点(哨兵节点):不存储数据,通常用作头尾,用来简化边界判断,使得第一个元素也像其他元素一样有前驱结点。
- 元素存储上不连续
- List
list=new ArrayList<>(); - list.add(index,e);//在下标为index处插入元素e
- list.add(e);//在链表尾部插入元素a
- list.clear();//移除链表中所有的元素
- list.contains(e);//链表中是否包含元素e
- list.equals(e);//判断两个对象是否相等
- list.get(index);//获取下标为index的链表中的元素
- list.indexOf(e);//获取元素e在链表中的下标
- list.isEmpty();//判断链表是否为空
- list.remove(index);//删除链表中下标为index的元素
- list.remove(e);//删除链表中的元素e
- list.set(index,e);//修改链表中下标为index处的元素为e
- list.size();//获取链表的大小
- list.toArray();//把链表转成数组返回
//结点类
public class SinglyLinkedList {
private Node head; // 头部节点
private static class Node { // 节点类
int value;
Node next;
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
}
}单向链表:
双向链表:
特点:
通过每个结点存储两个链,双向链表允许双向遍历。
循环链表:
5、树
特点:
在一个树结构中,有且仅有根结点没有直接前驱,其余的结点都有且仅有一个直接前驱,但可以有任意多个直接后继
相关概念:
- 父结点和子结点:每个结点子树的根称为该结点的子结点,相应的,该结点称为其子结点的父结点。
- 兄弟结点:具有同一父结点的结点称为兄弟结点。
- 结点的度:一个结点所包含子树的数量。
- 树的度:是指该树所有结点中最大的度。
- 叶结点:树中度为零的结点称为叶结点或终端结点。
- 分支结点:树中度不为零的结点称为分支结点或非终端结点。
- 结点的层数:结点的层数从树根开始计算,根结点为第1层、依次向下为第2、3、n层(树是一种层次结构,每个结点都处在一定的层次上)。
- 树的深度:树中结点的最大层数称为树的深度。
- 有序树:若树中各结点的子树(兄弟结点)是按一定次序从左向右排列的,称为有序树。
- 无序树:若树中各结点的子树(兄弟结点)未按一定次序排列,称为无序树。
- 森林(forest):n(n>0)互不相交的树的集合。
二叉树
特点:
- 每个结点最多只能有两个子结点(左子树和右子树)
- 节点 = 元素的信息 + 两个到其他节点的引用(left和right)
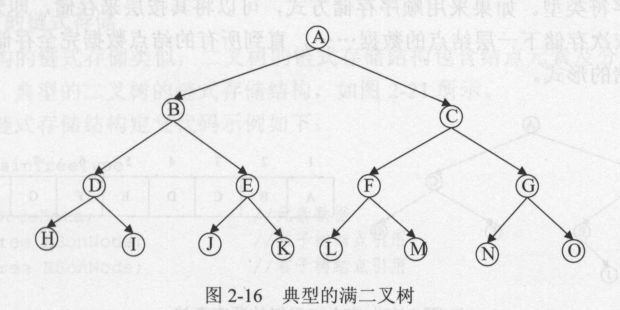
满二叉树
特点:在二叉树中除最下一层的叶结点外,每层的结点都有两个子结点。
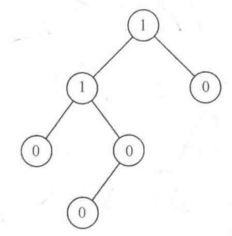
完全二叉树
特点:在二叉树中除二叉树最后一层外,其他各层的结点数都达到最大个数,且最后一层叶结点按照从左向右的顺序连续存在,只缺最后一层右侧若干结点。
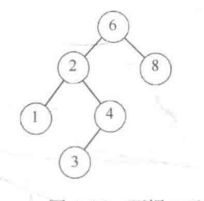
二叉查找树: (ADT Tree)
特点:
对于树中的每个节点X,它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项。意味着二叉查找树上所有的元素都可以用某种一致的方式排序。
TreeNode root=new TreeNode;
root.getSize();//获取树的结点数
root.getRoot();//获取树的根结点
root.getParent(x);//获取结点x的父结点
root.getFirstChild(x);//获取结点x的第一个孩子
root.getNextSibling(x);//获取结点x的下一个兄弟结点,如果x是最后一个孩子,则返回空
root.getHeight(x);//获取以x为根的树的高度
root.insertChild(x,child);//将结点child为根的子树插入树中,作为结点x的子树
root.deleteChild(x,i);//删除结点x的第i棵子树
root.preOrder(x);//先序遍历x为根的树
root.postOrder(x);//后序遍历x为根的树
root.levelOrder(x);//按层遍历x为根的树红黑树:
B树:
AVL树:(平衡二叉树)
特点:
- 左右子树具有相同的高度
- 插入一个节点可能会破坏AVL树的特性,但可以通过修正来恢复平衡的性质,称为旋转。
- 插入的节点在左右边缘时,用单旋转,用中间时用双旋转。
- 树太深时,做单旋转没有减低它的深度时,就用双旋转。
遍历二叉树:
- 先序遍历:根——》左—》右
- 中序遍历:左——》根——》右
- 后序遍历: 左——》右——》根
遍历的思路:
- 层序遍历:广度优先(隐式地维护了栈空间)
- 递归遍历:深度优先(显式地模拟出栈空间)
- Morris遍历:强行把一棵二叉树改成一段链表结构(没有使用任何辅助空间)
递归函数实现:
1、终止条件:当前节点为空时
2、函数内:
- 前序遍历:要做的事的代码 - 左-右
- 中序遍历:左-要做的事的代码 - 右
- 后序遍历:左-右-要做的事的代码
Morris遍历算法步骤(假设当前遍历到的节点为x):
- 如果x无左孩子,先将x的值加入答案数组,再访问x的右孩子,即x=x.right。
- 如果x有左孩子,则找到x左子树上最右的节点(即左子树中序遍历的最后一个节点,x在中序遍历中的前驱节点),记为predecessor。
- 如果predecessor的右孩子为空,则将其右孩子指向x,然后访问x的左孩子,即x=x.left
- 如果predecessor的右孩子不为空,则此时其右孩子指向x,说明已经遍历完x的左子树,我们将predecessor的右孩子置空,将x的值加入答案数组,然后访问x的右孩子,即x=x.right
6、图
7、堆
二叉堆( 优先队列 )
特点:
应用:
找到第k个最小元素
法一:将N个元素读入一个数组。然后对该数组应用buildHeap算法。最后,执行次deleteMin操作。从该堆最后提取的元素就是我们的答案。
法二:维持一个k个最大元素的集合S,该集合为堆结构,维护根处的最小元。
基本的堆操作:
insert(插入)
上滤:
为将一个元素X插入到堆中,我们在下一个可用位置创建一个空穴,否则该堆将不是完全树。如果可以放在该空穴中而并不破坏堆的序,那么插入完成。否则,我们把空穴的父节点上的元素移入该空穴中,这样,空穴就朝着根的方向上冒一步。继续该过程直到X能被放入空穴中为止。
public void insert(AnyType x){
if(currentSize==array.length-1)
enlargeArray(array.length*2+1);//扩容
int hole = ++currentSize;//创建空穴
for(array[0]=x;x.compareTo(array[hole/2])<0;hole/=2)
arr[hole]=array[hole/2];//空穴上滤
array[hole]=x;//空穴插入值
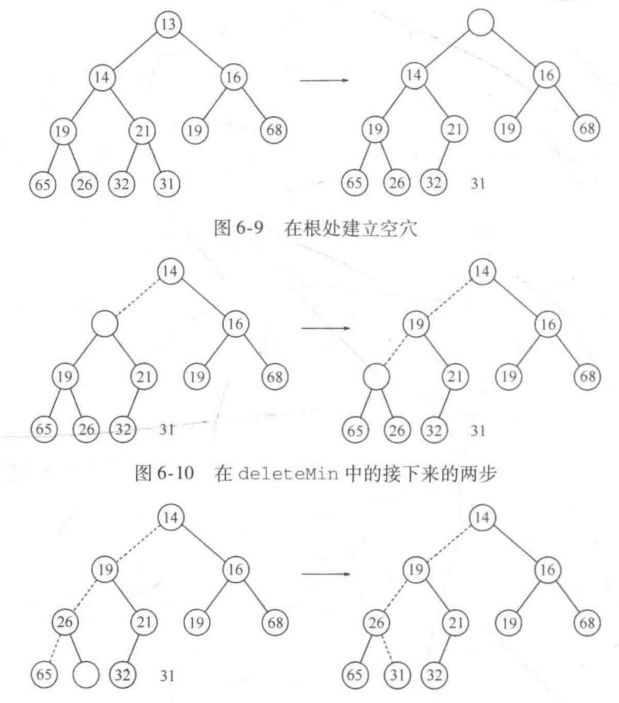
}deleteMin(删除最小元)
下滤:
当删除一个最小元时,要在根节点建立一个空穴。因此我们将空穴的两个儿子中较小者移入空穴,这样就把空穴向下推了一层重复该步骤直到X可以被放人空穴中。因此,我们的做法是将X置入沿着从根开始包含最小儿子的一条路径上的一个正确的位置。
public AnyType deleteMin(){//移除或返回最小元
if(isEmpty())
throw new UnderflowException();
AnyType minItem=findMin();
array[1]=array[currentSize--];
percolateDown(1);
return minItem;
}
public void percolateDown(int hole){//下滤
int child;
AnyType tmp=array[hole];//创建空穴
for(;hole*2<=currentSize;hole=child){
child=hole*2;
if(child!=currentSize && array[child+1].compareTo(array[child])<0)
child++;
if(array[child].compareTo(tmp)<0)
array[hole]=array[child];
else
break;
}
array[hole]=tmp;
}
buildHeap(构建堆)
有时二叉堆是由一些项的初始集合构造而得。这种构造方法以N项作为输入,并把它们放到一个堆中。显然,这可以使用N个相继的insert操作来完成。
public BinaryHeap(AnyType[] items){//从零开始构建二叉堆
currentSize=items.length;
array=(AnyType[]) new Comparable[(currentSize+2)*11/10];
int i=1;
for(AnyType item:items)
array[i++]=item;
buildHeap();
}
private void buildHeap(){//把二叉堆通过下滤从无序变成有序
for(int i=currentSize/2;i>0;i--)
percolateDown(i);//下滤
}d-堆
特点:
左式堆
特点:
- 左式堆也是二叉树。
- 左式堆和二叉堆唯一的区别是:左式堆不是理想平衡的(perfectlybalanced),而实际上趋向于非常不平衡。
- 因为左式堆走向于加深左路径,所以右路径的长度小于等于左路径的长度
- 基本操作:合并
斜堆
特点:
斜堆是具有堆序的二叉树,但不存在对树的结构限制(右路径可以任意长)
基本操作:合并
8、散列表
特点:
- 以常数平均时间执行增删改除操作
- 元素间是无序的
哈希表(Hash Table):
- 一种基于哈希算法实现的Dictionary类的子类,可以存储键值对
- 其中键和值都不能为null,键必须唯一
- Hashtable是线程安全的,但是性能较差,不推荐使用
哈希冲突:
正常情况应该是一个关键字映射到一个地址(散列函数),哈希冲突则是同一个地址对应不止一个关键字。
哈希集合(Hash Set):
- 一种基于哈希算法实现的Set接口的实现类
- 可以存储不重复的元素
- 其中元素可以为null
- HashSet是非线程安全的,不保证元素的顺序
//哈希集合常用方法:
Set set=new HashSet<>();//创建一个T类型的哈希集合
set.add(e);//添加元素
set.clear();//清空哈希集合
set.contains(e);//哈希集合中是否包含元素e,返回boolean值
set.isEmpty();//哈希集合中是否为空,返回boolean值
set.iterator();//返回一个迭代器
set.remove(e);//删除元素e
set.size();//获取哈希集合的大小
set.toArray();//返回一个包含哈希集合所有元素的数组 哈希映射(Hash Map):
- 一种基于哈希算法实现的Map接口的实现类,可以存储键值对
- 其中键和值都可以为null,但是键必须唯一
- HashMap是非线程安全的,不保证元素的顺序
//哈希映射常用方法:
Map map=new HashMap<>();//创建一个哈希映射
map.clear();//清空哈希映射
map.containsKey(key);//是否包括元素key,返回boolean值
map.containsValue(value);//是否包括元素value,返回boolean值
map.get(key);//返回键key对应的值value
map.isEmpty();//哈希映射是否为空,返回boolean值
map.put(key,value);//把键值对存入哈希映射
map.remove(key);//移除key这对键值对
map.size();//获取哈希映射的大小
map.getOrDefault(key,value);//如果map中包含key,就获取对应的值,否则返回value //获取哈希映射中的键或值
map.entrySet();//返回一个Set类型的对象,该对象的元素是各个键值对(Entry)形成的对象,可以通过遍历这个Set对象来获取每个键值对。如下;
Map map = new HashMap<>();
map.put("A", 1);
map.put("B", 2);
map.put("C", 3);
Set> entrySet = map.entrySet();
for (Map.Entry entry : entrySet) {
System.out.println(entry.getKey() + ":" + entry.getValue());
}
map.keySet();//获取map中所有的key组成的集合。它返回一个Set类型的集合,其中包含的是该map中所有的键
HashMap hashmap = new HashMap();
hashmap.put("apple", 1);
hashmap.put("banana", 2);
hashmap.put("orange", 3);
Set keys = hashmap.keySet();
for (String key : keys) {
System.out.println(key);
}
二、常用类
在创建数据的空间结构时,通常也要定下它要存储的数据类型,如String类型有什么方法可以用,StringBuffer类型的又有什么方法可以用,想要用某个可以追加数据的方法,又是哪个数据类型的。下面针对这方面做个知识梳理。
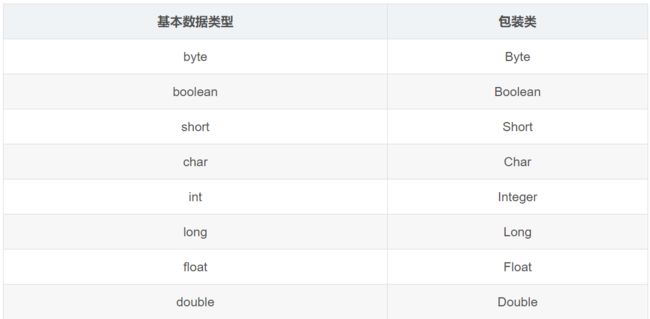
1、包装类(8种)
(1) 包装类常用方法
1)Integer类
Integer.MIN_VALUE;//返回最小值
Integer.MAX_VALUE;//返回最大值2)Character类
Character.isDigit('a');//判断是不是数字
Character.isLetter('a');//判断是不是字母
Character.isUpperCase('a');//判断是不是大写
Character.isLowerCase('a');//判断是不是小写
Character.isWhitespace('a');//判断是不是空格
Character.toUpperCase('a');//转成大写
Character.toLowerCase('A');//转成小写
Char c='0';
int num=(int)c-48;//0的ASCII码为48,char型转成int型(2)基本数据类型和包装类的相互转换(自动装箱和自动拆箱)
//以int为例
//自动装箱 int->Integer
Integer integer=n1;
//自动拆箱 Integer->in
int n2=interger;(3)String类和包装类的相互转换
//以Integer为例
String string1="111111";
//String -> Integer,字符串转成数字
//方式一
Integer integer=Integer.parseInt(string1);
//方式二
Integer integer=new Integer(string1);
//Integer -> String,数字转成字符串
//方式一
String string2=integer.toString();
//方式二
String string2=String.valueOf(integer);2、String类
//创建String对象
//方式一:直接赋值
String string="11111";
//方式二:调用构造器
String string=new String("11111");
string.equals(string2);//比较内容是否相同,区分大小写,返回boolean值
string.equalsIgnoreCase(string2);//比较内容是否相同,忽略大小写
string.length();//获取字符的个数,字符串的长度
string.indexOf('1');//获取字符在字符串对象中第一次出现的索引,索引从 0 开始,如果找不到,返回-1
string.lastIndexOf('1');//获取字符在字符串中最后一次出现的索引,索引从 0 开始,如果找不到,返回-1
string.substring(0,1);//截取指定索引范围的子串,前闭后开
string.trim();//去除字符串前后的空格
string.charAt(0);//获取指定索引处的字符
string.toUpperCase();//转换成大写
string.toLowerCase();//转换成小写
string.concat(string2);//拼接字符串
string.replace("被替换","替换");//方法执行后返回的结果才是替换过的,对原字符串没有任何影响
string.split(" ");//分割字符串, 如果有特殊字符,需要加入转义符 \ 如 | \\等
string.compareTo(string2);//比较两个字符串的大小,如果前者大,返回正数;后者大,返回负数,如果相等,返回 0
string.toCharArray();// 转换成字符数组
string.format();//格式字符串,%s%c%d%f
3、StringBuffer类
(1)常用方法:
StringBuffer stringbuffer=new StringBuffer();
stringbuffer.append(string);//后面追加字符或字符串
stringbuffer.delete(start,end);//删除索引在[start,end)区间内的字符
stringbuffer.replace(start,end,string);//用string的内容替换索引在[start,end)区间内的字符串
stringbuffer.indexOd(string);//查找指定的子串在字符串第一次出现的索引,如果找不到返回-1
stringbuffer.insert(index,string);//在索引为index的位置插入string的内容,原来索引为index的内容自动后移
stringbuffer.length();//字符串长度(2)String类和StringBuffer类互相转换
//String——>StringBuffer
StringBuffer stringBuffer = new StringBuffer(string);
//StringBuffer ->String
//方式一:
String string = stringBuffer.toString();
//方式二: 使用构造器
String string= new String(stringBuffer);4、StringBuilder类
建议优先采用该类,因为在大多数实现中,它比StringBuffer要快。
StringBuilder和StringBuffer均代表可变的字符序列,方法是一样的。
5、Math类
//Math类常用方法:
Math.abs(a);//返回a值的绝对值
Math.cbrt(a);//返回a值的立方根
Math.pow(a,b);//返回a的b次方
Math.sqrt(a);//求a的开方值。比如Math.sqrt(4),返回2
Math.ceil(a);//向上取整,返回>=a的最小整数
Math.floor(a);//向下取整,返回<=a的最小整数
Math.round(a);//对a进行四舍五入处理,返回一个整数
Math.random();//返回[0,1)之间的一个随机小数
Math.max(a,b);
Math.min(a,b);6、Arrays类
//Arrays类常用方法:
Arrays.toString(array);//返回数组的字符串形式
Arrays.sort(array);//把数组按升序排列,数组类型可以是int,char,double...
Arrays.binarySearch(array,element);//array数组已排好序,按二分搜索法查找元素element,找到就返回元素下标
Arrays.fill(array,number);//将指定的number值分配给指定的array数组中的每个元素
Arrays.equals(array1,array2);//比较两个数组内容是否完全一致,返回boolean值
Arrays.asList(num1,num2,num3);//将一组值转换成list链表
Arrays.compare(a,b);//比较大小,返回return b-a;7、System类
//System类常用方法
System.exit(0);//程序退出,0表示退出状态为正常状态
System.arraycopy(src,startIndex,dest,insertIndex,length);//复制数组元素,适合底层调用
//从源数组src下标为startIndex的位置拷贝长度为length的数据到目标数组dest下标为insertIndex的地方
System.currentTimeMillis();//返回当前时间距离 1970-1-1 的毫秒数
System.gc();//运行垃圾回收机制8、BigInteger类
//应用场景:适合保存比较大的整型数据
//应用原则:long不够用时就用BigInteger
//常用方法:加减乘除
BigInteger b1=new BigInteger("9999999999999999999999999999999999999999");
BigInteger b2=new BigInteger("1111111111111111111111111111111111111111");
BigInteger add=b1.add(b2);//b1加b2
BigInteger subtract=b1.subtract(b2);//b1减b2
BigInteger multiply=b1.multiply(b2);//b1乘b2
BigInteger divide=b1.divide(b2);//b1除b2
9、BigDecimal类
//应用场景:适合保存精度很高的数据
//应用原则:double不够用时就用BigDecimal
//常用方法:加减乘除
BigDecimal b1=new BigDecimal("9.9999999999999999999999999999999");
BigDecimal b2=new BigDecimal("1.1111111111111111111111111111111");
b1.add(b2);//b1加b2
b1.subtract(b2);//b1减b2
b1.multiply(b2);//b1乘b2
b1.divide(b2, BigDecimal.ROUND_CEILING);//b1除b2
//divide方法可能会抛出异常 ArithmeticException,
//所以要指定精度BigDecimal.ROUND_CEILING。如果有无限循环小数,就会保留分子的精度
10、日期类
第一代日期类
Date d1=new Date();//获取当前系统时间
Date d2=new Date(9234567);//通过指定毫秒数得到时间
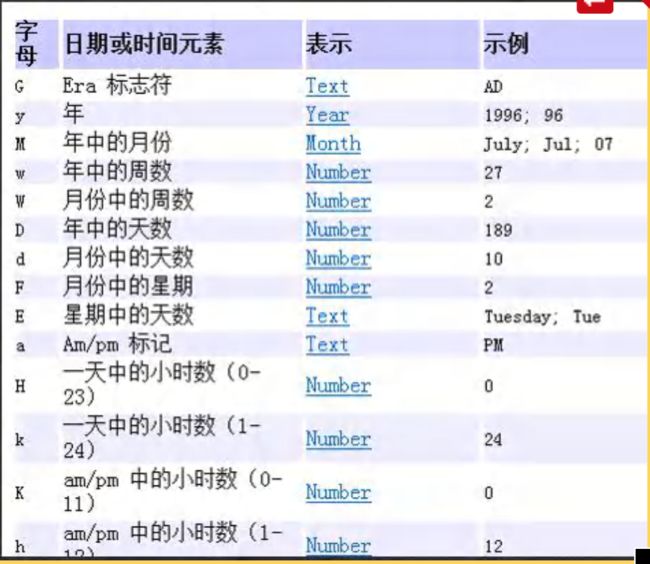
//格式化:日期——》文本
SimpleDateFormat sdf = new SimpleDateFormat("yyyy年MM月 dd日hh:mm:ss E");
String format = sdf.format(d1); //将日期转换成指定格式的字符串
//解析:文本——》日期
String s = "1996年01月01日 10:20:30 星期一";
Date parse = sdf.parse(s);
sdf.format(parse);第二代日期类(Calendar类,获取一些日历片段)
Calendar c = Calendar.getInstance(); //创建日历类对象
System.out.println("月:" + (c.get(Calendar.MONTH) + 1));//月份从0开始算
System.out.println("日:" + c.get(Calendar.DAY_OF_MONTH));
System.out.println("小时:" + c.get(Calendar.HOUR));
System.out.println("分钟:" + c.get(Calendar.MINUTE));
System.out.println("秒:" + c.get(Calendar.SECOND));
//格式化,自由组合,没有专门格式化的方法
System.out.println(c.get(Calendar.YEAR) + "-" + (c.get(Calendar.MONTH) + 1) + "-" + c.get(Calendar.DAY_OF_MONTH) + " " +
c.get(Calendar.HOUR_OF_DAY) + ":" + c.get(Calendar.MINUTE) + ":" + c.get(Calendar.SECOND) );第三代日期类
LocalDateTime ldt = LocalDateTime.now(); //返回表示当前日期时间的对象
LocalDate now = LocalDate.now(); //获取年月日
LocalTime now2 = LocalTime.now();//获取时分秒
DateTimeFormatter dateTimeFormatter = DateTimeFormatter.ofPattern("yyyy-MM-dd HH:mm:ss");//使用 DateTimeFormatter 对象来进行格式化
String format = dateTimeFormatter.format(ldt);
System.out.println("年=" + ldt.getYear());
System.out.println("月=" + ldt.getMonth());
System.out.println("月=" + ldt.getMonthValue());
System.out.println("日=" + ldt.getDayOfMonth());
System.out.println("时=" + ldt.getHour());
System.out.println("分=" + ldt.getMinute());
System.out.println("秒=" + ldt.getSecond());
LocalDateTime localDateTime = ldt.plusDays(890);
System.out.println("890天后的日期" + dateTimeFormatter.format(localDateTime));
LocalDateTime localDateTime2 = ldt.minusMinutes(3456);
System.out.println("3456分钟前的日期" + dateTimeFormatter.format(localDateTime2));Instant now = Instant.now();//获取表示当前时间戳的对象
Date date = Date.from(now);//把 Instant 转成 Date
Instant instant = date.toInstant();//把 date 转成 Instant 对象Collections类
- Collections是一个操作Collection集合和Map集合的工具类
- Collection是一个接口,而Collections是一个静态方法的集合类,它在java.until包下
//Collections常用方法
List list=new ArrayList<>();
Collections.sort(list);//对集合list中的内容从小到大进行排序(经测试数字,字母都可以)
Collections.reverse(list);//对集合list中的内容按原顺序倒序排列
Collections.shuffle(list);//对集合list中的内容随机进行排序
Collections.swap(List list,int i,int j);//交换集合list中指定索引位置的元素
Collections.fill(List list,Object o);//用对象o替换集合list里的所有元素
Collections.copy(List list,List list2);//将集合list2中的元素全部复制到list中,并且覆盖相应索引的元素
Collection.min(list);//找出集合list中的最小元素
Collection.max(list);//找出集合list中的最大元素附:
时间复杂度
空间复杂度