C++递推基本概念和基础知识
目录
一、递推的概念
什么是递推算法?
解决递推问题的一般形式
二、递推和递归的区别
三、递推的实例
一、递推的概念
什么是递推算法?
“递推”是计算机解题的一种常用方法。利用“递推法”解题首先要分析归纳出“递推关系”。如经典的斐波那契数列问题,用 f (i)表示第 i 项的值,则 f (1) =0,f(2) =1,在 n>2 时,存在递推关系:f (n) = f(n-1) + f(n-2)。
在递推问题模型中,每个数据项都与它前面的若干个数据项(或后面的若干个数据项)存在一定的关联,这种关联一般是通过一个“递推关系式”来描述的。求解问题时,需要从初始的一个或若干数据项出发,通过递推关系式逐步推进,从而推导计算出最终结果。这种求解问题的方法叫“递推法”。其中,初始的若干数据项称为“递推边界”。
解决递推问题的一般形式
- 建立递推关系式
- 确定边界条件(即初始值)
- 递推求解
二、递推和递归的区别
- 从程序上看,递归表现为自己调用自己,递推则没有这样的形式。
- 递归是从问题的最终目标出发,逐渐将复杂问题化为简单问题,最终求得问题是逆向的。递推是从简单问题出发,一步步的向前发展,最终求得问题。是正向的。
- 递归中,问题的n要求是计算之前就知道的,而递推可以在计算中确定,不要求计算前就知道n。
- 一般来说,递推的效率高于递归(当然是递推可以计算的情况下)
三、递推的实例
1.超级楼梯
Description
有一个超级楼梯共N级,刚开始时你在第一级,若每次只能跨上一级或两级,要走上第N级,共有多少种走法?
其中N(1 <= N <= 105)。Input
输入一个整数N
Output
输出走到第N级的方案数,答案可能会很大,结果模上2333333。
Sample Input
3
Sample Output
2
这个题是比较典型的递推。可以慢慢分析一下,对于n级台阶,假设有f[n]种走法,如果最后一步走1级那么剩下n-1级自然有f[n-1]种走法;如果最后一步走2级那么剩下n-2级就有f[n-2]种走法。总结出这个公式:
![]()
故代码如下:
#include
#include
int main(){
int i,j,n,a,f[100];
scanf("%d",&n);
for(i=0;i 2.一只小蜜蜂
Description
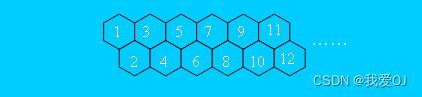
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中,蜂房的结构如图所示。其中起点为a,终点为b(1 <= a < b <= 105)。
Input
两个整数a和b,表示蜜蜂的起点和终点。
Output
一个整数表示从起点a到达终点b的路线数,答案可能会很大,结果模上2333333。
Sample Input
2 4
Sample Output
2
仔细观察,其实就是上面的斐波那契数列,所以还是这个公式
![]()
#include
typedef long long ll;
using namespace std;
ll f[100000];
int main(){
int n,m;
cin >> n >> m;
f[n] = 1;
f[n + 1] = 1;
f[n + 2] = 2;
for(int i = n + 3;i <= m;i ++){
f[i] = (f[i - 1] + f[i - 2]) % 2333333;
}
cout << f[m];
return false;
} 3.外星母牛的故事
Description
有一头外星母牛,它每年年初生一头外星小母牛。每头外星小母牛从第四个年头开始,每年年初也生一头外星小母牛。
请问在第N (1 <= N <= 105)年的时候,共有多少头外星母牛?(假如外星母牛可以永生)
Input
输入一个整数N。
Output
输出一个整数,表示的N年的外星母牛总数,答案可能会很大,结果模上2333333。
Sample Input
6
Sample Output
9
本题明显可用递推来解决,从第五年开始,有其他的母牛开始生子,所以递推从5开始,每年的母牛总数就是上一年的母牛数目+新生母牛数,若用f[i]表示第i年母牛总数,则有![]()
注意母牛在第4个年头生子,所以新生母牛数目应该是f[i-3],也就是i-3那年的母牛总数。
#include
typedef long long ll;
using namespace std;
ll f[100000];
int tmp = 2;
int main(){
int m;
cin >> m;
f[1] = 1;
f[2] = 2;
f[3] = 3;
f[4] = 4;
f[5] = 6;
for(int i = 6;i <= m;i ++){
f[i] = (f[i - 1] + f[i - 3]) % 2333333;
//cout << f[i] << endl;
}
cout << f[m];
return false;
} 4.铺地板I
Description
有一个大小是 2 x N(1 <= N <= 105)的网格,现在需要用2种规格的骨牌铺满,骨牌规格分别是 2 x 1 和 2 x 2,请计算一共有多少种铺设的方法。
Input
输入一个整数N,表示是一个2 * N的网格。
Output
输出一个整数,表示最终的铺设方案数,答案可能会很大,结果模上2333333。
Sample Input
1
Sample Output
1
可以使用动态规划来解决这个问题。设f[i]表示2 x i网格的铺设方案数,注意到最后一列可能由1个2 x 1的骨牌或者1个2 x 2的骨牌组成。如果最后一列是2 x 1的骨牌,则前面的列可以任意铺设,此时方案数为f[i-1]。如果最后一列是2 x 2的骨牌,则倒数第二列也必须是2 x 2的骨牌,前面的列可以任意铺设,此时方案数为f[i-2]。
因此有递推式:![]()
边界条件f[1] = 1,f[2] = 2
注意:最后答案要取模2333333
#include
typedef long long ll;
using namespace std;
ll f[100005];
int main(){
ll m;
cin >> m;
f[1] = 1;
f[2] = 3;
for(ll i = 3;i <= m;i ++){
f[i] = (f[i - 1] + 2 * f[i - 2]) % 2333333;
//cout << f[i] << endl;
}
cout << f[m];
return false;
} 5.[NOIP2002]过河卒 T4
Description
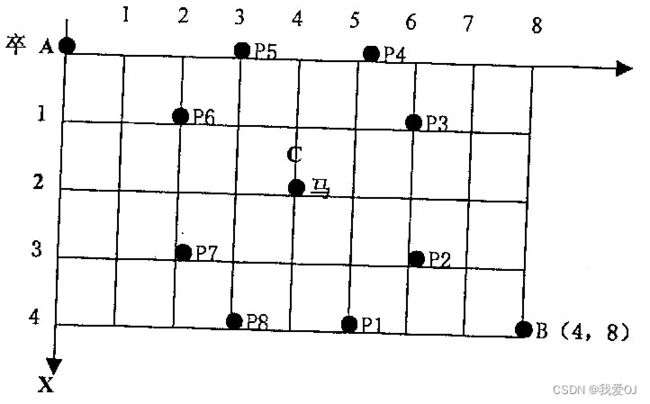
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C<>A,同时C<>B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
Input
B点的坐标(n,m)以及对方马的坐标(X,Y)
Output
一个整数(路径的条数)。
Sample Input
6 6 3 2
Sample Output
17
我们定义状态dp[][]为卒子走到坐标(i,j)时能走的条数
如果不考虑马的控制,i,j) 点的路径条数等于它上面和左边的路径条数之和,即
![]()
我们这道题中要考虑马的位置,当卒子走到马的控制点时,我们跳过这个点,让这个点还为0,不会影响控制点下边和左边的dp[][],这样我们就可以继续计算其他点的dp[][]的值了。
#include
#define maxn 110
using namespace std;
int main()
{
bool b[maxn][maxn];
long long a[maxn][maxn];
memset(b,0,sizeof(b));
int dx[8]={2,1,-1,-2,-2,-1,1,2};
int dy[8]={1,2,2,1,-1,-2,-2,-1};
int n,m,x,y;
cin>>n>>m>>x>>y;
b[x][y]=1;
for(int i=0;i<=7;i++)
if(x+dx[i]>=0&&x+dx[i]<=n&&y+dy[i]>=0&&y+dy[i]<=m)
b[x+dx[i]][y+dy[i]]=1;
int k=0;
while(!b[k][0]&&k<=n)
{
a[k++][0]=1;
}
int l=0;
while(!b[0][l]&&l<=m)
{
a[0][l++]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(b[i][j]) a[i][j]=0;
else {a[i][j]=a[i-1][j]+a[i][j-1];
a[i][j]=a[i-1][j]+a[i][j-1];}
cout<