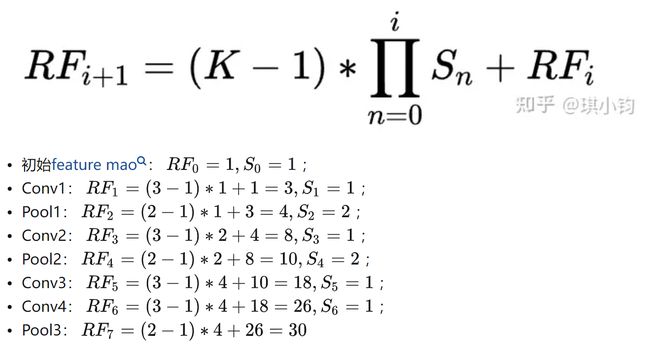优化器的作用是什么？例举一下神经网络中常用的优化器？
优化器作用：求出让损失函数最小化的参数。
常用优化器：
1、Adam
关联所有样本的梯度，便于求解全局最优解，始终含有前面梯度的信息，把前面的梯度传到后面
优点：自动调节学习率， 速度快， 梯度传导
2、梯度下降SGD
批量梯度下降：用所有的样本更新参数，计算量大
随机梯度下降：每看一个数据更新参数，更准确，但是计算量大
小批量随机下降：按批来更新参数，前两者的折中
缺点：(1)训练速度慢(2)容易陷入局部最优
什么是感受野，感受野如何计算？
一、感受野的概念
感受野(Receptive Field)的定义：卷积神经网络每一层输出的特征图(feature map)上的像素点映射回输入图像上的区域大小。通俗点的解释是，特征图上一点，相对于原图的大小，也是卷积神经网络特征所能看到输入图像的区域。
二、举例说明
(1)若输入图像的尺寸大小是55，经过两次33的卷积核(其中stride=1,padding=0)后，其感受野大小为5*5，如下图所示：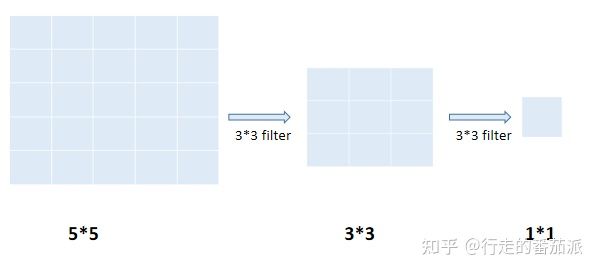
(由卷积计算公式：N=(W-F+2P)/S+1，得到第一次卷积后的图像大小为33，第二次卷积后的图像大小为11)
(2)若输入图像的尺寸大小是77，经过三次33的卷积核(其中stride=1,padding=0)后，其感受野大小为7*7，如下图所示：
(由卷积计算公式：N=(W-F+2P)/S+1，得到第一次卷积后的图像大小为55，第二次卷积后的图像大小为33，第三次卷积后的图像大小为1*1)
也就是说，随着卷积核的增多(即网络的加深)，感受野会越来越大。
三、感受野的计算
1. 从后往前：即先计算最深层在前一层上的感受野，然后以此类推逐层传递到第一层。
(1)计算公式：
其中\(RF_i\)， 表示 \(i\) 层感受野大小， \(i\)表示当前特征层的层数， \(stirde\)是卷积的步长， \(K_{sizei}\)是本层卷积核的大小。
(2)注意：
1、感受野大小的计算不考虑padding的大小；
2、最后一层的特征图感受野的大小等于其卷积核的大小，即每个输出特征RF=(1-1)* S + K = K；
3、第i层特征图的感受野大小和第i层的卷积核大小和步长有关系，同时也与第(i+1)层特征图的感受野大小有关。
(3)例子：
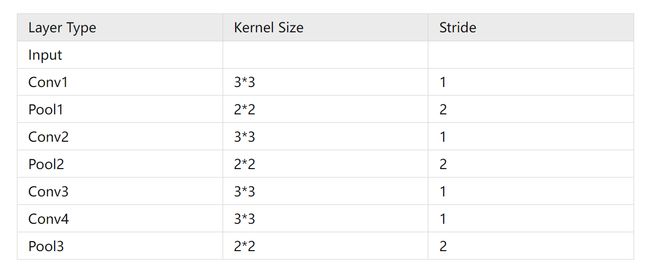
从最后一层的Pool3池化层开始计算感受野：
pool3：RF=2(最后一层池化层输出特征图的感受野大小等于卷积核的大小)
conv4：RF=(2-1)*1+3=4
conv3：RF=(4-1)*1+3=6
pool2：RF=(6-1)*2+2=12
conv2：RF=(12-1)*1+3=14
pool1：RF=(14-1)*2+2=28
conv1：RF=(28-1)*1+3=30
因此，pool3输出的特征图在输入图片上的感受野为30*30。2. 从前往后：从初始图像开始，按照网络的前向传播过程，从前往后一层层计算每层的感受野。
(1)计算公式：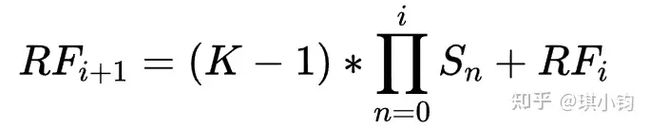
其中：
- \(RF_{i+1}\)表示当前层感受野
- \(RF_i\)表示上一层感受野
- K 表示当前层核大小
- \(S_n\)表示前面几层的步长之积
规定：
- 初始feature map的感受野为1，即\(RF_i=1\)。
- 初始s=1。
(2)例子：
四、感受野的应用
1、小尺寸的卷积代替大尺寸的卷积，可减少网络参数、增加网络深度、扩大感受野(例如：3 个 3 x 3 的卷积层的叠加可以替代7*7的卷积)，网络深度越深感受野越大性能越好；
为什么两个3x3卷积等于一个5x5卷积呢？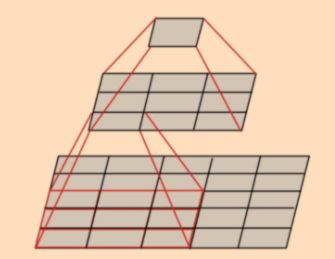
因为他们感受野相同。
这样做有什么好处呢？
1、增加网络层数，层之间可以加入激活函数，增加了网络的非线性表达能力。
2、参数更少，2个3x3的卷积核有18个参数，1个5x5的卷积核有25个参数。2、对于分类任务来说，最后一层特征图的感受野大小要大于等于输入图像大小，否则分类性能会不理想；
3、对于目标检测任务来说，若感受野很小，目标尺寸很大，或者目标尺寸很小，感受野很大，模型收敛困难，会严重影响检测性能；所以一般检测网络anchor的大小的获取都要依赖不同层的特征图，因为不同层次的特征图，其感受野大小不同，这样检测网络才会适应不同尺寸的目标。
卷积、池化输出大小如何计算？
(H,W)的特征图卷积后的大小如何计算:
假设卷积核大小是(f,f)，步长是s，填充是p，那么卷积后:
(H,W)的特征图池化后的大小如何计算:
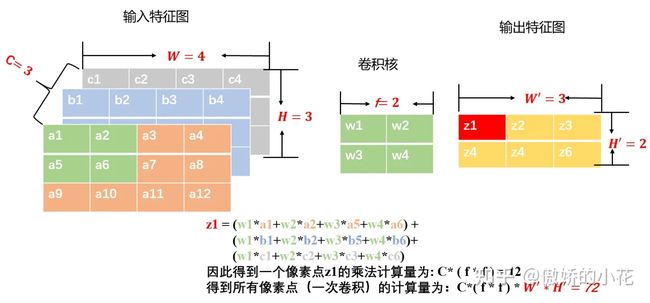
一次卷积的计算量是多少？
假设输入是(H,W,C)，使用一个size为(f,f)的卷积核，卷积后的输出特征图size为(H',W')，则乘法计算量为：
具体分析可看图1。
如果使用C'个不同的卷积核，则卷积后的输出特征图的size为：(H',W',C')，那么一次卷积的计算量为：