CSI指纹预处理（中值、均值、Hampel、维纳滤波、状态统计滤波器）

目录

前言

1、箱线法

2、中值滤波器

3、均值滤波器

4、Hampel滤波器

5、维纳滤波

6、状态统计滤波器

---

前言

因为设备、温度和实验室物品摆设等因素的影响，未经处理的CSI数据不能直接使用，需要对数据进行异常值处理以保证数据的稳定性，同时减少环境中人的活动、突发性干扰对CSI的影响，下面将简单探讨MATLAB自带的几种滤波器对CSI幅值数据的处理，一些升级版的滤波程序由你们自主思考。

1、箱线法

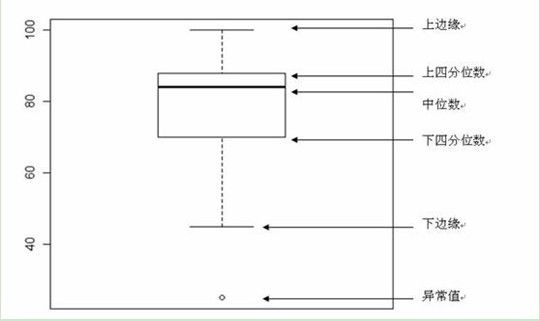
箱线法主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较，我们可以先使用箱线法可视化异常值，下面给出了箱线法可视化异常值及箱线法对照图，感兴趣的可以自己去了解一下。

  图1 箱线法可视化异常值

  图2 箱线法对照图 

2、中值滤波器

中值滤波是一种非线性滤波方法，可以有效去除信号中的噪声，同时保留信号中的边缘信息。中值滤波的基本思想是将信号中每个采样点的值替换为该点周围一定范围内的中值。

MATLAB中可以使用medfilt1函数对信号进行中值滤波。该函数的语法为：

y = medfilt1(x, w)

x表示我们要处理的数据；w表示均值滤波器的窗口大小，y表示滤波后的结果。

load('raw_amp');
best_amp= medfilt1(raw_amp, 5);
figure(1)
plot(raw_amp);
title('原始幅值');
ylabel('幅值');
figure(2)
plot(best_amp);
title('中值滤波');
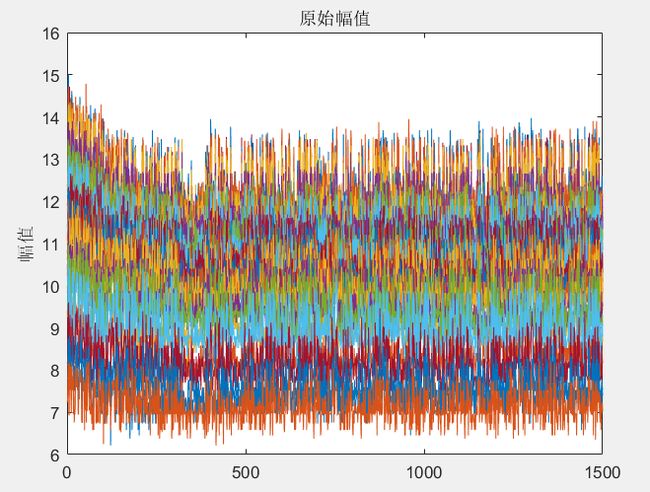
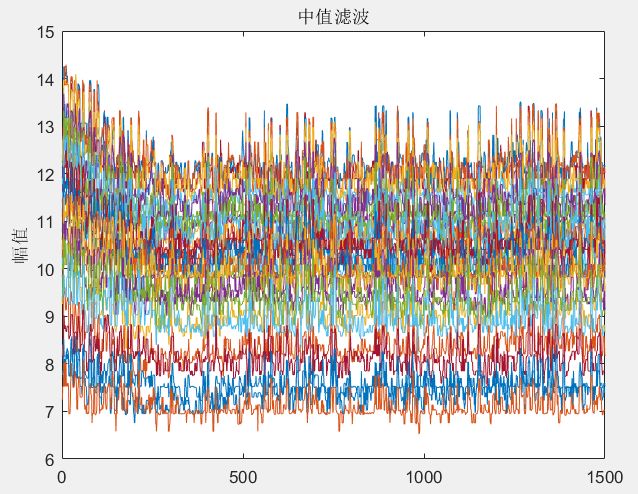
ylabel('幅值');

中值滤波处理前后的幅值图像：

 图3 中值滤波处理前

  图4 中值滤波处理后

3、均值滤波器

均值滤波是一种线性滤波方法，可以用于平滑信号，去除噪声。均值滤波的基本思想是将每个采样点的值替换为该点周围一定范围内的平均值。

MATLAB中可以使用smoothdata函数对信号进行均值滤波。该函数的语法为：

y = smoothdata(x, 'movmean', w)

 x表示我们要处理的数据；w表示均值滤波器的窗口大小，y表示滤波后的结果。

best_amp2 = smoothdata(raw_amp, 'movmean', 5);
figure(3)
plot(raw_amp);
title('原始幅值');
ylabel('幅值');
figure(4)
plot(best_amp2);
title('均值滤波');
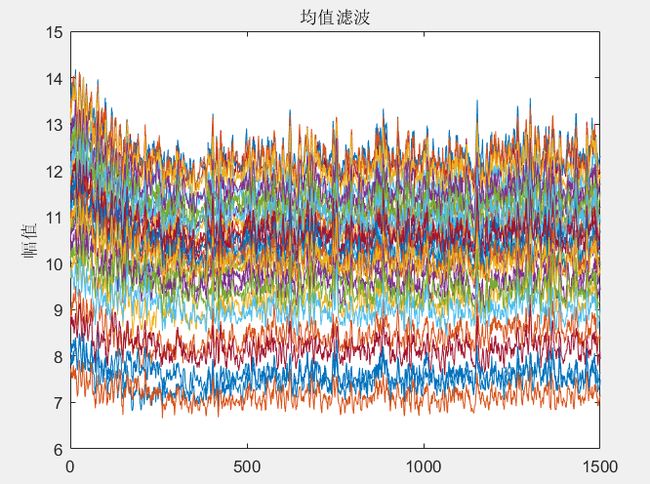
ylabel('幅值');

 均值滤波处理前后的幅值图像：

图5 均值滤波处理前 

图6 均值滤波处理后

4、Hampel滤波器

Hampel滤波是一种基于中位数的离群点检测和滤波方法。它通过对信号进行中位数滤波，并计算每个数据点与中位数之间的距离来识别离群点。如果距离大于某个阈值，则该数据点被视为离群点，并用中位数替换。该方法具有抗噪声能力和对离群点的较好识别能力。它常用于数据清洗、异常检测和信号预处理。

MATLAB中可以使用hampel函数对信号进行滤波。该函数的语法为： 

y=hampel(x,k,nsigma)

x表示我们要处理的数据；k表示可指定窗口中每个样本周围的样本数，默认为3；nsigma表示指定几倍的标准差；y表示滤波后的结果。 

great_data = hampel(raw_amp,5,2);
figure(5)
plot(1:1:30,raw_amp);
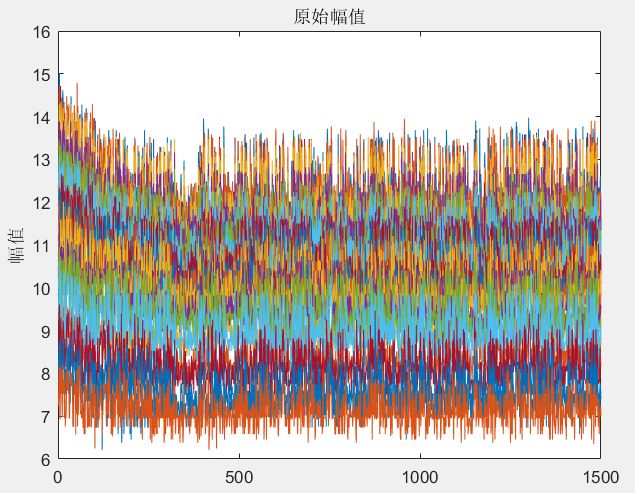
title('原始幅值');
ylabel('幅值');
figure(6)
plot(1:1:30,great_data);
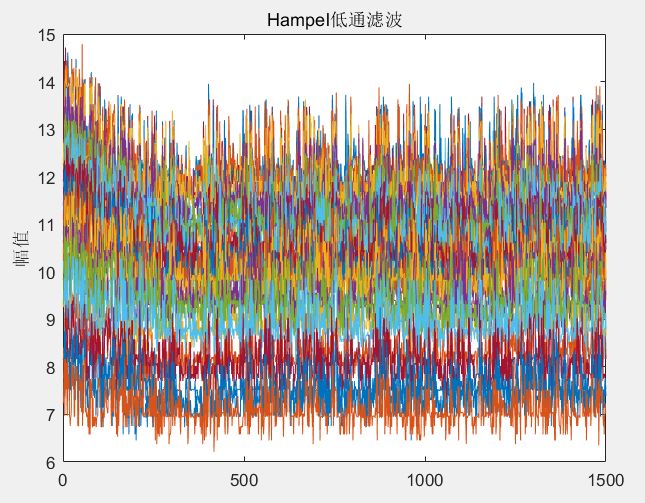
title('Hampel低通滤波');
ylabel('幅值');

 Hampel滤波处理前后的幅值图像：

图7  Hampel滤波处理前  

图8  Hampel滤波处理后  

5、维纳滤波

维纳滤波是一种二维自适应除噪滤波器，根据局部方差来调整滤波器效果。对于去除高斯噪声效果明显。

维纳滤波的两个函数wiener2与deconvwnr都能够完成维纳滤波的功能，但两者具有差异性，感兴趣的可以自己去了解，MATLAB中维纳滤波代码如下：

y=wiener2(x,[m,n]);

x指原始CSI的幅值；y指维纳滤波后的幅值；[m,n]指定滤波器窗口大小为m*n，默认值为3*3。

load('raw_amp');
m=5;
n=5;
best_amp3=wiener2(raw_amp,[m,n]);
figure(7)
plot(raw_amp);
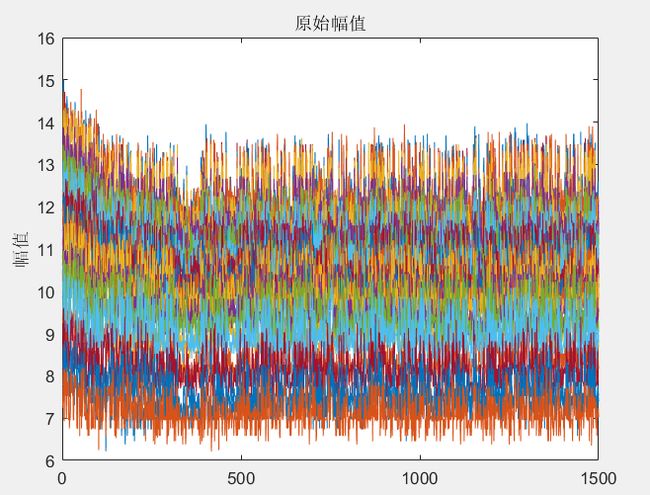
title('原始幅值');
ylabel('幅值');
figure(8)
plot(best_amp3);
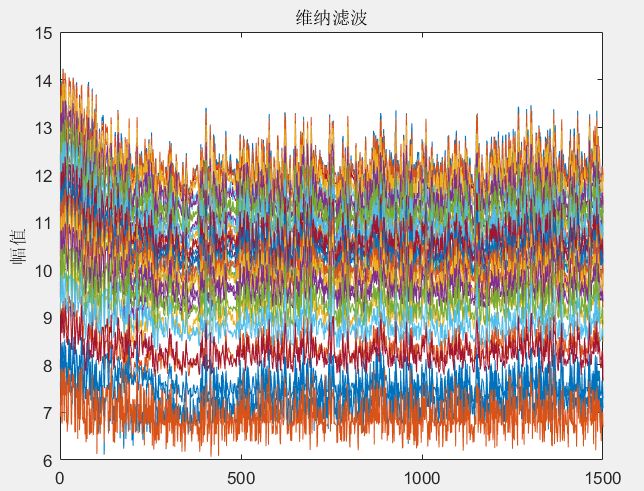
title('维纳滤波');
ylabel('幅值');

  维纳滤波处理前后的幅值图像：

 图9 维纳滤波处理前  

 图10  维纳滤波处理后  

6、状态统计滤波器

它的滤波概念是中值滤波的推广，中值滤波是对于给定的n个数值｛al ,a2,...,an｝，将它们按大小顺序排列，取中间的那个值作为滤波器的输出。而状态统计滤波器将n个非零数值按小到大排序后处于第k个位置的元素作为滤波器的输出。MATLAB中状态统计滤波器可以用ordfilt2函数表示：

y=ordfilt2(x,order,domain);

x指原始CSI的幅值；y指状态统计滤波后的幅值；order 为滤波器输出的顺序值；domain为滤波窗口；

（1）y=ordfilt2(x,13,ones(5,5))，在模板内的像素值都为非零时，相当于模板为5×5的中值滤波(order=13，刚好为窗口的中间值);

（2）y=ordfilt2(x,1,ones(5,5))，在模板内的像素值都为非零时，相当于5×5的最小值滤波(order=1，刚好为窗口的最小值);

（3）y=ordfilt2(x,25,ones(5,5))，在模板内的像素值都为非零时，相当于5×5的最大值滤波(order=25，刚好为窗口的最大值);

load('raw_amp');
order = 10;
domain = ones(5,5);
best_amp4=ordfilt2(raw_amp,order,domain);
figure(8)
plot(raw_amp);
title('原始幅值');
ylabel('幅值');
figure(9)
plot(best_amp4);
title('状态统计滤波器');
ylabel('幅值');

 状态统计滤波器处理前后的幅值图像：

  图11  状态统计滤波器处理前

图12  状态统计滤波器处理后 

CSI的相关文章请参考：CSI数据预处理之卡尔曼滤波、高斯滤波、简单平均_rssi高斯滤波_数产小黑娃的博客-CSDN博客卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。卡尔曼滤波算法在估计值和观测值之间做了一个修正。........................https://blog.csdn.net/qq_53860947/article/details/126175335

室内定位之CSI指纹定位_数产小黑娃的博客-CSDN博客随着WiFi技术的发展，IEEE802.11n系列通信协议及其之后的无线局域网协议应用了多输入多输出（multiple－input multiple－output，MI-MO）和正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）等技术，使得WiFi收发设备之间的信道特征可以在物理层进行估计，并以信道状态信息（channel status information，CSI）的形式存储下来。https://blog.csdn.net/qq_53860947/article/details/126180830