线性二自由度汽车模型的微分方程

Python微信订餐小程序课程视频

https://blog.csdn.net/m0_56069948/article/details/122285951

Python实战量化交易理财系统

https://blog.csdn.net/m0_56069948/article/details/122285941
本部分内容系汽车理论第五章第三节，我做了一点整理和总结。

1. 二自由度

二自由度最开始是指侧向与横摆两个自由度。

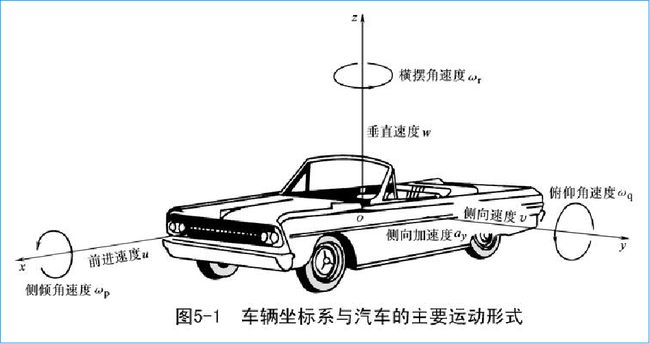
下图是一个车辆坐标系下，车辆存在六个自由度：

• 沿x轴运动，前进运动
• 沿y轴运动，侧向运动
• 沿z轴运动，垂直运动
• 绕x轴转动，侧倾运动
• 绕y轴转动，俯仰运动
• 绕z轴转动，横摆运动

那么，如何将汽车的自由度限制到两个呢？

汽车理论给出了如下假设：

1. 忽略悬架的作用。
   • 汽车车身无法依靠减震器和弹性元件实现沿z轴的运动，无法上下振动。
   • 也没有所谓的独立悬架和非独立悬架之分，无法左右摇动，即绕x轴的侧倾运动。
   • 没有弹性元件也无法完成绕y轴的俯仰运动。
2. 汽车前进速度不变。
   • 也不用考虑沿x轴运动。因为之后汽车理论将用运动学和动力学的方式联立等式（理论力学的内容），而沿x轴速度不变意味着x轴方向的加速度为0，不用参与到联立的等式中。

上面两个假设限定了四个自由度，剩下的就是沿y轴的侧向运动和绕z轴的横摆运动，这就是汽车的二自由度。

2. 两轮汽车模型

下图是经典的简化得到的两轮汽车模型。质心为O，左边的是后轮，距离质心"轴距"为b；右边是前轮，距离质心"轴距"为a。汽车要向左转。

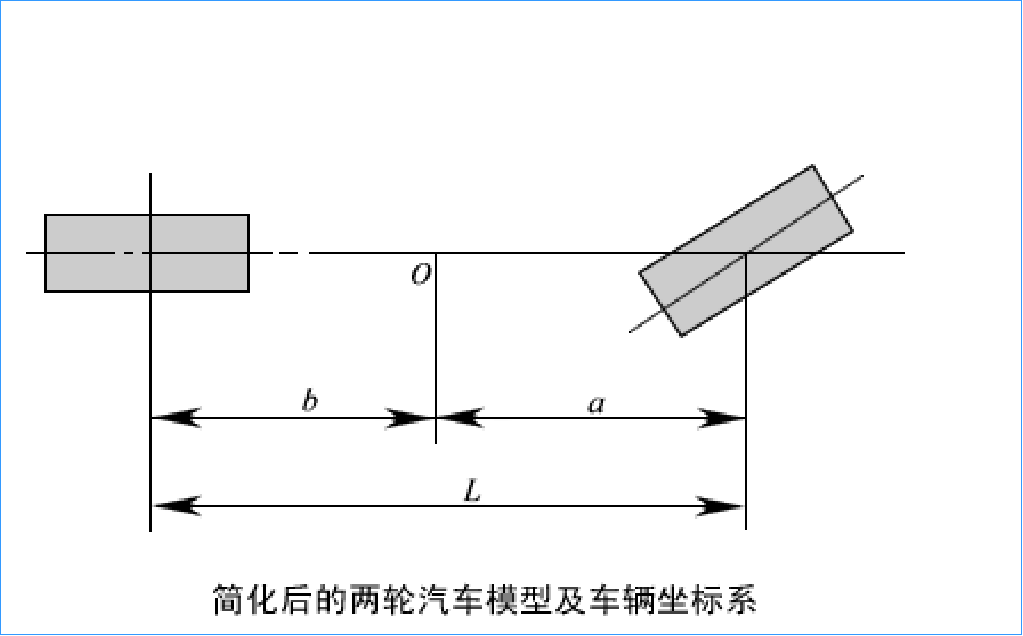
那么，为什么可以简化成下面的模型？主要假设是三条

• 忽略了悬架的作用，那么汽车车身可以看作是只做平行于地面的平面运动。
• 汽车侧向加速度ay≤0.4gay≤0.4ga_y≤0.4g，轮胎侧偏特性处于线性范围内。这一条说明，前(或后)轮的左、右两轮侧偏刚度相等，可以把左右轮压扁看成一个轮子，侧偏刚度是原来一个轮子的两倍。（这里忽略了悬架的作用，所以左右轮的垂直载荷相等，垂直载荷对侧偏刚度有一定影响）
• 不计地面切向力FXFXF_X、外倾侧向力FYγFYγF_{Yγ}、回正力矩 TZTZT_Z、垂直载荷的变化对轮胎侧偏刚度的影响。

3. 运动学分析

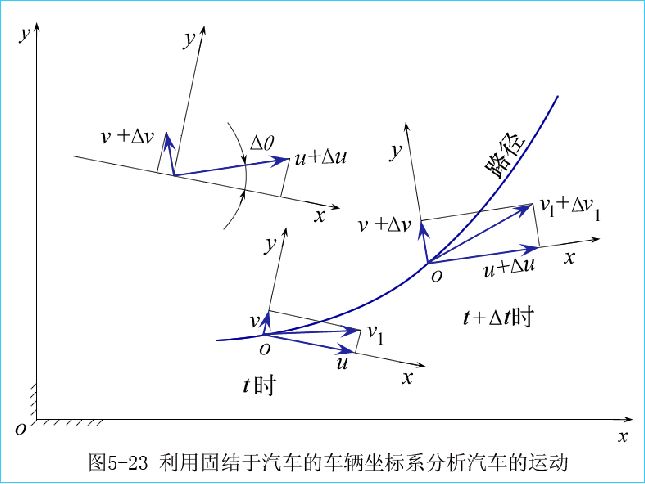
图中三处蓝色线是车辆坐标系，全平面是大地坐标系。右下的两处车辆坐标系是t和t+Δt时刻的，汽车左转，质心向左运动，
左上角的车辆坐标系比较特殊，是用来分析使用的。虚线的x、y坐标轴是t时刻的，蓝色线的速度是t+Δt时刻的。t时刻到t+Δt时刻，沿该坐标系y轴速度分量变化为

(v+Δv)cosΔθ−v+(u+Δu)sinΔθ(v+Δv)cosΔθ−v+(u+Δu)sinΔθ(v+Δv)cosΔ\theta-v+(u+Δu)sinΔ\theta
由于ΔθΔθΔ\theta很小，所以有

cosΔθ≈1,sinΔθ≈Δθ≈0cosΔθ≈1,sinΔθ≈Δθ≈0cosΔ\theta\approx1,
sinΔ\theta\approxΔ\theta\approx0
如果再忽略二阶微量，那么沿该坐标系x轴速度分量变化可以化简为

Δv+uΔθΔv+uΔθΔv+uΔ\theta
上式除以Δt，并且取极限，便是汽车质心绝对加速度在车辆坐标系Oy轴的分量

ay=dvdt+udθdt=v⋅+uwray=dvdt+udθdt=v·+uwra_y=\frac{dv}{dt}+u\frac{d\theta}{dt}=\overset{·}{v}+uw_r
这里的wrwrw_r是横摆角速度。

4. 动力学分析

下图是二自由度汽车模型的俯视图。

下面是对该模型的一些说明：

• δδ\delta是前轮转角(方向盘输入引起的)
• α1α1\alpha_1是前轮的侧偏角，α2α2\alpha_2是后轮的侧偏角
• ξξ\xi是航向角，ξ=δ−αξ=δ−α\xi=\delta-\alpha
• u1u1u_1是前轮速度，u2u2u_2是后轮速度
• FY1FY1F_{Y1}、FY2FY2F_{Y2}是前、后轮的侧偏力，分别垂直于各自的车轮平面
• 点O’是此时两车轮的瞬心，是u1u1u_1和u2u2u_2垂线的交点。
• v1v1v_1是汽车的绝对速度，方向是根据oo’连线所确定的垂线方向
• 质心的侧偏角β=v/uβ=v/u\beta=v/u，vvv是质心沿y轴的速度分量，uuu是质心沿x轴的速度分量

汽车受到的外力沿y轴方向的合力与绕质心的力矩和为：

{∑FY=FY1cosδ+FY2∑MZ=αFY1cosδ−bFY2{∑FY=FY1cosδ+FY2∑MZ=αFY1cosδ−bFY2\begin{cases}
\sum F_Y = F_{Y1}cos\delta + F_{Y2}\
\sum M_Z = \alpha F_{Y1}cos\delta - bF_{Y2}
\end{cases}
考虑到δδ\delta较小，并且有FY1=k1α1FY1=k1α1F_{Y1}=k_1\alpha_1和FY2=k2α2FY2=k2α2F_{Y2}=k_2\alpha_2，所以上面的式子可以写成：

{∑FY=k1α1+k2α2∑MZ=αk1α1−bk2α2{∑FY=k1α1+k2α2∑MZ=αk1α1−bk2α2\begin{cases}
\sum F_Y = k_1\alpha_1+k_2\alpha_2\
\sum M_Z = \alpha k_1\alpha_1- bk_2\alpha_2
\end{cases}
航向角可以近似成前轮速度的正切。v向可以看成是相对于质心的速度矢量加上一个旋转的切向速度(理论力学的内容~)。表达如下式：

ξ≈tanξ=v+awru=β+awruξ≈tanξ=v+awru=β+awru\xi \approx tan\xi = \frac{v+a w_r}{u}=\beta+\frac{a w_r}{u}
于是可以表达前、后轮的侧偏角:

⎧⎩⎨⎪⎪α1=−(δ−ξ)=β+awru−δα2=v−bwru=β−bwru{α1=−(δ−ξ)=β+awru−δα2=v−bwru=β−bwru\begin{cases}
\alpha_1=-(\delta-\xi)=\beta + \dfrac{a w_r}{u}-\delta\
\alpha_2=\dfrac{v-bw_r}{u}=\beta-\dfrac{bw_r}{u}
\end{cases}
由此，可以得到汽车外力、外力矩和汽车运动参数的关系：

⎧⎩⎨⎪⎪⎪⎪∑FY=k1(β+awru−δ)+k2(β−bwru)∑MZ=αk1(β+awru−δ)−bk2(β−bwru){∑FY=k1(β+awru−δ)+k2(β−bwru)∑MZ=αk1(β+awru−δ)−bk2(β−bwru)\begin{cases}
\sum F_Y = k_1(\beta + \dfrac{a w_r}{u}-\delta)+k_2(\beta-\dfrac{bw_r}{u})\
\sum M_Z = \alpha k_1(\beta + \dfrac{a w_r}{u}-\delta)- bk_2(\beta-\dfrac{bw_r}{u})
\end{cases}

5. 运动微分方程

联立运动学和动力学方程，有：

⎧⎩⎨⎪⎪⎪⎪k1(β+awru−δ)+k2(β−bwru)=m(v⋅+uwr)αk1(β+awru−δ)−bk2(β−bwru)=IZwr⋅{k1(β+awru−δ)+k2(β−bwru)=m(v·+uwr)αk1(β+awru−δ)−bk2(β−bwru)=IZwr·\begin{cases}
k_1(\beta + \dfrac{a w_r}{u}-\delta)+k_2(\beta-\dfrac{bw_r}{u})=m(\overset{·}{v}+uw_r)\
\alpha k_1(\beta + \dfrac{a w_r}{u}-\delta)- bk_2(\beta-\dfrac{bw_r}{u})=I_Z\overset{·}{w_r}
\end{cases}
其中IZIZI_Z为汽车绕z轴的转动惯量，wr⋅wr·\overset{·}{w_r}为汽车横摆角加速度。

整理可得二自由度汽车运动微分方程式：

⎧⎩⎨⎪⎪⎪⎪(k1+k2)β+1u(ak1−bk2)wr−k1δm(v⋅+uwr)(ak1−bk2)β+1u(a2k1+b2k2)wr−ak1δ=IZwr⋅{(k1+k2)β+1u(ak1−bk2)wr−k1δm(v·+uwr)(ak1−bk2)β+1u(a2k1+b2k2)wr−ak1δ=IZwr·\begin{cases}
(k_1+k_2)\beta+\dfrac{1}{u}(ak_1-bk_2)w_r-k_1\delta==m(\overset{·}{v}+uw_r)\
(ak_1-bk_2)\beta+\dfrac{1}{u}(a^2k_1+b2k_2)w_r-ak_1\delta=I_Z\overset{·}{w_r}
\end{cases}
该联立的方程式，包含了汽质量和轮胎侧偏刚度两方面的参数，能反映汽车运动曲线的基本特征。