冈萨雷斯DIP第3章知识点

3.1 背景

空间域处理主要分为两类：灰度变换、空间滤波

1. 灰度变换 ：对图像的各个像素进行操作，如：对比度处理和图像阈值处理

2. 空间滤波 ：对图像中每个像素的邻域进行操作 如：图像平滑 和 锐化 。

3.2 一些基本的灰度变换函数

灰度变换是所有图像处理技术中最简单的一种技术 。 由于正在处理的是数字量，所以灰度变换函数的值通常存储在一个表中 且从 $r$ 到 $s$ 的映射是通过 查找表 实现的 。

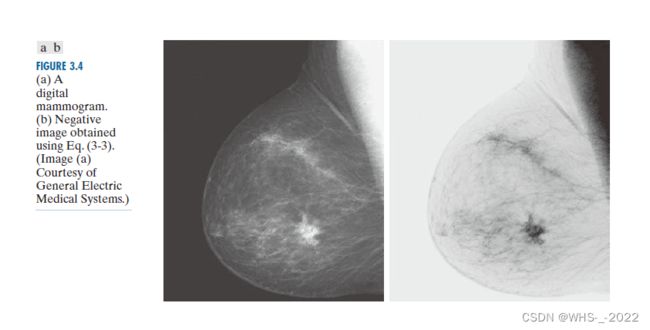
3.2.1 图像反转

可用于增强图像暗色区域中的白色或灰色细节 暗色区域的尺寸很大时 增强效果更好。

$$s=L-1-r$$

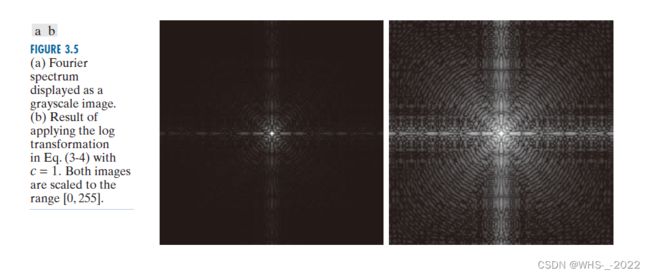
3.2.2 对数变换

$$s=c\log (1+r)$$

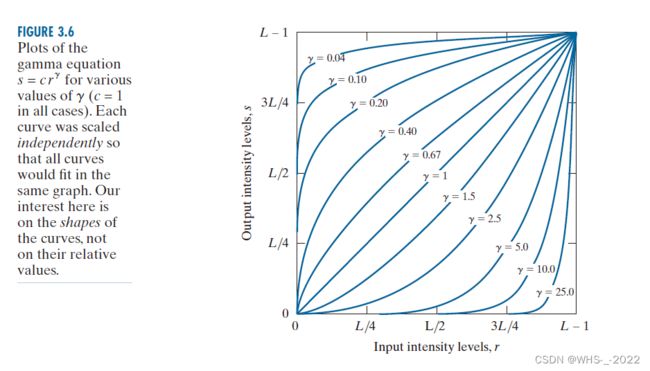
3.2.3 幂律伽马变换

比对数变换更适用于图像灰度级的扩展压缩。

$$s=c{r}^{\gamma }$$

3.2.4 分段线性变换函数

---

3.3 直方图处理

3.3.1 直方图均衡化

$$s_k=T\left(r_k\right)=(L-1)\sum _{j=0}^k{p}_r\left(r_j\right),k=0,1,2,\cdots ,L-1$$

变换(映射) $T(r_k)$ 称为直方图均衡化或直方图线性化变换。

灰度值覆盖整个灰度级的会使得图片对比度增强，更加清晰。刚才推导的方法会产生具有这种分布趋势的灰度，并且具有全自动的优点。

3.3.2 直方图匹配（规定化）

直方图匹配（规定化 )：用于生成具有 规定直方图 的图像的方法 。

3.3.3 局部直方图处理

目的：增强图像中小区域的细节。解决方法：设计基于像素邻域的灰度分布的变换函数 。

3.3.4 使用直方图统计量增强图像

局部均值是邻域中的平均灰度的测度，局部方差(或标准差)是邻域中的灰度对比度的测度。

---

3.4 空间滤波基础

3.4.1 线性空间滤波的原理

空间滤波器在图像 $f$ 和空间滤波器核之间执行乘积之和运算。核是一个阵列，其大小定义了运算的邻域，其系数决定了该滤波器的性质。

一般来说，大小为 $m\times n$ 的核对大小为 $M\times N$ 的图像的线性空间滤波可表示为：

$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$

3.4.2 空间相关与卷积

空间卷积：与空间相关的原理相同，只是把相关运算的核旋转了 $180^{\circ }$。当核的值关于其中心对称时，相关和卷积得到的结果相同。

3.4.3 可分离滤波器核

大小为 $M\times N$ 的图像和大小为 $m\times n$ 的核进行卷积运算，使用可分离核相对于使用不可分离核的计算优势定义为：
$$C=\frac{MNmn}{MN(m+n)}=\frac{mm}{m+n}$$

3.4.4 空间域滤波和频率域滤波的一些重要比较

(1) 卷积是空间域滤波的基础，它等效于频率域中的乘法，反之亦然。

(2) 空间域中振幅为 $A$ 的冲激，是频率域中值为 $A$ 的一个常数，反之亦然。

线性滤波就是找到合适的方法来修改图像的频率内容 。 在 空间域 中 通过 卷积滤波 来实现；在 频率域 中 则是用 乘法滤波器 来实现 。 后者是一种更直观的方法。

---

3.5 平滑（低通）空间滤波器

3.5.1 盒式滤波器核

是最简单的可分离低通滤波器核其系数的值相同 通常为 1 ，归一化常数为 $1/mn$。

适用于所有低通核的这个归一化有两个目的： （1）一个恒定灰度区域的 灰度平均值 将等于 滤波后图像的灰度值 （2）防止在滤波过程中引入偏差 。

3.5.2 低通高斯滤波器核

盒式滤波器对透镜模糊特性的近似能力较差；往往会沿 perpendicular 方向模糊图像。

应用中所选的核通常是圆对称的(也称各向同性，这意味着它们的响应与方向无关)。已证明，高斯核

$$w(s,t)=G(s,t)=K{e}^{-\frac{s^2+t^2}{2{\sigma }^2}}$$

是唯一可分离的圆对称核。

3.5.3 统计排序 非线性 滤波器

中值滤波器：用中心像素的 邻域内的灰度值的中值 在中值计算中包括中心像素的值 代替中心像素的值。

---

3.6 锐化（高通）空间滤波器

3.6.2 使用 二阶导数 锐化图像 拉普拉斯

两个变量的离散拉普拉斯是：

$${\nabla }^{2}f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$$

使用拉普拉斯锐化图像的基本方法是：

$$g(x,y)=f(x,y)+c\left[{\nabla }^{2}f(x,y)\right]$$

3.6.3 钝化掩蔽（unsharp masking）和高提升滤波

从原图像中减去一幅钝化(平滑后的)图像，是20世纪30年代以来印刷和出版业一直用来锐化图像的过程。该过程称为钝化掩蔽，由如下步骤组成：

令 $\bar{f}(x,y)$ 表示模糊后的图像，公式形式的模板为：

$$g_{\text{mask }}(x,y)=f(x,y)-\bar{f}(x,y)$$

然后，将加权后的模板与原图像相加：

$$g(x,y)=f(x,y)+k{g}_{\text{mask }}(x,y)$$

• 当 $k=1$ 时，即为钝化掩蔽；
• 当 $k>1$ 时，即为高提升滤波；

3.6.4 使用一阶导数锐化图像—梯度

图像 $f$ 在坐标 $(x,y)$ 处的梯度(向量; 线性算子, 不是各向同性; 指出了在位置 $(x,y)$ 处 $f$ 的最大变化率的方向)定义为二维列向量：

∇ f = grad ⁡ ( f ) = [ g x g y ] = [ ∂ f ∂ x ∂ f ∂ y ] \nabla f=\operatorname{grad}(f)=\left[\begin{array}{l} g_{x} \\ g_{y} \end{array}\right]=\left[\begin{array}{l} \frac{\partial f}{\partial x} \\ \\ \frac{\partial f}{\partial y} \end{array}\right] ∇f=grad(f)=[gx​gy​​]= ​∂x∂f​∂y∂f​​ ​

向量 $\nabla f$ 的幅度(长度; 不是线性算子, 是各向同性)表示为 $M(x,y)$：
$$M(x,y)=\mathrm{mag}(\nabla f)=\sqrt{g_x^2+g_y^2}$$

在某些实现中， 用绝对值来近似平方运算和平方根运算更适合：

$$M(x,y)\approx \left|g_x\right|+\left|g_y\right|$$

---

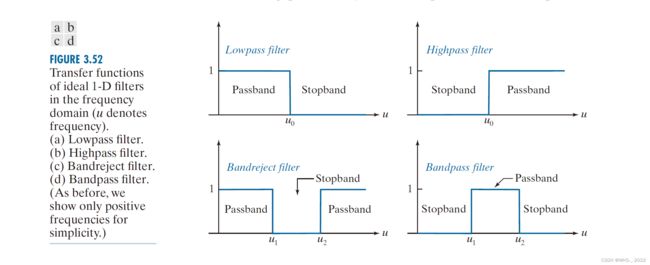
3.7 低通、高通、带阻和带通滤波器

所有传递函数都可由一个低通滤波器传递函数得到。

---

3.39

拉普拉斯核是各向同性（旋转不变的），下面我们来证明一下，可能需要一点高数的知识。

对于没有旋转的坐标，拉普拉斯核定义为：

$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

旋转的坐标，拉普拉斯核定义为：

$${\nabla }^{\prime 2}f=\frac{{\partial }^{2}f}{\partial x^{\prime 2}}+\frac{{\partial }^{2}f}{\partial y^{\prime 2}}$$

旋转 $\theta$ 角度的图像坐标定义为

$$\begin{array}{rl}{x}^{\prime }& =x\cos \theta -y\sin \theta \\ y^{\prime }& =x\sin \theta +y\cos \theta \end{array}$$

一阶偏导为：

$$\begin{array}{rl}\frac{\partial f}{\partial x}& =\frac{\partial f}{\partial x^{\prime }}\frac{\partial x^{\prime }}{\partial x}+\frac{\partial f}{\partial y^{\prime }}\frac{\partial y^{\prime }}{\partial y}\\ & =\frac{\partial f}{\partial x^{\prime }}\cos \theta +\frac{\partial f}{\partial y^{\prime }}\sin \theta \end{array}$$

二阶偏导为：

$$\frac{{\partial }^{2}f}{\partial x^2}=\frac{{\partial }^{2}f}{\partial x^{\prime 2}}{\cos }^2\theta +\frac{\partial }{\partial x^{\prime }}\left(\frac{\partial f}{\partial y^{\prime }}\right)\sin \theta \cos \theta +\frac{\partial }{\partial y^{\prime }}\left(\frac{\partial f}{\partial x^{\prime }}\right)\cos \theta \sin \theta +\frac{{\partial }^{2}f}{\partial y^{\prime 2}}{\sin }^2\theta$$

对 $y$ 的偏导在这里忽略了，最后可以推导出来两个坐标上的拉普拉斯核是各向同性的

$$\begin{array}{rl}\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}& =\frac{{\partial }^{2}f}{\partial x^{\prime 2}}\left[{\cos }^2\theta +{\sin }^2\theta \right]+\frac{{\partial }^{2}f}{\partial y^{\prime 2}}\left[{\sin }^2\theta +{\cos }^2\theta \right]\\ & =\frac{{\partial }^{2}f}{\partial x^{\prime 2}}+\frac{{\partial }^{2}f}{\partial y^{\prime 2}}\end{array}$$