离散化以及树状数组

今天我们先来讲一讲什么叫做离散化（简单的映射关系）

一、离散化

一、概念：就是把一个无限的空间去映射到一个有限的空间中去（通俗的可以理解成将数据相应的缩小）为了更好的理解，请看下图：

       已知A和B两条直线，你觉得两条直线是否长度相等？ 我们无论是肉眼看还是拿比较紧密的尺子进行测量，A和B的长度永远不可能相等，但是在某一方面，它们的长度是相等的，看下图：

      以直线A和直线B做一个三角形，假设有两条直线相交与A和B，在A和B中分别相交与点m n和点m' n',由此可知，我们都可以在直线B上找到与A中的点一一对应的点， 所以我们可以理解成A线段中点作成集合和B线段中点作成集合相等，所以我们理解成A和B的长度相等，所以这就是映射，想必大家已经对映射有了最基本的概念，下面我们来讲解什么是离散化。

二、适用范围：数组中数量不是很多，但是数值很大

例：[-1,2,50,1000]-->[0,1,2,3]  这个映射过程就是离散化

注意：一般有负数或者是数值较大，我们会采用离散化

• 负数：因为数组中的索引时非负数，所以我们不能直接将对应的值映射到数组中的索引中，所以我们需要使用离散化。
• 如果数值非常大，加入有一个值为100000，我们总不能创建一个长度为100000长度的数组，所以我们需要进行离散化

离散化的步骤：

1. 用一个辅助数组将你需要离散化的数据保存起来（对原数组进行复制）

 //原数组 
 int[] nums={-9,5,-6,5，10000};
//辅助数组
 int[] aim= Arrays.copyOfRange(nums,0,nums.length);

      2.对辅助数组进行排序、去重

//对原数组进行去重、排序，并生成一个新的数组c 
int [] c=Arrays.stream(aim).distinct().sorted().toArray();

大体步骤： 

 二分查找的方法给大家分享代码：

    // 二分查找法
    private int find(int[] arr, int num) {
        if(arr == null || arr.length == 0){ //数组为空
            return -1;
        }
        int left=0;
        int right=arr.length-1;
        // 先找中间值
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] == num) {
                return mid;
            } else if (arr[mid] > num) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }

 二、树状数组

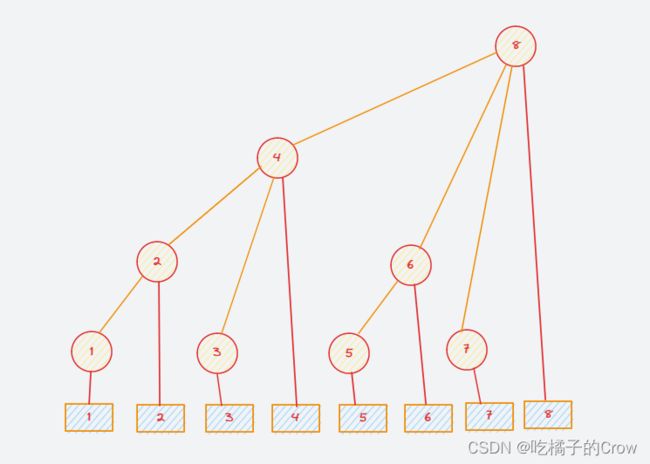
                       树状数组                                                                           二叉树

树状数组优缺点：

优点：修改和查询操作复杂度于线段树一样都是logN,但是常数比线段树小，并且实现比线段树简单。

缺点：扩展性弱，线段树能解决的问题，树状数组不一定能解决.

注意：假设我们修改了5这个结点上的值，在树状数组中我们只需要修改结点6、8上的值，那我们怎么才能决定我们修改了一个结点后修改哪些结点呢？下来我们来共同看看

 lowbit(x)运算：

 //二进制
    public int lowbit(int x){
        return x&(-x);
    }

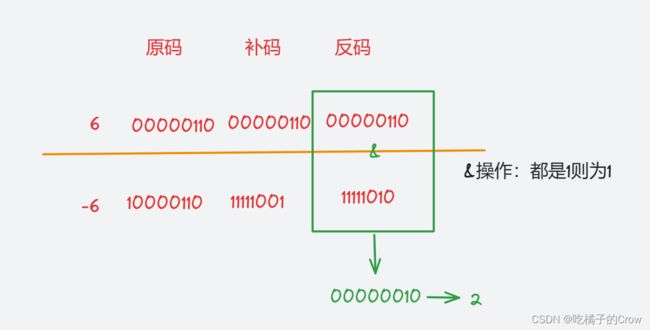
 在这里我们先复习一个数的原码、反码、补码怎么进行计算

原码：二进制    正数的最高位为0    负数的最高位为1    最高位为符号位

反码：正数的反码与原码相同     负数的反码除符号位不变，其他位置取反   0-1    1-0

补码：正数的补码与原码相同     负数的补码相当于负数的反码+1

假设我们修改的那个节点为5

5+1=6   

6+2=8 

所以不断的对i值进行lowbit操作，便可以获得下一个+值

   //树状数组进行添加元素
    public void add(int index,int val){
        for (int i = index; i 

 正推如此，倒推也是如此(比如求和，大的区间是由很多小的区间合并而来)

    //元素查询
    public int preSarch(int index){
        int sum=0;
        for (int i =index; i >0; i-=lowbit(i)) {
            sum+=this.C[i];
        }
        return sum;
    }

 如果要进行修改操作：

 public void update(int index, int val) {
        //添加的val是差值量
       this.add(index+1,val-this.A[index]);
       //更改原数组中的值
       this.A[index]=val;
    }

 树状数组源代码（模板）：

    //数组
    private int[] A;
    //树状数组
    private int[] C;
    //长度
    private int length;
     //二进制
    public int lowbit(int x){
        return x&(-x);
    }

    public NumArray(int[] nums) {
         this.A= Arrays.copyOfRange(nums,0,nums.length);
         this.C=new int[nums.length+1];
         this.length=nums.length;
         //构造树状数组，将原数组中的数添加到树状数组中
        for (int i = 0; i 0; i-=lowbit(i)) {
            sum+=this.C[i];
        }
        return sum;
    }


    public void update(int index, int val) {
        //添加的val是差值量
       this.add(index+1,val-this.A[index]);
       //更改原数组中的值
       this.A[index]=val;
    }

    public int sumRange(int left, int right) {
     return preSarch(right+1)-preSarch(left);
    }

       想必大家已经对离散化、数状数组有了大概的认识，相信这些知识能帮助你在算法的学习过程中走的更远!!!