机器学习笔记＜一＞：PCA降维详解

---

前言

本篇文章主要从对PCA的降维的直观理解、数学推导等方面对PCA降维进行讨论。

直观理解

主成分分析PCA(Principal Component Analysis)可以用于降维、数据压缩、特征提取以及数据可视化的处理。顾名思义，对数据做PCA之后可以得到数据的主成分信息，而这部分信息可以很好地还原出原数据中的信息，因此某种程度上来说，PCA是对原数据的重构或者是将原数据转换到新的坐标下进行度量(坐标系转换)。
对数据进行重构时保留了原数据中的重要信息同时消除了原数据中的冗余信息(之所以说是冗余信息是因为舍弃的那部分信息可以使用保留下来的信息表示，类似于就算矩阵秩的过程，消除线性相关的项，余下的线性无关)，冗余信息的消除在一定程度上简化了计算(特别在高维空间中尤为明显)。例如，有这样一个样本，其中有(浏览量，访客数, 下单数, 成交数, 成交金额)，一般情况下“浏览量”和“访客数”、“下单数”和“成交数”存在一定的关系(这里的“关系”是指两者的一种共变关系，即其中一个变大，另外一个也变大)，因此可以去除其中的一条记录，总体而言不会损失数据中的太多信息，而这种情况在高维空间中尤为如此。
另外数据中除了冗余信息之外，还可能有噪声，数据中的噪声不仅对后续模型的训练没有帮助，反而会降低模型的鲁棒性，因此必须对数据中的噪声加以处理。
综上所述，PCA的核心思想：使用一些新的特征代替原数据的特征，这些新特征能恰当地总结初始特征空间中包含的信息。换而言之，降维之后的数据要尽可能多地包含原数据中的信息。现在假设已经得到了降维之后的数据，欲度量降维之后的数据是否较多地包含了原数据中的信息，以此来判断新坐标系的“好坏”。如何衡量降维之后数据中包含的信息量？这里采用每个数据点于其均值之间的平均距离来度量，即方差距离(或许可以用熵来度量……)

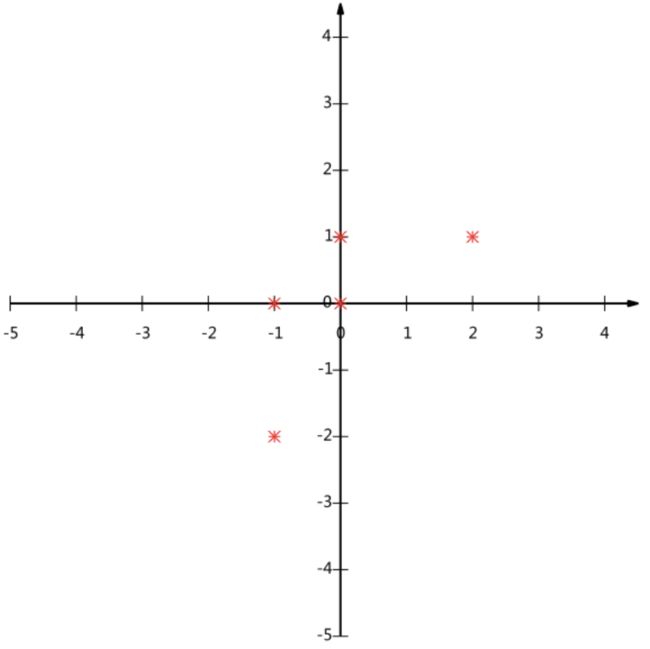
上图中的数据是二维数据，现在需要在坐标系中找得一投影方向使得该数据尽可能清楚地表示。若该投影方向是x方向，则存在两个数据点的重叠；若该投影方向是y方向，则也存在两个数据点的重叠，若投影方向是第一、三象限的角平分线，则原数据可以较好地分布在投影方向上，数据之间不存在重叠部分，如下图所示：

由上图可知，投影之后数据越分散，新的数据就可以较好地反映原数据，也就是说，投影之后的数据方差越大，其包含原数据中的信息就越多。于是PCA的问题就转换成了投影数据方差最大化的问题(解决了方差最大化问题就能找出投影方向(对于高维空间而言就是新的坐标空间)，进而计算出降维后的数据)。

数学推导

首先考虑数据之间冗余性的度量方式，这里的冗余性就是前面所说的数据的“共变”特点。先考虑两个变量的情况，一般采用协方差对其线性相关性进行度量，假这两个变量分别为$X$和$Y$,分别对应的数学期望为$u_X$和$u_Y$，则协方差的计算可表示为：$$\begin{array}{rl}Cov(X,Y)& =E[(X-u_X)(Y-u_Y)]\\ & =E[(XY-u_{Y}X-u_{X}Y+u_Y{u}_X)]\\ & =E(XY)-u_{Y}E(X)-u_{X}E(Y)+u_Y{u}_X\\ & =E(XY)-u_Y{u}_X-u_X{u}_Y+u_Y{u}_X\\ & =E(XY)-u_X{u}_Y\\ & =E(XY)-E(X)E(Y)\end{array}\text{\hspace{1em}(1)}$$式(1)说明协方差绝对值越大，则说明变量变化越大且偏离其均值很大，若协方差为正且偏大，那么这两个变量都偏向于同一方向的较大值；若协方差为负且偏小，那么这两个变量偏向于不同方向的较大值。

协方差与相关性存在一定的关系，但不完全相同，协方差为零只能说明这两个变量不存在线性相关性，不能说明二者不存在非线性相关性，只要协方差不为零就说明二者存在线性相关性；由式(2)可知，当两个变量相互独立时，协方差为零(若$X$和$Y$独立，则根据性质，$E(XY)=E(X)E(Y)$)，因为两变量独立，因此既不存在线性相关性也不存在非线性相关性，独立的条件要比协方差为零强得多。因此可由独立性得出协方差为零，但协方差为零不能得到独立性。

其实大可不必看上面那一段解释，一句话总结就是：若变量的协方差为零，则变量之间不存在线性相关性，因为这里PCA方法是以线性代数为基础，因此只考虑线性相关性(下文均采用“相关性”替代“线性相关性”)。数据中的冗余信息采用协方差矩阵来度量，协方差矩阵描述的是数据中属性之间的相关性，PCA的目标是消除数据中的冗余信息，因此只要让协方差矩阵中不同属性之间的协方差等于零，就可以消除冗余信息(使得不同属性之间不存在相关性)
假设有$N$个数据样本，每个样本有$n$个特征/属性，每个样本(n维的列向量)可表示为：$$\mathbf{x}={\left[\begin{array}{ccccc}{x}_1& x_2& x_3& \cdots & x_n\end{array}\right]}^{\mathbf{T}}$$则整个样本数据可以表示为(n行N列的矩阵)：$$\mathbf{X}=\left[\begin{array}{ccccc}{\mathbf{x}}^{(1)}& {\mathbf{x}}^{(2)}& {\mathbf{x}}^{(3)}& \cdots & {\mathbf{x}}^{(\mathbf{N})}\end{array}\right]$$矩阵的每一行表示每个样本对应的同一种属性，每一列均为一个样本，首先计算每个样本的每种属性对应的均值(即计算$\mathbf{X}$中的每一行的均值)：

$${\mu }_j=\frac{{\sum }_{i=1}^N{x}_j^{(i)}}{N};j=1,2,3,4,\dots ,n\text{\hspace{1em}(2)}$$

$\mathbf{X}$的方差表示为：

$$var(x_j)=\frac{{\sum }_{i=1}^N(x_j^{(i)}-{\mu }_j{)}^2}{N};j=1,2,3,4,\dots ,n\text{\hspace{1em}(3)}$$

式(3)在计算方差时，当样本很小时，即$N$很小时，样本方差是有偏估计，因此在样本很小时分母上常用$N-1$来校正，这样可以在很大程度上减小偏差，若样本很大，则没必要使用校正，下同。
$\mathbf{X}$的协方差表示为：

$$\begin{array}{r}cov(x_j,x_l)={\sigma }_{jl}=\frac{{\sum }_{i=1}^N(x_j^{(i)}-{\mu }_j)(x_l^{(i)}-{\mu }_l)}{N};j,l=1,2,3,4,\dots ,n\end{array}\text{\hspace{1em}(4)}$$

式(4)进行的运算为：用每个样本的每种属性减去该种属性的均值。再计算这些差值的平方和，再把所有样本的属性差值的平方和相加，最后除以N，协方差用矩阵运算可以表示为($n\ast n$的矩阵)：

$$\begin{array}{rl}\Sigma & =\frac{{\sum }_{i=1}^N({\mathbf{x}}^{(\mathbf{i})}-\mu )({\mathbf{x}}^{(\mathbf{i})}-\mu {)}^{\mathbf{T}}}{N}\\ & =\left[\begin{array}{cc}{\sigma }_1^2& {\sigma }_{12}\cdots {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_2^2\cdots {\sigma }_{2n}\\ ⋮& ⋮\\ {\sigma }_{n1}& {\sigma }_{n2}\cdots {\sigma }_n^2\end{array}\right]\end{array}\text{\hspace{1em}(5)}$$

式(5)中${\mathbf{x}}^{(\mathbf{i})}$为一个样本数据，为n维列向量，$\mu ={\left[\begin{array}{cccccc}{\mu }_1& {\mu }_2& {\mu }_3& {\mu }_4& \dots & {\mu }_n\end{array}\right]}^{\mathbf{T}}$，其对角线元素表示同种属性的方差，非对角线元素表示不同属性的协方差。
由式(4)可知，${\sigma }_{jl}={\sigma }_{lj}$，因此协方差矩阵$\Sigma$是对称矩阵，即：$\Sigma ={\Sigma }^T$
式(5)中表明每个样本列向量需要减去总体样本均值，在计算协方差矩阵的时候假设数据${\mathbf{x}}^{(\mathbf{i})}$是已经减去样本均值(已经中心化)，则此时样本对应的$\mu$=0，这样更有利于后续的计算。于是式(5)可以简写为：

$$\begin{array}{rl}{\Sigma }_{\mathbf{X}}& =\frac{{\sum }_{i=1}^N({\mathbf{x}}^{(\mathbf{i})})({\mathbf{x}}^{(\mathbf{i})}{)}^{\mathbf{T}}}{N}\\ & =\frac{1}{N}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}\end{array}\text{\hspace{1em}(6)}$$

只要使PCA降维后的数据属性之间的协方差为0，就可以达到减少原数据冗余信息的目的。假设原数据为${\hat{\mathbf{X}}}_{\mathbf{n}\ast \mathbf{N}}$，设${\hat{\mathbf{Z}}}_{\mathbf{n}\ast \mathbf{N}}={\mathbf{W}}_{\mathbf{n}\ast \mathbf{n}}{\hat{\mathbf{X}}}_{\mathbf{n}\ast \mathbf{N}}$是重构(坐标转换)后的数据(为什么原数左乘一个$n\ast n$的矩阵就可以实现数据重构?）计算重构后数据的协方差矩阵：

$$\begin{array}{rl}{\Sigma }_{\hat{\mathbf{Z}}}& =\frac{1}{N}\hat{\mathbf{Z}}{\hat{\mathbf{Z}}}^{\mathbf{T}}\\ & =\frac{1}{N}(\mathbf{W}\hat{\mathbf{X}})(\mathbf{W}\hat{\mathbf{X}}{)}^{\mathbf{T}}\\ & =\frac{1}{N}\mathbf{W}\hat{\mathbf{X}}{\hat{\mathbf{X}}}^{\mathbf{T}}{\mathbf{W}}^{\mathbf{T}}\\ & =\mathbf{W}{\mathbf{\Sigma }}_{\hat{\mathbf{X}}}{\mathbf{W}}^{\mathbf{T}}\end{array}\text{\hspace{1em}(7)}$$

欲重构后的数据无冗余信息，只要要求其协方差矩阵${\Sigma }_{\hat{\mathbf{Z}}}$非对角线元素为零即可，由式(7)可知，${\Sigma }_{\hat{\mathbf{Z}}}$对角化问题转化成了寻找一个矩阵$\mathbf{W}$对角化${\Sigma }_{\mathbf{X}}$的问题。
由线性代数的知识可知，存在一个可逆矩阵$P$可以对角化矩阵$A$，即：

$$\begin{array}{rl}{P}^{-1}AP& =\Lambda \\ & =\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]\end{array}\text{\hspace{1em}(8)}$$

上式中矩阵$P$是由矩阵$A$的特征向量构成，$P=\left[\begin{array}{cccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_3& \cdots {\mathbf{p}}_{\mathbf{n}}\end{array}\right]$，矩阵$\Lambda$由矩阵$A$的特征值组成的对角矩阵。由时(4)可知，协方差矩阵是对称矩阵，由线性代数知识可知，矩阵$A$的特征向量是两两相互正交，因此矩阵$P$是正交矩阵,因此对于正交矩阵$P$存在如下关系式：

$$P^T=P^{-1}\text{\hspace{1em}(9)}$$

将式(9)代入到式(8)中可得：$$P^{T}AP=\Lambda \text{\hspace{1em}(10)}$$对应到式(7)，假设矩阵$A$是${\Sigma }_{\hat{\mathbf{X}}}$，则变换矩阵$W=P^T$。由此便由原数据的协方差矩阵计算得出变换矩阵$W$，将变换矩阵$W$代入进式(7)就可以实现重构数据的协方差矩阵的对角化，至此消除了原数据中的冗余信息，重构后的数据表示为$\hat{\mathbf{Z}}=\mathbf{W}\hat{\mathbf{X}}$，数据$\hat{\mathbf{Z}}$还是$n$行$N$列，与原数据维度一致，只是消除了原数据中的冗余信息。
由式(10)可知，

$${\Sigma }_{\hat{\mathbf{Z}}}=P^{T}AP=\Lambda$$因此存在如下关系：$$\left[\begin{array}{cccc}{\sigma }_{1\hat{z}}^2& 0& \cdots & 0\\ 0& {\sigma }_{2\hat{z}}^2& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & {\sigma }_{n\hat{z}}^2\end{array}\right]=\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]\text{\hspace{1em}(11)}$$

由式(11)可知，特征值越大，则数据的方差越大，因此若把特征值降序排列，第一主成分就是最大特征值对应的特征向量，第二主成分就是第二大特征值对应的特征向量，依次类推。因为存在一些特征值对方差的贡献较小，因此可以将其舍弃，则只需要$k$个特征值对应得特征向量即可。假设降维后的数据维度为$k$，那数据变换矩阵取的是前$k$个主成分，于是降维后的数据可以表示为：$${\hat{\mathbf{Z}}}_{\mathbf{k}\ast \mathbf{N}}={\mathbf{W}}_{\mathbf{k}\ast \mathbf{n}}{\hat{\mathbf{X}}}_{\mathbf{n}\ast \mathbf{N}}\text{\hspace{1em}(12)}$$式(12)中的${\mathbf{W}}_{\mathbf{k}\ast \mathbf{n}}$为变换矩阵，变换矩阵的每一行由特征向量构成。至此实现减少了数据中的噪声的目标（因为在数据可视化中噪声的减少直观表现为数据维度的降低，因此该部分也可以叫做数据降维)
假设样本数据为${\mathbf{X}}_{\mathbf{n}\ast \mathbf{N}}$，样本数为$N$，每个样本有$n$个属性，下面以10个样本为例$(N=10)$，每个样本有2个特征$(n=2)$，则PCA降维步骤总结：

1.计算样本中每种属性的均值，对数据作中心化处理

$$\hat{\mathbf{X}}=\left[\begin{array}{cccccccccc}0.69& -1.31& 0.39& 0.09& 1.29& 0.49& 0.19& -0.81& -0.31& -0.71\\ 0.49& -1.21& 0.99& 0.29& 1.09& 0.79& -0.31& -0.81& -0.31& -1.01\end{array}\right]$$

上述数据是中心化之后的数据，表示为$2\ast 10$的矩阵，中心化后数据如下所示：

2.计算协方差矩阵

$$\begin{array}{rl}{\Sigma }_{\hat{\mathbf{X}}}& =\frac{1}{N-1}\hat{\mathbf{X}}{\hat{\mathbf{X}}}^{\mathbf{T}}\\ & =\left[\begin{array}{cc}0.617& 0.615\\ 0.615& 0.717\end{array}\right]\end{array}$$

3.计算特征值和特征向量

$${\lambda }_1=0.049;{\lambda }_2=1.284$$ $$p_1=\left[\begin{array}{c}-0.735\\ 0.678\end{array}\right];p_2=\left[\begin{array}{c}-0.678\\ -0.735\end{array}\right]$$

特征向量方向如上图红线所示

4.将特征值降序排序，确定主成分个数k，得到变换矩阵

主成分为：

$$p_2^T=\left[\begin{array}{cc}-0.678& -0.735\end{array}\right]$$ $$p_1^T=\left[\begin{array}{cc}-0.735& 0.678\end{array}\right]$$ 若$k=2$，则变换矩阵为：
$$\mathbf{W}=\left[\begin{array}{cc}-0.678& -0.735\\ -0.735& 0.678\end{array}\right]$$若$k=1$，则变换矩阵为：
$$\mathbf{W}=\left[\begin{array}{cc}-0.678& -0.735\end{array}\right]$$

5.计算得到降维数据

若$k=2$，则降维后的数据可由式(12)计算得到，即：

$$\hat{\mathbf{Z}}=\left[\begin{array}{cccccccccc}-0.828& 1.778& -0.992& -0.274& -1.676& -0.913& 0.099& 1.145& 0.438& 1.224\\ -0.175& 0.143& 0.384& 0.130& -0.209& 0.175& -0.350& 0.046& 0.018& -0.163\end{array}\right]$$

降维后数据分布如下所示：

若$k=1$，则降维后的数据可由式(12)计算得到，即：

$$\hat{\mathbf{Z}}=\left[\begin{array}{cccccccccc}-0.828& 1.778& -0.992& -0.274& -1.676& -0.913& 0.099& 1.145& 0.438& 1.224\end{array}\right]$$

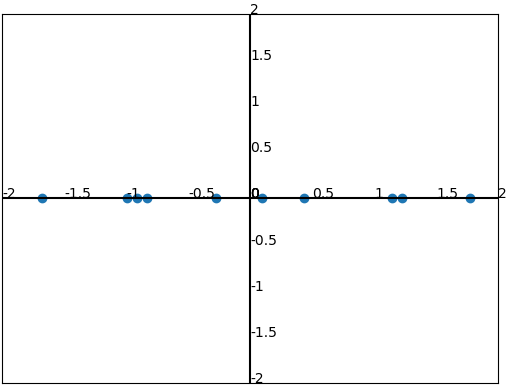
降维后数据分布如下所示：

代码实现

以鸢尾花数据集为例进行PCA处理，因为该数据集的特征的维度为4维，恰好可以通过PCA减小特征维度到3维，实现数据的可视化，可以较为直观的感受到数据的分类。

• 导入相关函数包

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets

• 定义PCA类

class PCA():
    def __init__(self):
        pass

    def central_data(self, data):
        attributes_mean = np.array([np.mean(data, axis=1)])             #计算总体样本对应的属性均值，attributes_mean.shape=(1, 4)
        mean_matrix = np.tile(attributes_mean.T, ( 1, data.shape[1]))   #构造和原始数据一样大的均值属性矩阵，mean_matrix.shape=(4, 150)
        return data - mean_matrix

    def cal_transform_matrix(self, central_data, k):
        original_cov = 1/(central_data.shape[1]-1) * central_data.dot(central_data.T)#计算协方差矩阵，original_cov.shape=(4, 4)
        eigenvalues, eigenvectors = np.linalg.eig(original_cov)         #计算特征值和特征向量
        index = np.argsort(-eigenvalues)                                #将特征值按降序排序并输出对应的索引值
        eigenvectors = eigenvectors[:, index]                           #将特征向量按降序的索引排序
        eigenvectors = eigenvectors[:, :k]                              #取前k个主成分作为转换矩阵
        return eigenvectors.T

    def reduced_data(self, transform_matrix, central_data):
        return transform_matrix.dot(central_data)                       #计算得到降维后的数据

• 定义plt_show函数

def fig_show(data, label):
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.scatter(data[0, :], data[1, :], data[2, :], c=label)
    ax.set_xlabel("first_eigenvector")
    ax.set_ylabel("second_eigenvector")
    ax.set_zlabel("third-eigenvector")
    ax.w_xaxis.set_ticklabels(())
    ax.w_yaxis.set_ticklabels(())
    ax.w_zaxis.set_ticklabels(())
    plt.show()

• 定义主函数

def main():
    pca = PCA()
    iris = datasets.load_iris()             #载入鸢尾花数据
    data = iris.data.T                      #样本数据，每一行位样本的一种属性，每一列为一个样本，data.shape = (4, 150)
    label = iris.target                     #标签数据
    central_data = pca.central_data(data)   #数据中心化
    transform_matrix = pca.cal_transform_matrix(central_data, 3)    #取前k个主成分作为变换矩阵
    reduced_data = pca.reduced_data(transform_matrix, central_data) #计算得到降维后的数据
    fig_show(reduced_data, label)           #显示降维后的数据

if __name__ == '__main__':
    main()

• 实现效果

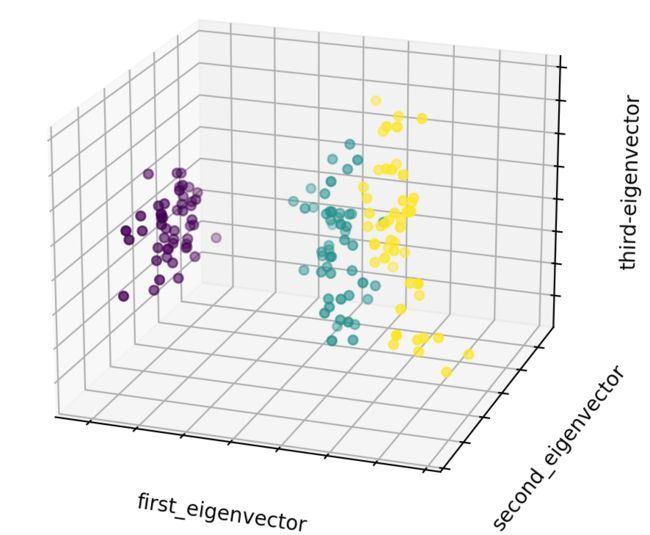
由实现效果可知，数据集经过PCA之后仍然具有较为明显的分类特征，因为在对较大数据集进行处理的时候，可以使用PCA对数据集进行预处理，减少冗余特征，能达到在一定程度上减小计算的复杂度的目的。但在一般情况下，因为丢弃了原始数据中的一些信息，就会导致模型精确度的降低，因此需要考虑精度和计算复杂度的trade-off.

PCA的局限性

• 转换过程复杂，结果难以解释；
• 计算成本昂贵，因为主要依赖于SVD，当数据量和特征点都很大时，SVD对计算能力有较高的要求；
• 对异常值非常敏感。

如何选定$k$值？

其中一种方法是采用方差所占比例来确定(由式(11)可知，这里的方差可由特征值代替)。假如采用$k$个主成分来解释方差的90%(这个可以自己设定， 如90%， 95%)的方差，则可以表示为：

$$\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3+\cdots +{\lambda }_k}{{\lambda }_1+{\lambda }_2+{\lambda }_3+\cdots +{\lambda }_n}>90\%$$

通过上式就可以通过已知的特征值来计算$k$的大小。
另外一种方法就是通过碎石检验(Scree test)来确定$k$的大小。采用绘图的方式观察与特征值随主成分个数变化的情况从而来确定$k$。如下图所示：

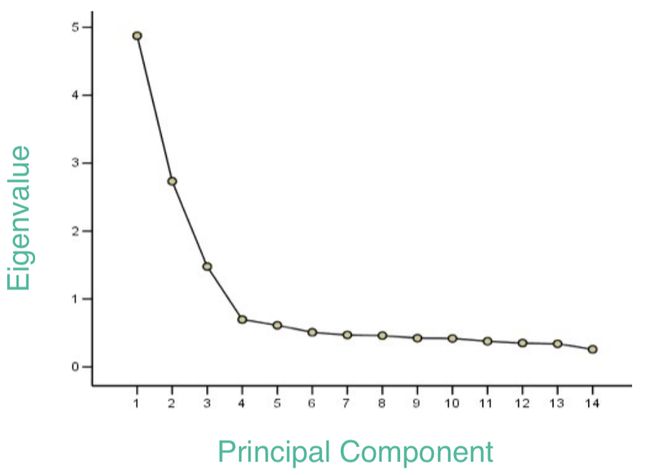
简单来说就是寻找一个因变量随自变量变化特别显著的一个点，如图，前四个主成分构成了一个“悬崖”， 而之后的10个主成分构成了悬崖下的“碎石”，到主成分4为止，特征值已经减小了很多，而且当主成分等于4时，特征值也已经很小了，后面随着主成分的增加特征值变化不大，说明再添加主成分只能增加很少的信息，所以确定主成分数$k$=4。其缺点就是大多数情况下这样变化显著的点不易确定。

为什么通过对特征值的选择可以减少噪声？

上面减少噪声的过程大概可以描述为：计算出原数据的协方差矩阵$\Sigma$，进一步计算出$\Sigma$的特征值和特征向量，对特征值进行降序排序，取前$k$个特征值对应的特征向量构成变换矩阵$W_{k\ast N}$(特征向量作为变换矩阵的行向量)，代入公式即可计算出噪声减少之后的数据$Z_{k\ast N}$。
噪声的多少一般可以采用信噪比(signal-to-noise ratio，SNR)来度量，统计学中的信噪比与信号处理中的信噪比稍有不同，下面从统计学的角度解释信噪比，其表示为方差之比，即：$$SNR=\frac{{\sigma }_{signal}^2}{{\sigma }_{noise}^2}$$若信噪比远大于1，则说明数据中含有的噪声较少，反之说明数据中含有较多噪声。一般情况，高信噪比数据的属性/特征具有较大的方差，代表了真实的数据；低信噪比数据的属性/特征具有较小的方差，而这些小方差的属性就代表了噪声，由上可知，取前k个主成分就是取前k个大的方差，删除了比较小的方差，在一定程度上消除了数据中的噪声。（更为详细的解释请参考引用的论文）

[1]机器学习及其运用
[2]精通特征工程
[3]统计学中的信噪比怎么理解呢?
[4]Phase transition in PCA with missing data:Reduced signal-to-noise ratio, not sample size!