前沿 | 数学优化视角下的深度神经网络建模与应用

目录

一、引言

二、最优化问题

1、概念

2、主要分支

3、优化算法

4、总结

三、机器学习

1、概念

2、总结

四、深度学习

1、概念

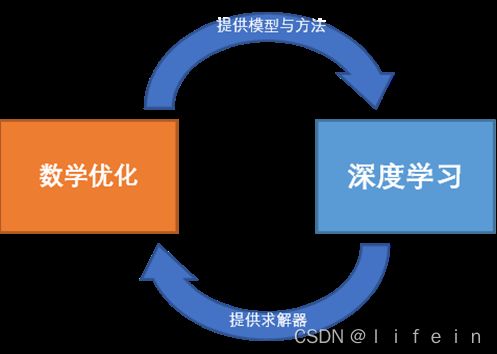
五、数学优化与深度学习之间的关系

六、应用案例

1、图像去噪——稀疏编码（from Sparse Coding）

2、图像分割——from CRF

3、白化操作——whitening

---

一、引言

        数学是一切科学的基础，是人类探索自然最为重要的语言。诺贝尔奖得主费曼曾说：“如果没有数学语言，宇宙似乎是不可以描述的。”人工智能领域也不例外。

        以 AI 技术中的机器学习及其分支深度学习为例，线性代数、概率论、统计学、微积分、信息论等数学概念都需要扎实掌握。可以说，机器学习以统计学和计算机科学为基础，以数学描述模型、指导模型为核心。

        事实上，常微分神经网络、Performer 、变分自编码器等很多优秀的模型，都是从数学角度推导出某些性质，进而构建整个模型。与此同时，模型结构与参数的性质、损失函数的收敛区间、参数空间的几何特性、最优化方法的梯度更新过程等等，都离不开数学，它是我们打开模型这一「黑盒」最为重要的工具。

 二、最优化问题

1、概念：

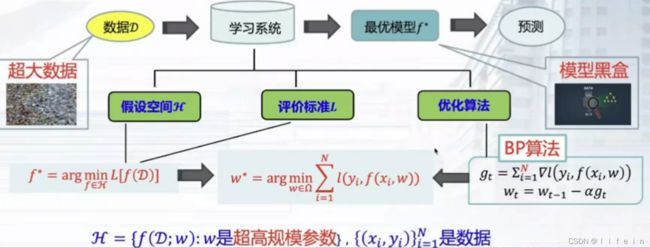
         在一个特定准则和—一个特定环境下，最大化或最小化某一特定函数或变量。通常建模为对一个函数的极小化:给定的函数f:Q→R，求x*使得

f:目标函数   Q:可行域   x*:最优解

2、主要分支：

数学规划、整数规划、动态规划、随即优化、组合优化、非凸优化……

3、优化算法∶

梯度下降法、共柯梯度法、拟牛顿法、模拟退火、遗传算法、粒子群算法……

4、总结：

最优化问题就是在优化曲面上寻找极值点的过程。 

三、机器学习

1、概念

        假设y=F(x)是问题世界的模型，z=N(x)是观测环境噪音，样本集是在噪音环境下，经过有限次观察，从问题世界获得的一组观测数据，记为 S(z, {,})。它是问题世界所有可能观测数据的一个子集。从样本集S(z,  {,})学习(估计)一个假设f(x)，使得f(x)是问题世界模型F(x)的一个近似。

机器学习基本模型

F:假设空间  D:数据集  l:损失函数  argmin:优化算法

2、总结：

1）机器学习的基本模型——基于一定的观测数据，得到模型，这个模型能在观测的数据上有一个最小的函数。

2）机器学习中有模型、数据和决策函数。基于这个决策函数优化的过程往往用到不同的最优化的方法。

 四、深度学习

1、概念：

        深度学习是由多个非线性变换复合而成的网络模型。主要用于对数据生成机制的模拟(表示、特征提取)、对未知映照关系的逼近。深度学习主要关注网络设计网络学习和泛化性三个问题。

        深度学习的数据标注非常多，深度学习通多黑盒模型或者非常严格设计的网络结构，来构建损失函数。

五、数学优化与深度学习之间的关系

 六、应用案例

1、图像去噪——稀疏编码（from Sparse Coding）

稀疏性假设∶
自然图像( Natural image)可以很好地表示为几个基的线性组合。

噪声图像（Noisy images)通常不遵循稀疏假设。

        构建一组基函数，在基函数下面做线性表达，希望约束这个线性表达是比较稀疏的（通过一范数来进行刻画）。针对original的信号来刻画有一个表达能尽可能的接近最小值，且要求系数是绝对稀疏的。

图像去噪分为三大类：基于滤波器的方法（Filtering-Based Methods）、基于模型的方法（Model-Based Methods）和基于学习的方法（Learning-Based Methods）

2、图像分割——from CRF

1）条件随机场构建能量模型，形成能量函数。

2）深度学习兴起以后，可以通过全卷积神经网络/Transformer结构来实现。

但是全卷积神经网络效果不好→在最后添加CRF来优化

 模型实现：

只在组后增加一个CRF则没有很好，则转化为CRF-RNN来实现。

CRF-RNN：

        基于CRF模型优化的方式进行了unfolded solution得到一个网络结构，创作网络神经结构。串在原来的后面来进行端到端的训练。

ps.条件随机场（CRF或CRFs）与隐马尔科夫模型有着千丝万缕的联系。

马尔科夫链是指具有马尔可夫性质且存在于离散指数集合状态空间内的随机过程。那么什么是马尔科夫性质呢？

从定义上来说，当一个随机过程在给定现在状态及过去所有状态的情况下，其未来状态的条件概率分布仅依赖于当前状态；换句话说，在给定现在状态时，其过去状态（即该过程的历史路径）是条件独立的。

3、白化操作——whitening

1）概念：

        将各向异性的特征(每一列是一个特征，每一行是一条数据)，转化为各向同性，大家(不同特征)在一个尺度下。既然原始的特征，各自的分布在空间中拥有不同的“旋转”和“拉伸”，那么我们找到每一个特征相对于“标准正交基”的“旋转”和“拉伸”，进行反向操作，大家就都又恢复到了“同一个尺度”下。

        白化处理是一种图像处理技术，可以通过调整图像的颜色、对比度等参数，使图像看起来更加美观或符合特定需求。

2）作用：

跳出局部极值，提升优化的收敛速度。

文章内容部分参考： 

张兆翔，中国科学院自动化研究所研究员、博导，教育部长江学者，国家万人计划青年拔尖人才。

---

有任何问题，欢迎在下方评论留言。

更多机器学习内容，详见个人主页：(12条消息) ｌｉｆｅｉｎ的博客_CSDN博客-Python,Python可视化,SQL SERVER领域博主https://blog.csdn.net/m0_60066036?spm=1018.2226.3001.5343