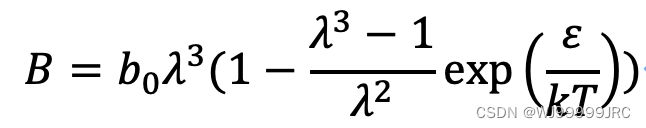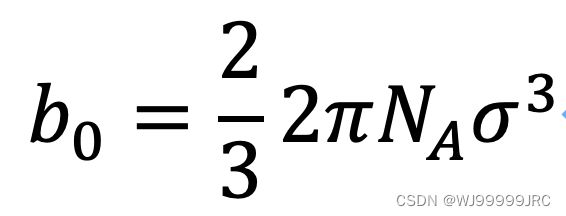用Python分析方阱位能函数与Lennard-Jones 位能函数的近似关系
在我们研究微观世界分子间的相互作用时,分子间的相互作用力是无法避开的话题。然而,分子间作用力十分复杂,大部分作用力原理的研究尚停留在定性描述阶段。不过,我们可以将分子间作用力分为斥力和引力两大类,以方便我们的研究。故人们为了研究分子间的斥力和引力,便构造了经验的位能函数,以便更好地分析分子间的作用力。位能函数模型十分重要,目前已构成了现代统计力学计算和计算机分子模拟的基础。
下面我们讨论两种最为常见的位能函数,即方阱位能函数与Lennard-Jones 位能函数。并分析它们之间的关联,这有助于我们更加深入而形象地理解分子间作用力的效果。
1.方阱位能函数
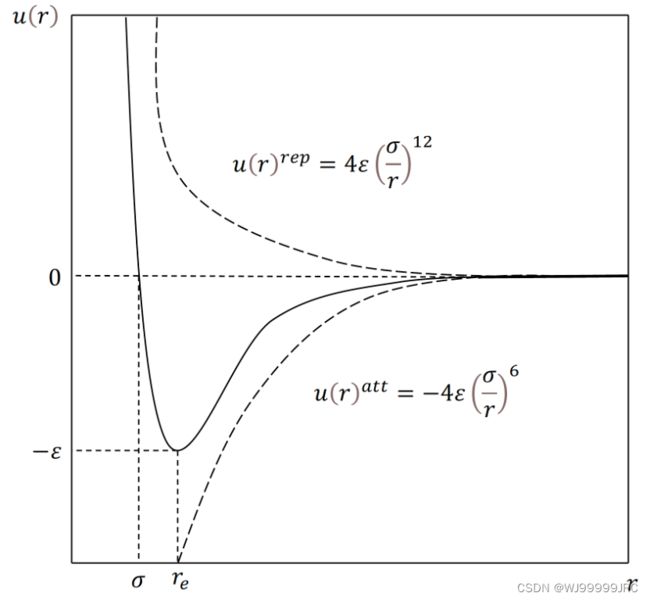
方阱(square-well) 位能函数是一个最简单的同时考虑分子间排斥和吸引两种相互作用的位能函数。该模型假设分子间吸引力仅在分子间距 r 的一定范围内存在,且为常数。其位能函数如下:
方阱位能模型将分子看成直径为σ的硬球,而吸引力仅在σ<r≤λσ的范围内存在,且为不随r变化的常数-ε,好像分子周围存在一个方阱,阱宽为σ(λ-1),阱深为ε。
图1 方阱位能函数
方阱(square-well) 位能函数数学处理简单又具有3个可调参数σ、ε和λ,因此在理论计算和分子模拟中仍得到广泛应用。
2.Lennard-Jones 位能函数
最早由数学家琼斯于1924年提出。由于其解析形式简单而被广泛使用,特别是用来描述惰性气体分子间相互作用尤为精确。其位能函数如下:
该模型也将分子看作直径为该模型也将分子看作直径为σ的硬球,与方阱位能函数不同,该模型假设分子间作用力由分子间引力与斥力共同作用导致。引力项与斥力项如下:
虽然既考虑了斥力作用又考虑了引力作用,但分子间距离等于硬球直径σ时,排斥力陡升至无穷大,而大于σ时又完全忽略了分子间斥力作用,只考虑分子间引力的作用,因而对分子间作用力的描述仍是粗糙的。
图2 Lennard-Jones 位能函数
3. 使用方阱位能函数模拟的可行性与必要性
通过上述的分析,我们可以发现方阱位能函数与Lennard-Jones 位能函数具有相同的两个可调参数,即硬球分子直径σ与势能最低值ε。因此,使用方阱位能函数来近似模拟Lennard-Jones 位能函数是可能的。
与Lennard-Jones 位能函数相比,方阱位能函数的积分计算要简单许多。例如,当我们需要通过位能函数计算第二维里系数时,需计算积分:
上式中NA为阿伏伽德罗常数,k为玻尔兹曼常数。
如果我们使用方阱位能函数则积分式可以化简如下:
可见,方阱位能函数计算非常简便。而只需调节方阱模型中的λ参数,我们就可以获得对Lennard-Jones 位能函数的合理模拟。
4. 用方阱位能函数模拟Lennard-Jones 位能函数
首先,我们对两个位能函数模型进行“归一化”处理,使得λ为唯一参数。即考虑u(r)ε与r/σ之间的关系。那么,方阱位能函数可改写为:
而Lennard-Jones 位能函数可以改写为:
对于以上两个函数,我们只需考虑一个参数也就是方阱位能函数模型中的λ。改变λ的值即可以实现对Lennard-Jones 位能函数的近似。下面,我们通过python来实现这一过程。
首先导入必要的libraries:
import numpy as np
import matplotlib.pyplot as plt
下面我们分别在python中定义两个位能函数,注意方阱位能函数中的R(λ)值需要调整。具体过程如下:
# L_J potential energy
def L_J(r):
u = 4 * ((1/ r) ** 12 - (1 / r) ** 6)
return u
# S_W potential energy
@np.vectorize
def S_W(x):
if x <= 1:
return 0
elif 1 < x < R:
return -1
elif x > R:
return 0
# estimate R_value
R = 1.11
print("R =",R)下面我们分别产生两个位能函数的自变量,注意在我们归一化以后,只需要讨论【1,4】区间上的函数图像即可,因为随着分子间距r的进一步增大,两种模型的位能都趋近于0。
# Create a range of distances for L_J
r = np.linspace(1, 4.0, 100)
u = L_J(r)
# Create a range of distances for S_W
x = np.linspace(1, 4, 1000)
y = S_W(x)最后我们再将两个位能函数的图像画出,代码如下:
# Plot the potential energy curve
plt.xlabel('r_Distance (r/σ)')
plt.ylabel('r_Potential Energy (E/ε)')
plt.plot(r, u, label='L_J')
plt.plot(x, y, label='S_W')
plt.grid(True)
plt.legend()
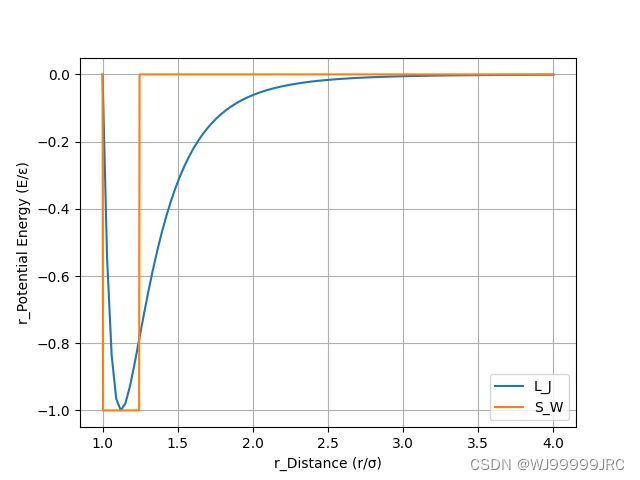
plt.show()通过调整R值,我们可以看到:通过改变R值,橘黄色曲线的右半部分会移动,且R越大越向左偏移,偏移的位置的横坐标即为R的值。
图3 R = 1.25时的运行结果
图4 R = 3.11时的运行结果
运行代码并不断调整R值之后, 我们得到:R取1.11左右时,可以得到对Lennard-Jones位能函数的最好模拟。
图5 R = 1.12时的运行结果
因此,当方阱位能函数中的R(λ)值取1.12时,我们可以获得其对Lennard-Jones位能函数的最好模拟结果。
5. 结果分析
方阱位能函数与Lennard-Jones位能函数随着分子间距离的增加,位能基本都存在一个从正无穷降到最低位能-ε再增加直到趋近于0的一个过程。关健就在于Lennard-Jones位能函数极值点的取得。
对于归一化的Lennard-Jones 位能函数:
我们通过python来做出其导函数的图像,导数的零点即为原函数的极值点:
# L_J potential energy derivative
def d_L_J(r):
v = 4*(-12*(1/r)**13+6*(1/r)**7)
return v并通过如下代码标出其第一个极值点,即r = 1.12
plt.plot(r, u, label='L_J')
plt.plot(r, v, label='d_L_J')
plt.axhline(y=-0.1439, linestyle='--', color='red')
plt.axvline(x=1.12, linestyle='--', color='red')
plt.grid(True)
plt.legend()
plt.show()运行代码后,我们得到:
因此,当归一化后的Lennard-Jones 位能函数取最小值-1时,r/σ应取1.12,也就是方阱位能函数为了模拟Lennard-Jones 位能函数的的R(λ)的取值。