数据结构学习记录——树习题-Complete Binary Search Tree(题目描述、输入输出示例、数据结构的选择、核心算法、计算左子树的规模)
目录
题目描述
输入示例
输出示例
数据结构的选择
核心算法
计算左子树的规模
思路
总结
题目描述
现给定一系列不同的非负整数键，如果要求构造出一颗完全二叉树，则可以构造唯一的二叉搜索树。输出此二叉搜索树的层序遍历序列。
完全二叉树
有n个节点的二叉树，对树中节点按从上至下、从左到右顺序进行编号，编号为i（1<= i <= n）节点与满二叉树中编号为i节点在二叉树中位置相同。
二叉搜索树
一颗二叉树，可以为空；如果不为空，满足一下性质：
1.非空左子树的所有键值小于其根节点的键值。
2.非空右子树的所有键值大于其根节点的键值。
3.左、右子树都是二叉搜索树。
输入示例
每个输入文件包含一个测试用例。
对于每种情况，第一行包含正整数N（≤ 1 0 0 0）。
然后下一行给出了 N个不同的非负整数键。一行中的所有数字都用空格分隔，不大于2000。
Sample Input:
10
1 2 3 4 5 6 7 8 9 0
输出示例
对于每个测试用例，在一行中打印相应的完全二叉搜索树的层序遍历序列。
一行中的所有数字必须用空格分隔，并且行的末尾不能有额外的空格。
Sample Output:
6 3 8 1 5 7 9 0 2 4
数据结构的选择
二叉树可以通过数组和链表来实现，我们现在要先确定一下用哪种数据结构来解决这道题目。
在之前的学习中，我们使用链表来实现二叉树的存储。因为在一些较为极端的情况下，二叉树可能向左或向右倾斜的程度比较大，这个时候使用数组来实现的话就会造成很大的空间浪费。这是从空间的一个角度来考虑的，而在遍历上，数组和链表两种实现方式都是差不多的。
现在看回这道题目，它需要进行的操作：
- 填写数字（也属于某种遍历）
- 层序遍历
在遍历的角度上来看，两种方式都差不多，所以不考虑了。
从空间的角度上来看，完全二叉树的情况下，数组是不会浪费空间的，故而还不能下定论。
最后看到遍历的方式，发现是层序遍历，这就意味着，如果使用数组实现，那么直接顺序输出就是其层序遍历的遍历序列；而链表的层序遍历需要借助队列来实现，显然更为复杂一点。
所以，我们选择数组来实现。
核心算法
void solve(int ALeft, int ARight, int TRoot)
{
/* 初始调用为 solve(0, N - 1, 0) */
n = ARight - ALeft + 1;
if (n == 0)
return;
L = GetLeftLength(n); /* 计算出n个结点的树其左子树有多少个结点 */
T[TRoot] = A[ALeft + L];
LeftTRoot = TRoot * 2 + 1;
RightTRoot = LeftTRoot + 1;
solve(ALeft, ALeft + L - 1, LeftTRoot);
solve(ALeft + L + 1, ARight, RightTRoot);
}其中A为排序后的序列，我们需要对输入的序列进行排序，才能得到它， ALeft表示序列最左边的位置的下标，ARight则表示序列最右边的位置的下标。
T是我们求的结果树，TRoot就是结果树的根结点。
除了排序之外，还有一步重要的操作：计算左子树的结点个数，只有确定了左子树的结点个数，我们才能确定根结点以及右子树。
计算左子树的规模
思路
如图所示，完全二叉树的完美二叉树的部分可以用
来表示其结点数，H为其中完美二叉树部分的层数。
接下来把剩余的几个结点个数设为X，总结点数设为N，就可以得到一个关系式：
将公式整理成log形式，得：
对于大规模的计算，X对整体的结果影响很小很小，我们把X忽略，故而有：
N是已知的，所以可以根据这个公式求出H；
继而代入求出X；
现在得到一整棵完全二叉树的结点数了，要怎么求其左子树的结点呢？
一棵完全二叉树的左子树也一定是一棵完全二叉树，所以可以知道其左子树的结点数应为：
你以为，这样就完了吗？
看一下另外一种情况，我们就会发现目前的X还不是最正确的X：
很显然，这里的X已经不在左子树的范畴内了。
正确应该为：
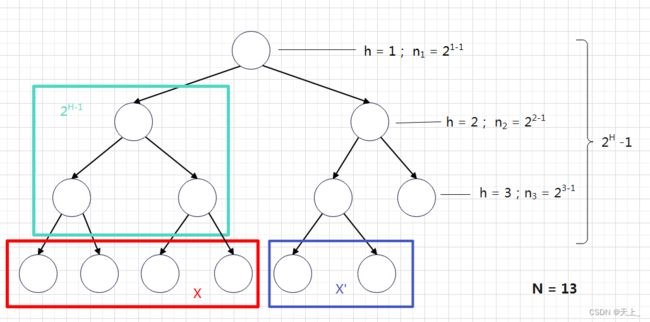所以我们应该要对X的取值有一定的限制，或者说，X应该要有一定的范围。
可以考虑，当左子树为一棵完美二叉树时，X可以为0，也可以为
。
X为0的情况：
X为 的情况：
总结
最后，总结一下计算左子树的规模：
第一步是通过公式求出H；
第二步是通过公式求出X；
第三步是选出正确的X，
最后一步就是代入 求出我们最终的结果。
end
学习自：MOOC数据结构——陈越、何钦铭