编程范式-结构化编程

本系列文章会依次介绍三个主要的编程范式，它们分别是结构化编程（structured programming）、面向对象编程（object-oriented programming）以及函数式编程（functional programming），本文聚焦在结构化编程。

非结构化编程

非结构化程序设计是历史上最早的能够创造图灵完备算法的程序设计模式。非结构化程序设计语言既有高阶语言，也有低阶语言。一些语言通常被印证为非结构化语言，包括JOSS、FOCAL、TELCOMP、汇编语言、MS-DOS批处理和早期版本的BASIC、Fortran、COBOL和MUMPS。

非结构化程序设计被批评最严重的方面就是会产生很难读懂的代码（戏称面条式代码），在创建大型工程方面有时会被认为是很差的，不过，因为赋予程序设计者很大的自由，被人称赞为如同莫扎特在谱曲。

特点1 : 行号和GOTO

一个使用非结构化语言的程序经常包含按顺序排列的命令或声明，通常每个都占用一行。每一行都有编号或者标签，这样程序中的任意行都可以被执行。

在BASIC等未结构化的程式语言中，行号也用来标示分支指令的目的地。例如：

10 IF X = 42 GOTO 40 '最前面的"10"是行号,X=42时会跳到行号=40的程式码,否则会跳到下一行
20 X = X + 1
30 GOTO 10'跳到行号=10的程式码
40 PRINT "X是42!"'输出"X是42!"

一般认为Goto型式的分支是比较差的程式风格，因为容易形成复杂而难以理解的面条式代码

像是C语言及C++之类的语言仍保留GOTO指令，不过GOTO的目的地已改用标记标示。这类的GOTO指令一般也不建议使用，只建议在少数情形下使用，例如跳出多重回圈：

while(1) {
  while (1) {
    if (done) {
      goto freedom;
    }
  }
}
freedom:

上述的程式可以和以下不使用GOTO的程式比较，以下的程式需在不同位置依done变数值进行判断，相较之下，上述的程式可读性较高。也证明了goto语句能被改写非goto语句。

while(1) {
  while (1) {
    if (done) {
      break;
    }
  }
  if (done) {
    break;
  }
}

除了C/C++之外，有些人会指出，Java中的带命名的break语句或者Exception都和goto很类似。事实上，这些语法结构与老的编程语言（类似FORTRAN和COBOL）中的完全无限制的goto语句根本不一样。就算那些还支持goto关键词的编程语言也通常限制了goto的目标不能超出当前函数范围。

特点2: 面条式代码

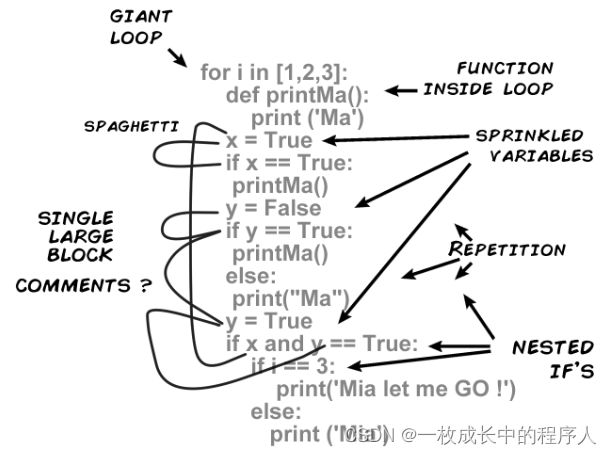
面条式代码（Spaghetti code）是软件工程中反面模式的一种，是指源代码的控制流程复杂、混乱而难以理解，尤其是用了很多GOTO、例外、线程、或其他无组织的分支。其命名的原因是因为程式的流向就像一盘面一样扭曲纠结。

一方面，当使用各种汇编语言（及其底层的机器语言）或者脚本时，非常容易编写出面条式代码。其原因是由于这些低级语言很少有可以对应 FOR 循环或 WHILE 循环的机制。

另外一方面，哪怕在现在比较流行的高级语言中，由于没有经验或者工匠精神的程序设计师，或长期频繁修改的复杂程序，也很容易形成面条式的代码。

for i in [1,2,3]:
    def printMa():
        print ('Ma')
    x = True
    if x == True:
     printMa()
    y = False
    if y == True:
     printMa()
    else:
     print("Ma")
    y = True
    if x and y == True:
        if i == 3:
            print('Mia let me GO !')
        else:
           print ('Mia')

高阶语言的面条式代码

结构化编程

结构化程式设计（Structured programming），一种编程典范。它采用子程序、块结构、for回圈以及while回圈等结构，来取代传统的 goto。希望借此来改善计算机程序的明晰性、品质以及开发时间，并且避免写出面条式代码。

一些有趣的历史

Dijkstra很早就得出的结论是：编程是一项难度很大的活动。一段程序无论复杂与否，都包含了很多的细节信息。如果没有工具的帮助，这些细节的信息是远远超过一个程序员的认知能力范围的。而在一段程序中，哪怕仅仅是一个小细节的错误，也会造成整个程序出错。

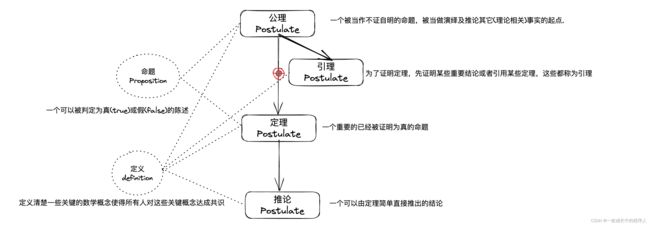
Dijkstra提出的解决方案是采用数学推导方法。他的想法是借鉴数学中的公理（Postulate）、定理（Theorem）、推论（Corollary）和引理（Lemma），形成一种欧几里得结构。Dijkstra认为程序员可以像数学家一样对自己的程序进行推理证明。

公理化系统

公理化系统最初由欧几里得建立，目的是以一套标准化的流程来建立一个严谨的理论体系。简单而言，公理化系统就是选出一组不证自明的最为基础的公理集，然后以这些公理作为基石证明推导出其他关键定理。由此可以形成一个完备的数学理论体系，例如欧几里得建立的欧氏几何理论。公理化系统有三个重要性质，分别是自洽性(consistent), 独立性(independent), 完备性(complete)。具有这样的性质的公理系统就是好的公理系统。

换句话说，程序员可以用代码将一些已证明可用的结构串联起来，只要自行证明这些额外代码是正确的，就可以推导出整个程序的正确性。当然，在这之前，必须先展示如何推导证明简单算法的正确性，这本身就是一件极具挑战性的工作。

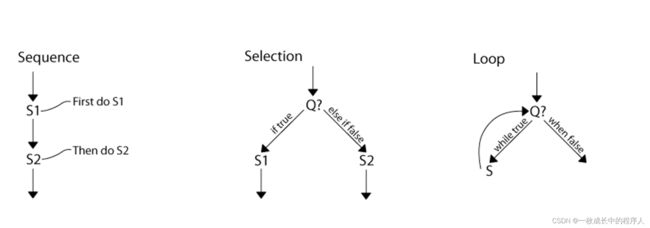
在1960年代开始发展，科拉多·伯姆及朱塞佩·贾可皮尼（Giuseppe Jacopini）于1966年5月在《Communications of the ACM》期刊发表论文，证明了，人们可以用顺序结构，条件结构和循环结构来构造出任意的程序，也说明任何一个有goto指令的程式，可以改为完全不使用goto指令的程式

 顺序、分支和循环结构

这个发现非常重要，因为他证明了我们构建可推导模块所需要的控制结构集与构建所有程序所需的控制结构集的最小集是等同的，这样依赖结构化编程就诞生了。

Dijkstra在研究过程中发现了一个问题：goto语句的某些用法会导致某个模块无法被递归拆分成更小的、可证明的单元，这会导致无法采用分解法来将大型问题进一步拆分成更小的、可证明的部分。

Dijkstra在1968年提出著名的论文《GOTO陈述有害论》（Go To Statement Considered Harmful），因此结构化程式设计开始盛行。但是，goto也不乏强烈支持者。总之，这场火热的争论持续了超过10年。现如今，无论是否自愿，我们都是结构化编程的践行者了，因为我们的编程语言基本都禁止了不受限制的直接控制转移语句。

本质思想

结构化编程的本质思想是：对程序控制权的直接转移进行了限制和规范，使用goto这样的无限制跳转语句将会损害程序的整体结构。主张和证明了一切程序设计都可以用顺序结构、分支结构、循环结构进行编程。

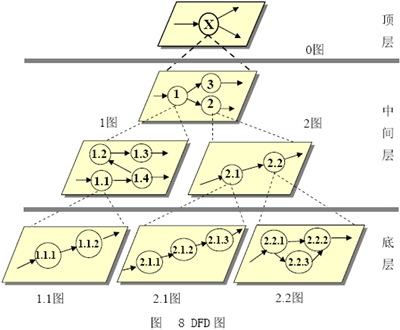
结构化程序设计

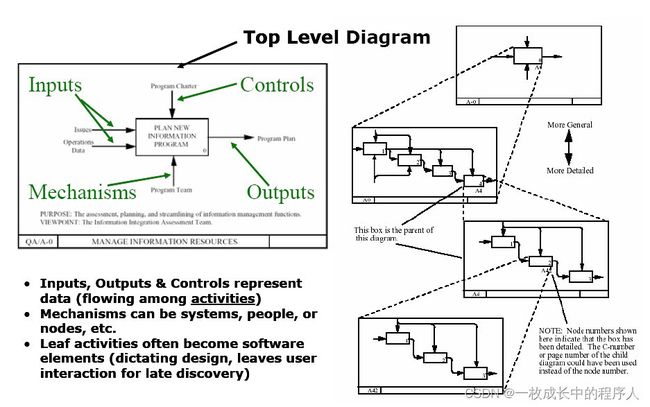
Dijkstra在1968年提出著名的论文《GOTO陈述有害论》（Go To Statement Considered Harmful），因此结构化程式设计开始盛行。核心思想是将一个复杂的软件工程项目，递归拆解为一个个可推导和可证明的函数，每个被拆分出来的函数可以用结构化编程范式来书写。

本文不展开程序设计模式，后续单独进行结构化程序分析和设计篇章进行讲解。