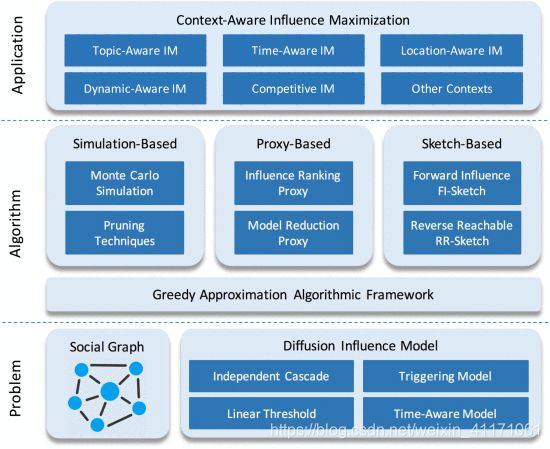
在线社交网络的影响力最大化算法

1. 病毒式营销

针对社交网络中最有影响力的用户（例如，通过向他们提供免费或价格优惠的样本），人们可以通过口碑利用网络效应的力量，从而将营销信息传递到网络的很大一部分。

2. 影响力最大化：病毒式营销的关键算法

在一个在线社交网络中选择一组k个用户，即选出具有最大影响力传播的种子集，然后通过信息传播中的种子集来影响用户的预期数量最大。

2.1. 定义：扩散模型和影响扩散

给定社交图 $G=(V,E)$，一个用户集 $S\subseteq V$，扩散模型$M$捕获$S$在$G$上传播信息的随机过程。$S$的影响力扩散（也称为影响力函数），以${\sigma }_{G,M}(S)$表示，是受$S$影响的预期用户数（例如，在病毒性营销中采用新产品的用户），其中${\sigma }_{G,M}(\cdot )$是在用户的任何子集上定义的非负集合函数，即${\sigma }_{G,M}:2^V\to R\ge 0$。

2.2. 定义：影响最大化(IM)

给定社交图$G$，扩散模型$S$和一个正整数$k$，IM从$V$选择一套$k$用户的$S^{\ast }$作为种子集以最大化影响力传播${\sigma }_{G,M}(S^{\ast })$。
直观地讲，影响力函数$\sigma (\cdot )$在很大程度上取决于扩散过程。
给定:
- 定向社交网络
- 与边缘相关联的一组权重，代表用户之间影响的强度或概率
- 一个随机影响传播模型，用于控制某种行为将如何在用户中扩散
- 基数约束k，用于识别k个节点的集合，称为“种子集”，可以有针对性地最大化受影响的节点的预期数量

2.3. 扩散模型

通用扩散框架：框架关联每个用户$\ddot{u}\in V$状态为无效或活跃。然后，基于社交图$G$，它考虑了用户之间的以下传播过程。最初，一组选定用户（称为种子集 $S\subseteq V$）处于活动状态，而其他用户在$V$中不活跃。然后，考虑种子用户$S$所处的扩散过程可以“影响”其邻居以使其活跃，新激活的用户可以进一步激活其邻居，依此类推。当没有新用户可以激活时，此传播过程终止。特别是，该框架将上述“激活”建模为一个随机过程，影响力在不断扩大。然后定义影响力传播$\sigma (S)$为在扩散过程终止后具有活动状态的预期用户数。

在此调查中，我们关注渐进式扩散模型，即，由于大多数IM算法都考虑了渐进式模型，因此不能在以后的步骤中停用已激活的节点。也存在非渐进式扩散模型，即可以在非渐进模型中停用激活的节点。典型的非渐进式扩散模型是SIR/SIS模型和Voter模型。

2.3.1. 代表性模型

• 独立级联（IC）模型
• 线性阈值（LT）模型
• 触发（TR）模型
• 时间感知模型

区别：采用不同的机制来捕获用户如何切换其状态从非活动状态到活跃的，这是由它的邻居的影响。

2.4. 挑战

- 如何对社交网络中的信息传播过程进行建模，这将严重影响IM中任何种子集的影响传播。
- 获得IM的最佳解是NP-hard。
- 由于信息传播的随机性，即使对任何单个种子集的影响传播进行评估也是计算复杂的。
- 要检索（接近）最佳种子集并同时缩放到庞大的社交图非常具有挑战性。
- 解决上下文感知的影响最大化问题会带来许多技术挑战：将IM与各种环境（例如位置，时间和主题）结合提供了机会信息，以提高IM的有效性。

2.5. 框架

3. 影响力最大化的主要算法

尽管IM问题通常在计算上很复杂，但是当影响力函数$\sigma (\cdot )$满足单调性和亚模态时，可以估计出最佳解。(monotonicity and submodularity)
IC，LT，TR和CT模型下的影响函数是单调和亚模的。 尽管IM的最佳解决方案很难解决，仍旧可以利用单调性和亚模性以理论上的合理性为IM提供有效的近似解决方案。

3.1. 贪婪框架

现有的大多数IM算法都采用简单的贪婪框架。使用空种子集初始化该$S$，并反复选择一个节点$\ddot{u}$进入$S$，如果$\ddot{u}$为影响函数提供最大的边际收益 。当存在$k$个不同节点在$S$时，算法终止。

3.2. 现有IM算法的分类和比较

尽管前面提到的贪婪框架具有很好的近似比率，即时通讯仍然很难解决，因为评估$\sigma (\cdot )$仍旧是#P-hard问题。

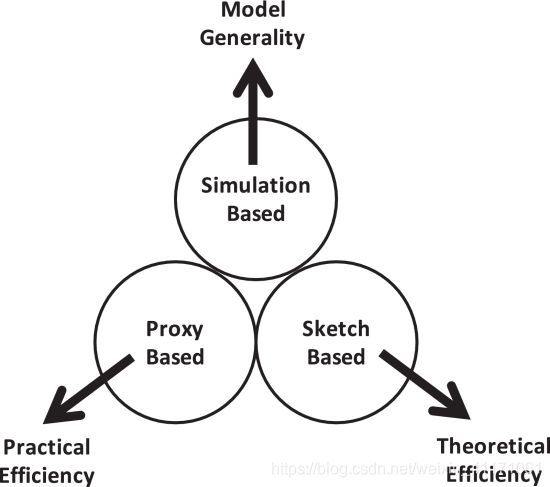
3.2.1. 基于仿真的方法：模型通用性

关键思想：执行蒙特卡洛（MC）仿真以评估影响力分布$\sigma (S)$任何种子集$S$。
优点：具有模型通用性的优点。换句话说，通过插入特定于模型的MC仿真模块来评估影响，它可以轻松地合并任何扩散模型。此外，该方法具有良好的理论特性，如果基础影响函数是单调和亚模的，则通常返回具有恒定有界比的解。
缺点：计算效率 。此方法必须生成许多样本实例才能获得对$\sigma (\cdot )$误差很小，这会导致大量的计算开销。

3.2.2. 基于代理的方法：实际效率

关键思想：设计代理模型来近似影响函数$\sigma (S)$克服#P-hard。从理论上讲，评估$\sigma (S)$是复杂的，因为$S$可能会通过图中的大量路径潜在地影响其他用户。但是，这种方法认为，可以将复杂的影响力模型有效地简化为代理模型，例如PageRank或最短路径。
优点：实用高效。例如，仅考虑最短路径，对$\sigma (S)$是多项式的而不是#P-hard。这种方法中的许多算法都显示了基于代理的方法的经验效率优势。
缺点：尽管基于代理的方法通常可以提高实践效率，但是它缺乏理论上的保证。已经表明，在某些情况下，基于代理的方法是不稳定的（最佳种子集和相应的影响可能会随着基础图的微小变化而急剧变化）。由于基于代理的解决方案通常对不稳定的情况不敏感，因此它们可能是任意坏的。

3.3.3. 基于草图的方法：理论效率

关键思想：设计一种在理论上有效的解决方案（而不是仅实际有效的方案），该解决方案还保持恒定的近似比率，从而克服了上述两种方法的缺点。例如，获得解决方案的预期时间复杂度与具有恒定逼近率的输入图的大小几乎呈线性关系。这种方法的想法是首先在扩散模型下构建理论基础的草图。然后，该方法基于构造的草图加快了评估速度，以评估影响函数。
优点：理论结果，即，它是具有严格约束解决方案和经验证的低​​时间复杂度的最理论上有效的算法。
缺点：构造的草图必须与基础扩散模型对齐。因此，与基于仿真的方法相比，该方法的理论结果不适用于更大范围的扩散模型。另外，基于草图的方法的实际效率可能比基于代理的方法的实际效率差，因为它需要确保最坏情况下的近似率。

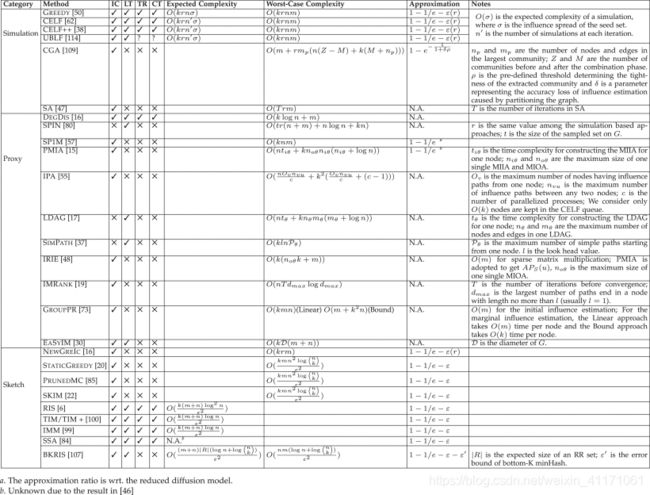
3.3.4. 比较表格

上表. 经典扩散模型下影响最大化算法的比较

• 从第3列到第6列，指出比较的算法是否支持不同的扩散模型（“✓”表示支持，“✗”表示不支持，“？”表示可能支持，但没有明确说明）。
• 在第7列和第8列中，分别给出了算法的预期和/或最坏情况下的复杂度。
• 在第9列中，声明了IM的算法的近似比率（不保证近似比率的“ NA”；对于基于代理的算法，给定的近似比率适用于其代理模型）。

4. 相关代码

1. Ç. Aslay, N. Barbieri, F. Bonchi and R. A. Baeza-Yates, “Online topic-aware influence maximization queries”, Proc. Extending Database Technol., pp. 295-306, 2014.
   代码：C语言
2. D. Kempe, J. Kleinberg and E. Tardos, “Maximizing the spread of influence through a social network”, Proc. 9th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, pp. 137-146, 2003.
   代码：Julia
3. Y. Tang, Y. Shi and X. Xiao, “Influence maximization in near-linear time: A martingale approach”, Proc. ACM SIGMOD Int. Conf. Manage. Data, pp. 1539-1554, 2015.
   代码：Scala
4. A. Goyal, F. Bonchi and L. V. S. Lakshmanan, “Learning influence probabilities in social networks”, Proc. 3rd ACM Int. Conf. Web Search Data Mining, pp. 241-250, 2010.
   代码：Python
5. Content-based Network Influence Probabilities: Extraction and Application
   代码：Python
6. A. Goyal, W. Lu and L. V. S. Lakshmanan, “Simpath: An efficient algorithm for influence maximization under the linear threshold model”, Proc. IEEE 11th Int. Conf. Data Mining, pp. 211-220, 2011.
   代码：C++
7. X. He and D. Kempe, “Stability of influence maximization”, pp. 1256-1265.
   代码：C++, Python, MATLAB
8. N. Ohsaka, T. Akiba, Y. Yoshida and K.-I. Kawarabayashi, “Fast and accurate influence maximization on large networks with pruned monte-carlo simulations”, Proc. 28th AAAI Conf. Artif. Intell., pp. 138-144, 2014.
   代码：C++
9. S. Lei, S. Maniu, L. Mo, R. Cheng and P. Senellart, “Online influence maximization”, Proc. 21th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, pp. 645-654, 2015.
   代码：C++, Python
   10.Jing Tang, Xueyan Tang, Xiaokui Xiao, Junsong Yuan, “Online Processing Algorithms for Influence Maximization,” in Proc. ACM SIGMOD, 2018.
   代码：C++, C
10. A. O. Saritac, A. Karakurt and C. Tekin, “Online contextual influence maximization in social networks”, in Proc. 54th Allerton Conference, September 2016, Monticello, Illinois.
    代码：Python, C, C++
11. Online content-aware influence maximization
    代码：Python
12. Online Influence Maximization with Local Observations
    代码：Python
13. X. He and D. Kempe, “Robust influence maximization”, Proc. ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, pp. 885-894, 2016.
    代码：Python
    类似的关于Robust的代码：
    • Evaluate-the-Robustness-of-Influence-Maximization-Against-Edge-Uncertainty，上海交通大学项目Python
    • Package for solving a robust version of the influence maximization problem.Python
14. A. Gionis, E. Terzi and P. Tsaparas, “Opinion maximization in social networks”, Proc. SIAM Int Conf Data Mining, pp. 387-395, 2013.
    代码：MATLAB
    类似的关于Opinion maximization的代码：
    • Maximizing Contrasting Opinions in Signed Social NetworksPython
15. 未知论文：Influence-propagation-over-social-network
    代码：Java