帝国竞争算法(Imperialist Competitive Algorithm, ICA)

帝国竞争算法(Imperialist Competitive Algorithm, ICA)

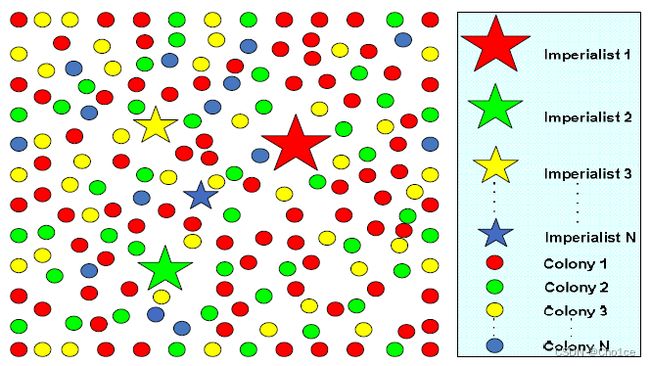
      本文提出了一种受帝国主义竞争启发的优化算法。与其他进化算法一样，该算法从初始种群开始。被称为国家的人口有两种类型：殖民地和宗主国，他们都来自某些帝国。这些帝国之间的帝国竞争构成了所提出的进化算法的基础。在这场竞争中，弱小的帝国崩溃，强大的帝国占领了它们的殖民地。帝国竞争最终汇聚到一个只有一个帝国的国家，它的殖民地与宗主国处于同样的地位，拥有同样的代价函数值。将该算法应用于一些基准代价函数，表明了其处理不同类型优化问题的能力。

帝国竞争算法流程图如下图：

1、初始化帝国

1.1 制定规则

在一个$N_{var}$维优化问题中，一个国家即为一个$1\ast N_{var}$的矩阵，国家可以表示成如下形式：

$country=[p_1,p_2,p_3,\dots ,p_{N_{var}}]$

此处$p_i$为被优化的变量，这些在国家属性中的变量是浮点数。国家中的每个变量可以被理解为这个国家的社会政治属性。国家的实力大小由代价函数来衡量。代价函数表示如下：

$cost=f(country)=f(p_1,p_2,p_3,\dots ,p_{N_{var}})$

国家的势力和代价函数值成反比，即代价函数值越小，国家势力越大。该算法即是要求我们寻找到最小的代价函数函数值。

1.2 初始化

$Step1$ 首先随机生成$N_{pop}$ 个国家作为初始群体。根据各国家的代价函数值选取势力较大的前 $N_{imp}$ 个作为宗主国，剩下的 $N_{col}$ 个国家作为殖民地。殖民地个数为：

$N_{col}=N_{pop}-N_{imp}$

$Step2$ 一个帝国由一个宗主国及多个殖民地组成，根据各个宗主国的势力大小确定殖民地的归属。即：一个帝国集团最初拥有的殖民地数量应直接与其力量所占比例相关。为了能按比例分配殖民地，每个帝国的标准化代价函数值被定义为：

$C_n=c_n-max\{c_i\}$

在这里，$c_n$为第$n$个帝国的代价函数值，$max\{c_i\}$是所有帝国的势力最大值。

计算了所有帝国的标准化代价函数值后，帝国的相对势力定义为：

$p_n=|\frac{C_n}{{\sum }_{i=1}^{N_{imp}}{C}_i}|$

最初的殖民地的分配依赖于其所属的帝国集团的力量。从而最初的殖民地分配为：

$N.C{.}_n=round\{p_n\ast N_{col}\}$

$round$是一个将小数四舍五入成整数的函数。

$Step3$ 从$N_{col}$个殖民地中随机选择相应的个数分配给各帝国，最终形成初始的$N_{imp}$个帝国。

2、同化与反转机制

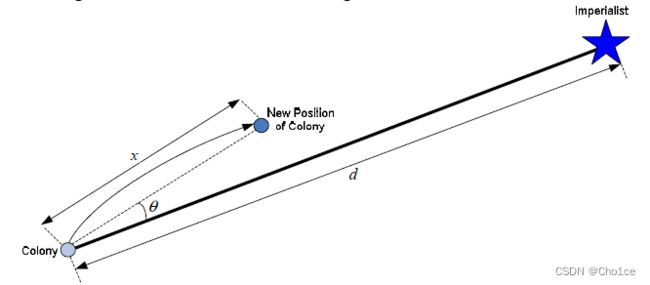
为了实现吸收壮大的目的，帝国试图去吸收它们的殖民地并使其成为帝国的一部分。宗主国对殖民地进行改善和思想控制，即同化作用。通过所有殖民地国家向其所属宗主国移动来模拟同化过程。更准确的说，殖民地沿着坐标轴向着帝国移动。移动过程如图$3$所示。考虑一个二维最优化问题，殖民地在由文化和语言组成的二维坐标轴中被帝国吸收。殖民地将会不断地向宗主国移动，最终将使殖民地完全被帝国吸收。

殖民地向帝国主义国家移动的距离$x$定义如下：

$x\sim U(0,\beta \times d)$

其中，$\beta ＞1$，殖民地可以从两个方向朝宗主国靠近；$d$是殖民地和宗主国之间的距离，随机变量$x$服从$(0,\beta \times d)$上的均匀分布。

同化公式表示为：

$\{X{\}}_{new}=\{X{\}}_{old}+U(0,\beta \times d)\times \{V\}$

其中$\{V\}$表示殖民地指向所属宗主国的方向向量。

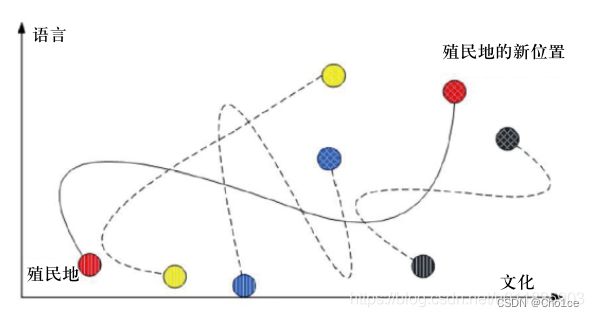
为了在帝国主义国家周围寻找不同的点，扩大寻找范围，算法增加了革命的概念。革命是指在力量和组织结构的基础方面在相对短时间内发生变化。革命使一个国家的社会政治特征突然产生变化。即，与帝国的吸收不同，殖民地是随机的在社会政治坐标轴中突然发生位置上的改变。图$4$和图$5$是在文化语言坐标轴中的革命过程。这种革命增加了该算法的搜索过程同时组织了国家形成早期的局部收敛。

算法中的革命率显示的是每个殖民地随机改变它们位置的比例。一个较高的革命率会降低算法的搜索效果并降低收敛率。在我们的应用中，我们将革命率设定为$0.3$。 即，是指帝国集团中有$30\%$的殖民地会随机改变它们的位置。

在同化基础上，增加了一个随机偏离方向$\theta$，定义如下：

$\theta \sim U(-\gamma ,\gamma )$

其中，$0<\gamma <\pi$。(大多应用中$\beta$常取$2$，$\gamma$常取$\pi /4$)


在殖民地向宗主国移动的过程中，殖民地的位置发生更新，可能出现某个殖民地的代价函数值比宗主国小的情况，即该殖民地的势力更大。此时，将该殖民地与宗主国的角色进行交换，即该殖民地成为该国家的宗主国，而原来的宗主国则沦为殖民地。而后，算法将由在新位置的帝国吸收新位置的殖民地过程继续下去。如图$6$所示为帝国和殖民地交换位置的过程。在该图中，最好的殖民地由深色表示，该殖民地比其宗主国的成本要小。如图 7 所示为殖民地和宗主国交换位置后的状态。


在殖民地和宗主国向着目标最小值移动的过程中，一些帝国可能会移动到相似的位置，如果两帝国之间的位置要小于初始位置，它们将会合并为一个新的帝国集团。原帝国集团的殖民地将会成为新帝国集团的殖民地，同时新帝国的位置将由原帝国中二者之一的位置所决定。图$8$和图$9$显示的合并过程。

3、帝国集团竞争

帝国竞争机制模拟的是现实社会中势力较强的帝国占有并控制势力较弱帝国的殖民地的过程。帝国之间的竞争导致强的帝国变得更强，而弱的帝国逐渐衰败。

$Step1$ 一个帝国集团的总势力主要由它的宗主国势力所决定。可是殖民地的势力也对帝国集团的势力有影响。一个帝国集团的总代价函数值由下式所决定：

$T.C{.}_n=Cost(imprialis{t}_n)+\xi mean\{Cost(coloniesofempir{e}_n)\}$

也即是：

$T.C{.}_n=f(im{p}_n)+\xi \times \frac{{\sum }_{i=1}^{N.C{.}_n}f(co{l}_i)}{N.C{.}_n}$

其中，$im{p}_n$是第$n$个帝国的宗主国，$T.C{.}_n$为第$n$个帝国集团的总代价。$\xi$是殖民地影响因子，为一个较小的正数。 其大小决定了殖民地国家对整个帝国势力的影响程度，且$0<\xi <\pi$。$\xi$越大会使殖民地对帝国集团的影响越大。在大部分的情况下$\xi$取$0.1$被认为是最好的。

$Step2$ 每个帝国集团都试图占领并控制其他帝国集团的殖民地。帝国竞争过程中，强国将更强，弱国将更弱。根据各帝国的总代价，选择最弱的帝国中最弱的殖民地作为帝国竞争的对象。在这个过程中，基于各自的力量，每个集团都有占领最弱集团的可能性。从另一个方面来说，最弱国不一定确定被最强国家占领，但是越强的集团占领弱集团的可能性越大。图$10$显示了帝国竞争的过程。

每个帝国占有最弱殖民地的概率按照如下公式计算：

$N.T.C{.}_n=T.C{.}_n-\underset{i}{\max }\{T.C.i\}$

此处，$T.C{.}_n$和$N.T.C.n$分别为第$n$个帝国集团的总代价和标准化总代价。

$Step3$ 依据标准化总代价，每个帝国的占领可能性由下式决定：

$P_{pn}=|\frac{N.T.C{.}_n}{{\sum }_{i=1}^{N_{imp}}N.T.C{.}_i}|$

为了将在帝国集团中将上述的殖民地分类，我们引入如下向量$P$：

$P=[P_{p1},P_{p2},P_{p3},...,P_{p_{N_{imp}}}]$

向量$R$是与向量$P$具有相同规格的向量，其元素服从均匀分布：

$R=[r_1,r_2,...,r_{N_{imp}}]$

$r1,r2,...,r_{N_{imp}}\sim U(0,1)$

向量$D$由向量$P$减去向量$R$所得：

$D=P-R=[D_1,D_2,D_3...,D_{N_{imp}}]=[p_{p_1}-r_1,p_{p_2}-r_2,p_{p_3}-r_3,...,p_{p_{N_{imp}}}-r_{N_{imp}}]$

显然，向量$D$中值越大，则对应帝国的势力越大。因此，最终应该将殖民地分配给向量$D$中最大值相应的帝国。

4、帝国灭亡，合并收敛

帝国之间的竞争，使势力大的帝国通过占有其他帝国的殖民地变得越来越强大，而势力弱的帝国殖民地个数不断减少。上述步骤将会持续下去直至实现国家收敛并且达到代价最小的目标。

不同标准可用来结束该算法。一种思想是设定最大迭代次数。或者当仅剩一个帝国集团时即结束该算法。

当使用仅剩一个帝国集团时即结束该算法时。即，当一个帝国丢失所有的殖民地时，帝国覆灭。随着帝国的灭亡，最终剩下一个帝国，此时算法终止。

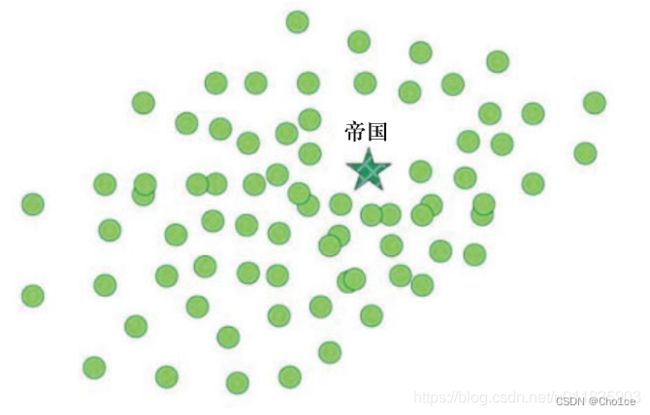
除了最强大的帝国之外，所有帝国都会崩溃，所有殖民地都将在这个独特的帝国的控制之下。在这个理想的新世界中，所有殖民地将拥有相同的地位和代价，并且将由以与自己相同的地位和代价的宗主国对其进行控制。在这个理想的世界中，不仅殖民地之间没有区别，而且殖民地与宗主国之间也没有区别。在这种情况下，我们结束了帝国主义竞争并停止了算法。

这样选择帝国集团的过程与遗传算法中选择母类的轮盘赌过程相似。但是这里的选择方法比相关的轮盘赌过程要快。因为这个过程并不需要计算累积分布函数，并且选择过程仅仅基于可能性的值。因此，帝国集团的选择过程可以完全替换遗传算法中的轮盘赌，并增加执行速度。

帝国主义算法流程简单描述如下：
$1)$ 选择函数上的一些随机点并初始化帝国；
$2)$ 将殖民地移向相应的宗主国（同化）；
$3)$ 如果一个帝国中有一个殖民地的代价函数值低于宗主国，那么就交换该殖民地和宗主国的地位
$4)$ 计算所有帝国的总代价函数值（宗主国及其殖民地）；
$5)$ 最弱的帝国中挑选最弱的殖民地，并将其交给最有可能占有它的帝国（帝国主义竞争）；
$6)$ 消灭最弱的帝国；
$7)$ 如果只有一个帝国，则停止；如果没有，则从步骤$2)$ 重新开始。

参考文献：

[1] Atashpaz-Gargari E, Lucas C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition[C]//2007 IEEE congress on evolutionary computation. Ieee, 2007: 4661-4667.

参考博客：

快速对帝国竞争算法ICA的了解

智能优化算法：帝国主义竞争算法-附代码