数据结构与算法09:二叉树
目录
【树】
【二叉树】
二叉树的遍历
Go代码实现
二叉树的复杂度分析
【二叉搜索树】
Go代码实现
【平衡二叉树】
2-3树
红黑树
【每日一练:移除元素】
【树】
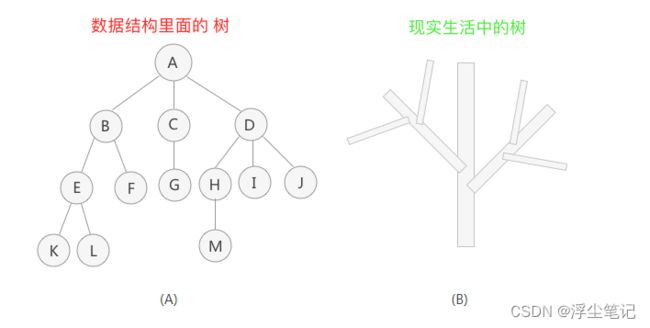
什么是树?这个不用解释了吧,马路两边种的都是树。数据结构里面的“树”和现实生活中的树类似,像一颗反过来的树,最上面是树根,下面是树的各个分枝,如下图所示:
树里面的每个元素叫作“节点”,最顶端的是“根节点”(图中A是根节点),上下层级的是“父子节点”(A是B、C、D的父节点),同一层级的是“兄弟节点”(B、C、D之间是兄弟节点),最后一层是“叶子结点”(K、L、F、G、M、I、J是叶子结点)。
关于树的高度、深度、层数:
- 节点的高度:节点到叶子节点的最长路径(边数)
- 节点的深度:根节点到这个节点所经历的边的个数
- 节点的层数:节点的深度 + 1
- 树的高度:根节点的高度
【二叉树】
在各种各样的树中,最常用的是二叉树,每个节点最多有两个子节点,分别是左子节点和右子节点,二叉树并不要求每个节点都有两个子节点,有的只有左子节点,有的节点只有右子节点。
同理,如果每个节点有四个节点的树就是“四叉树”,有八个节点的树就是“八叉树”。
要存储一棵二叉树,可以选择基于指针的二叉链式存储法,也可以选择基于数组的顺序存储法。
链式存储的二叉树:每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针,只要拎住根节点就可以通过左右子节点的指针把整棵树都串起来。大部分二叉树代码都是通过链式结构来实现的。
数组存储的顺序二叉树:把根节点存储在 i 的位置,左子节点就存储在 i * 2 的位置,右子节点就存储在 i * 2 + 1 的位置;反过来,下标为 i/2 的位置存储的就是对应的父节点。通过这种方式,只要知道根节点存储的位置(为了方便计算子节点,根节点会存储在下标为 1 的位置),就可以通过下标计算把整棵树都串起来。
二叉树又分为:普通二叉树、满二叉树、完全二叉树、非完全二叉树等。
满二叉树:叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点。
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。最后一层叶子结点靠左排列,是为了使用数组存储的时候不浪费太多空间。比如把上面的顺序二叉树改为非完全二叉树,就会出现浪费数组空间的情况。
二叉树的遍历
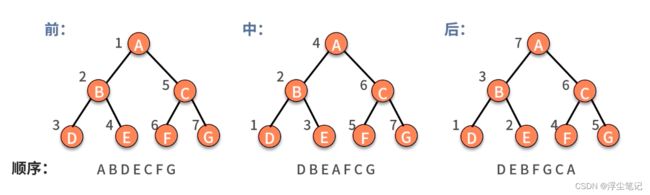
遍历二叉树的三种方法:前序遍历、中序遍历、后序遍历,这里的“序”指的是根节点的遍历顺序。
-
前序遍历:先遍历根节点,然后遍历左子树,最后遍历右子树(根->左->右)。print(r) => foreach(r->left) => foreach(r->right);
-
中序遍历:先遍历左子树,然后遍历根节点,最后遍历右子树(左->根->右)。foreach(r->left) => print(r) => foreach(r->right);
-
后序遍历:先遍历左子树,然后遍历右子树,最后遍历根节点(左->右->根)。foreach(r->left) => foreach(r->right) => print(r);
二叉树的前中后序遍历
//二叉树的前、中、后序 遍历的伪代码
//前序遍历
void preOrder(Node* root) {
if (root == null) return;
print root //打印root节点
preOrder(root->left); //打印左子树
preOrder(root->right); //打印右子树
}
//中序遍历
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left); //打印左子树
print root //打印root节点
inOrder(root->right); //打印右子树
}
//后序遍历
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left); //打印左子树
postOrder(root->right); //打印右子树
print root //打印root节点
}另外还可以对二叉树层序遍历:先遍历根节点,然后对于子节点中同一级的兄弟节点依次遍历,可以使用FIFO队列。
Go代码实现
下面是Go语言实现二叉树遍历的代码:
package main
import "fmt"
type BinaryTree struct {
Value int
LeftNode *BinaryTree
RightNode *BinaryTree
}
// 前序遍历: 根节点 ---> 左子树 ---> 右子树
func preOrder(node *BinaryTree) {
if node == nil {
return
}
fmt.Printf("%v ", node.Value)
preOrder(node.LeftNode)
preOrder(node.RightNode)
}
// 中序遍历: 左子树---> 根节点 ---> 右子树
func inOrder(node *BinaryTree) {
if node == nil {
return
}
inOrder(node.LeftNode)
fmt.Printf("%v ", node.Value)
inOrder(node.RightNode)
}
// 后序遍历: 左子树 ---> 右子树 ---> 根节点
func tailOrder(node *BinaryTree) {
if node == nil {
return
}
tailOrder(node.LeftNode)
tailOrder(node.RightNode)
fmt.Printf("%v ", node.Value)
}
// 层序遍历,从root节点一层一层的遍历
func levelOrder(rootNode *BinaryTree) {
if rootNode == nil {
return
}
var nodeSlice []*BinaryTree // 封装一个slice
nodeSlice = append(nodeSlice, rootNode)
recursion(nodeSlice) //递归遍历
}
// 递归遍历核心
func recursion(nodeSlice []*BinaryTree) {
if len(nodeSlice) == 0 { // 如果当前层级slice为空,则结束遍历
return
}
var nextSlice []*BinaryTree // 创建新的节点slice,存储下一层需要遍历的node
for i := 0; i < len(nodeSlice); i++ { //遍历当前nodeSlice
node := nodeSlice[i] //取出要遍历的node
fmt.Printf("%v ", node.Value) //输出当前node的值
if node.LeftNode != nil { //当前node左子节点append到下一层nodeSlice中
nextSlice = append(nextSlice, node.LeftNode)
}
if node.RightNode != nil { //当前node右子节点append到下一层nodeSlice中
nextSlice = append(nextSlice, node.RightNode)
}
}
recursion(nextSlice) //递归遍历下一层的nodeSlice
}
func main() {
//测试
/*
1
/ \
2 3
/ \ \
4 5 6
*/
var rootNode = &BinaryTree{
Value: 1,
LeftNode: &BinaryTree{
Value: 2,
LeftNode: &BinaryTree{
Value: 4,
},
RightNode: &BinaryTree{
Value: 5,
},
},
RightNode: &BinaryTree{
Value: 3,
RightNode: &BinaryTree{
Value: 6,
},
},
}
//前序遍历
preOrder(rootNode) //1 2 4 5 3 6
//中序遍历
inOrder(rootNode) //4 2 5 1 3 6
//后序遍历
tailOrder(rootNode) //4 5 2 6 3 1
//层序遍历
levelOrder(rootNode) //1 2 3 4 5 6
}
二叉树的复杂度分析
- 二叉树遍历过程中,函数调用栈的深度和树的高度有关,所以空间复杂度是O(H),H为树的高度。
- 二叉树遍历过程中,每个结点都被访问了一次,所以二叉树遍历的时间复杂度是O(n)。
- 二叉树中添加和删除数据时,只需要通过指针建立连接关系就可以了,所以二叉树添加和删除操作的时间复杂度是O(1)。
【二叉搜索树】
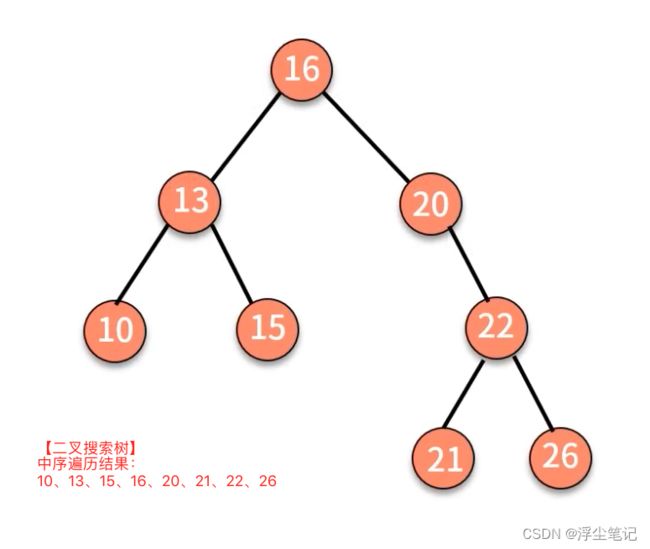
二叉搜索树又叫做 二叉查找树:在树中的任意一个节点,它的左子树中每个节点的值都要小于这个节点的值,右子树中每个节点的值都大于这个节点的值。也就是说以树的任意一个节点为分界线,左子树->当前节点->右子树 的数据由小到大。对二叉搜索树中序遍历后,可以输出一个从小到大的有序数据队列,时间复杂度是 O(n),非常高效。
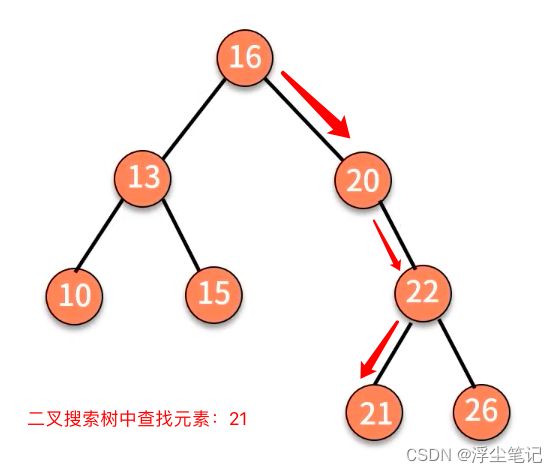
二叉搜索树的查找操作:
- 首先判断根结点是否等于要查找的数据,如果是就返回;
- 如果根结点大于要查找的数据,就在左子树中递归执行查找动作,直到查找到叶子结点;
- 如果根结点小于要查找的数据,就在右子树中递归执行查找动作,直到查找到叶子结点;
二叉搜索树的插入操作(需要先执行上面的查找操作,找到对应位置后再插入元素):
- 新插入的数据一般都是在叶子节点上,因此只需要从根节点开始依次比较要插入的数据和节点的大小关系。
- 如果要插入的数据比节点数值大,并且节点的右子树为空,就将新数据插入到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。
- 如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
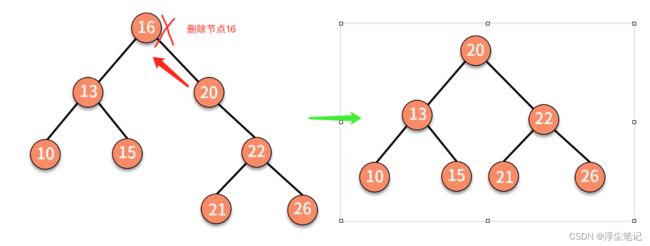
二叉搜索树的删除操作:
- 如果要删除的节点没有子节点,那么直接将父节点中指向要删除节点的指针置为 null。
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),那么需要更新父节点中指向要删除节点的指针,让它指向要删除节点的子节点就可以了。
- 如果要删除的节点有两个子节点,需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上,然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),此时可以应用上面两条规则来删除这个最小节点。(也可以将要删除的节点标记为“已删除”,但并不真正从树中将这个节点去掉,会比较浪费内存空间)
Go代码实现
下面是Go语言实现二叉搜索树的代码:
package main
import (
"fmt"
)
// 二叉查找树根节点
type BinarySearchTree struct {
Root *BinarySearchTreeNode // 树根节点
}
// 二叉查找树节点
type BinarySearchTreeNode struct {
Value int64 // 值
Times int64 // 值出现的次数
Left *BinarySearchTreeNode // 左子树
Right *BinarySearchTreeNode // 右字树
}
// 初始化一个二叉查找树
func NewBinarySearchTree() *BinarySearchTree {
return new(BinarySearchTree)
}
// 添加元素
func (tree *BinarySearchTree) Add(value int64) {
// 如果没有树根,证明是颗空树,添加树根后返回
if tree.Root == nil {
tree.Root = &BinarySearchTreeNode{Value: value}
return
}
// 将值添加进去
tree.Root.Add(value)
}
func (node *BinarySearchTreeNode) Add(value int64) {
if value < node.Value { // 如果插入的值比节点的值小,那么要插入到该节点的左子树中
if node.Left == nil { // 如果左子树为空,直接添加
node.Left = &BinarySearchTreeNode{Value: value}
} else { // 否则递归
node.Left.Add(value)
}
} else if value > node.Value { // 如果插入的值比节点的值大,那么要插入到该节点的右子树中
if node.Right == nil { // 如果右子树为空,直接添加
node.Right = &BinarySearchTreeNode{Value: value}
} else { // 否则递归
node.Right.Add(value)
}
} else { // 值相同,不需要添加,值出现的次数加1即可
node.Times = node.Times + 1
}
}
// 查找指定节点
func (tree *BinarySearchTree) Find(value int64) *BinarySearchTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.Find(value)
}
func (node *BinarySearchTreeNode) Find(value int64) *BinarySearchTreeNode {
if value == node.Value {
// 如果该节点刚刚等于该值,那么返回该节点
return node
} else if value < node.Value {
// 如果查找的值小于节点值,从节点的左子树开始找
if node.Left == nil {
// 左子树为空,表示找不到该值了,返回nil
return nil
}
return node.Left.Find(value)
} else {
// 如果查找的值大于节点值,从节点的右子树开始找
if node.Right == nil {
// 右子树为空,表示找不到该值了,返回nil
return nil
}
return node.Right.Find(value)
}
}
// 删除指定的元素
func (tree *BinarySearchTree) Delete(value int64) {
if tree.Root == nil {
// 如果是空树,直接返回
return
}
// 查找该值是否存在
node := tree.Root.Find(value)
if node == nil {
// 不存在该值,直接返回
return
}
// 查找该值的父亲节点
parent := tree.Root.FindParent(value)
// 第一种情况,删除的是根节点,且根节点没有儿子
if parent == nil && node.Left == nil && node.Right == nil {
// 置空后直接返回
tree.Root = nil
return
} else if node.Left == nil && node.Right == nil {
// 第二种情况,删除的节点有父亲节点,但没有子树
// 如果删除的是节点是父亲的左儿子,直接将该值删除即可
if parent.Left != nil && value == parent.Left.Value {
parent.Left = nil
} else {
// 删除的原来是父亲的右儿子,直接将该值删除即可
parent.Right = nil
}
return
} else if node.Left != nil && node.Right != nil {
// 第三种情况,删除的节点下有两个子树,因为右子树的值都比左子树大,那么用右子树中的最小元素来替换删除的节点,这时二叉查找树的性质又满足了。
// 找右子树中最小的值,一直往右子树的左边找
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 把最小的节点删掉
tree.Delete(minNode.Value)
// 最小值的节点替换被删除节点
node.Value = minNode.Value
node.Times = minNode.Times
} else {
// 第四种情况,只有一个子树,那么该子树直接替换被删除的节点即可
// 父亲为空,表示删除的是根节点,替换树根
if parent == nil {
if node.Left != nil {
tree.Root = node.Left
} else {
tree.Root = node.Right
}
return
}
// 左子树不为空
if node.Left != nil {
// 如果删除的是节点是父亲的左儿子,让删除的节点的左子树接班
if parent.Left != nil && value == parent.Left.Value {
parent.Left = node.Left
} else {
parent.Right = node.Left
}
} else {
// 如果删除的是节点是父亲的左儿子,让删除的节点的右子树接班
if parent.Left != nil && value == parent.Left.Value {
parent.Left = node.Right
} else {
parent.Right = node.Right
}
}
}
}
// 中序遍历
func (tree *BinarySearchTree) MidOrder() {
tree.Root.MidOrder()
}
func (node *BinarySearchTreeNode) MidOrder() {
if node == nil {
return
}
// 先打印左子树
node.Left.MidOrder()
// 按照次数打印根节点
for i := 0; i <= int(node.Times); i++ {
fmt.Print(node.Value, " ")
}
// 打印右子树
node.Right.MidOrder()
}
func main() {
values := []int64{3, 6, 8, 20, 9, 2, 6, 8, 9, 3, 5, 40, 7, 9, 13, 6, 8}
// 初始化二叉查找树并添加元素
tree := NewBinarySearchTree()
for _, v := range values {
tree.Add(v)
}
fmt.Println(tree.Root.Value) //3
// 查找存在的9
node = tree.Find(9) //true
// 删除存在的9后,再查找9
tree.Delete(9)
node = tree.Find(9) //false
// 中序遍历,实现排序
tree.MidOrder() //2 3 3 5 6 6 6 7 8 8 8 13 20 40
}Golang二叉树源代码:https://gitee.com/rxbook/go-algo-demo/tree/master/tree
关于PHP中对二叉树的遍历,参考:PHP二叉树1 和 PHP二叉树2
【平衡二叉树】
二叉搜索树支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下的时间复杂度是 O(logn)。因为比当前节点大的元素一定在当前节点右边,反之则在当前节点左边,所以每次比较总可以排除左右子树中的一颗。但是在某些极端情况下二叉搜索树可能会退化成一个有序链表,时间复杂度也会退化到O(n),比如下面这样:
为了能够更加高效的使用二叉搜索树,就要将二叉搜索树的左子树和右子树设计的尽可能平衡,也就是:平衡搜索树。
二叉树中任意一个节点的左右子树的高度相差不能大于 1 的时候就是平衡二叉树,完全二叉树和满二叉树都是平衡二叉树,非完全二叉树也有可能是平衡二叉树。设计平衡二叉树是为了解决普通二叉搜索树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化为O(n)链表的问题。
平衡二叉树中“平衡”的意思,就是让整棵树左右看起来比较对称和平衡,不要出现左子树或右子树一边很高,另一边很矮的情况,这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率也高一些。
2-3树
2-3树是平衡搜索树中的一种,就是除了普通的 2 节点之外还引入了一种 3 节点。其中2节点有一个键和两条链,分别链向左子树和右边子树;3节点在2节点的基础上增加了一个键,构成了一个有两个键和三条链的结构。如下图所示,左链指向了小于5的节点,右链指向了大于10的节点,中间的区域是5和10之间的节点。由于2-3树实现起来比较复杂,因此没有被广泛应用。
红黑树
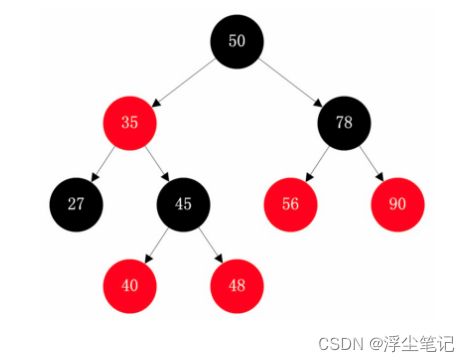
平衡二叉搜索树中比较常见的是“红黑树”(Red-Black Tree),红黑树中的节点要么是黑色,要么是红色,如下图所示:
关于红黑树有以下特点:
-
红黑树的根节点是黑色的;
-
任何相邻的节点都不能同时为红色,红色节点是被黑色节点隔开的;
-
从任意一个节点到达它的任意一个叶子节点的所有路径中的黑色节点数量相等;
-
每个叶子节点都是黑色的空节点,叶子节点不存储数据;
红黑树只是做到了近似平衡,并不是严格的平衡,它的插入、删除、查找各种操作的时间复杂度基本上都是 O(logn)。 关于红黑树的细节实现稍微有点复杂,等后面有时间了我再详细分析。
【每日一练:移除元素】
力扣27. 移除元素(源代码:leetcode/RemoveElement.go · 浮尘/go-algo-demo - Gitee.com)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
示例 1:输入:nums = [3,2,2,3], val = 3,输出:2, nums = [2,2]
示例 2:输入:nums = [0,1,2,2,3,0,4,2], val = 2,输出:5, nums = [0,1,3,0,4]
思路:要求原地修改数组,就不能开辟新的空间,分析如下:
- 循环遍历一次当前数组(切片),如果当前元素的值不等于 val ,就把当前元素的值重新赋值给当前数组从零开始的下标;
- 全部遍历一遍之后,所有等于val 的元素全都排到了数组的后面,然后直接返回已重新赋值的切片长度的子切片即可;
- 数组中的每个元素最多需要校验一次就可以了,因此时间复杂度是 O(N),空间复杂度: O(1)。
package main
import "fmt"
func removeElement(nums []int, val int) (int, []int) {
ret := 0
//把nums[0:ret]当做新数组,把nums数组中不等于val的元素覆盖的插入到里面
for i := 0; i < len(nums); i++ {
if nums[i] != val {
nums[ret] = nums[i]
ret++
}
}
// 返回新的数组中已经重新赋值过的长度,后面的都是传入的val
return ret, nums[0:ret]
}
func main() {
fmt.Println(removeElement([]int{3, 2, 2, 3}, 3)) //2 [2 2]
fmt.Println(removeElement([]int{0, 1, 2, 2, 3, 0, 4, 2}, 2)) //5 [0 1 3 0 4]
}