【计算机组成原理】乘法运算

原码乘法运算

r进制乘法可以将乘数变为，第k位数字乘r^k。
被乘数变为一个整数乘r^x。

Ex：

首先需要把0.1101分解为：1101 x 2^-4
然后将乘数0.1011分解为：1 x 2^-1 + 0 x 2^-2 + 1 x 2^-3 + 1 x 2^-4
最后将其相乘后相加
0.1101 x 0.1011 = (1101 x 1 x 2^-5) + (1101 x 0 x 2 ^-6) + (1101 x 1 x 2^-7) + (1101 x 1 x 2^-8) = 0.10001111
乘2^k 使用移位运算实现。

1、符号位如何处理
答：对两个符号位使用异或。
2、乘积位数扩大一倍如何处理
答：使用两个位数相同的寄存器存取数据
3、位积如何保存下来统一相加？X
答：不统一相加

原码一位乘法

每次加0或被乘数的绝对值补码
机器字长为n+1=5位（含一位符号位）
[x]_原 = 1.1101
[y]_原 = 0.1011

符号位单独运算：
1 异或 0 的结果为1。
数值位取绝对值计算：

[|x|]_原 = 0.1101
[|y|]_原 = 0.1011

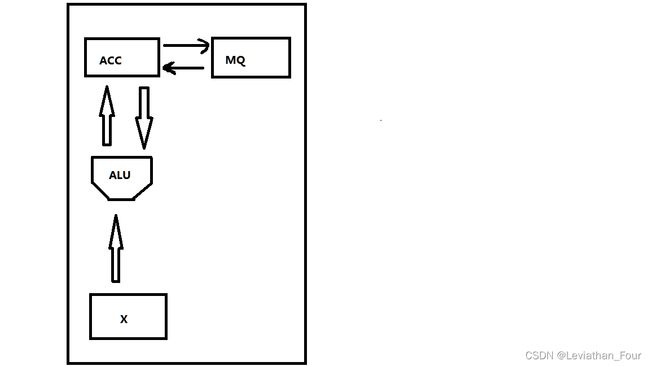
ACC(Accumulator):累加器，存放操作数，或运算结果
MQ(Multiple-Quotient Register):乘商寄存器，在乘除运算中存储操作数或运算结果
X(Arithmetic and Logic Unit):通用的操作数寄存器，用于存放操作数
ALU：算术逻辑单元，实现算术和逻辑运算

	+	-	x	/
ACC	被加数、和	被减数、差	乘积高位	被除数、余数
MU			乘数、乘积低位	商
X	加数	减数	被乘数	除数

实现方法：先加法再移位，高位补0，舍弃MQ最后一位，n次（n为乘数数值位长度）

ACC置0，MQ为乘数，X为被乘数。

若当前MQ最后一位为1，在ACC上加被乘数，然后向右移位。
若当前MQ最后一位为0，在ACC上加0，然后向右移位。
注意小数点位置。
最后修改符号位，ACC第一位为符号位。

若采用一位符号位：
ACC 为n+1位 ：第一位最后为符号位
MQ为n+1位：存放乘数包括其符号位，最后符号位不参与运算
X为n+1位：存放被乘数，包括其符号位

若采用两位符号位（手写二进制乘法）：
ACC 为n+2位 ：前两位最后为符号位
MQ为n位：存放乘数的数值位
X为n+2位：存放被乘数及其符号位，前两位为符号位。

两位符号位手算：

[x]_原 = 1.1101
[y]_原 = 0.1011

1、符号位异或得1为正数。
2、对两个数值的绝对值进行计算，n为4，4次乘法。
[|x|]_原 = 0.1101
[|y|]_原 = 0.1011

# 初始，ACC置0，MQ为乘数，X为被乘数
ACC 00.0000 MQ 1011
X      00.1101 
# 第一次加法
ACC加被乘数
ACC 00.1101 MQ 1011
X      00.1101 
ACC MQ 右移
ACC 00.0110 MQ 1101
X      00.1101 
# 第二次加法
ACC加被乘数
ACC 01.0011 MQ 1101
X      00.1101 
ACC MQ 右移
ACC 00.1001 MQ 1110
X      00.1101
# 第三次加法
ACC加0
ACC 00.1001 MQ 1110
X      00.1101 
ACC MQ 右移
ACC 00.0100 MQ 1111
X      00.1101
# 第四次加法
ACC加被乘数
ACC 01.0001 MQ 1111
X      00.1101 
ACC MQ 右移
ACC 00.1000 MQ 1111
X      00.1101
# 得到结果为ACC和MQ中的高位和低位前后相加，然后加上符号
00.1000 1111 + 符号位1
1.1000 1111

补码的乘法运算

补码一位乘法 & Booth算法

设计器字长为5位，数值位4位，符号位1位。x= -0.1101，y=+0.1011
补码一位乘法进行n轮加法和移位，最后再来一次加法。

与原码乘法不同，MQ的后方添加了一个辅助位。 辅助位初始为0。
由于计算机中寄存器的位数相同，ACC和X也是n+2位。因此采用双符号位。
每次加0、被乘数补码或被乘数相反数的补码

1、每次ACC如何加

#这里☞的最低位不是MQ的第n+2位，而是n+1位。
辅助位 - MQ最低位 = 1 时 ACC +　[x]_补
辅助位 - MQ最低位 = ０ 时 ACC +　０
辅助位 - MQ最低位 = －1 时 ACC +　[－x]_补

2、每次ACC如何移动

符号位不动，数值位右移，正数补0，负数补1。
ACC n+2位，MQ n+2位
X n+2位

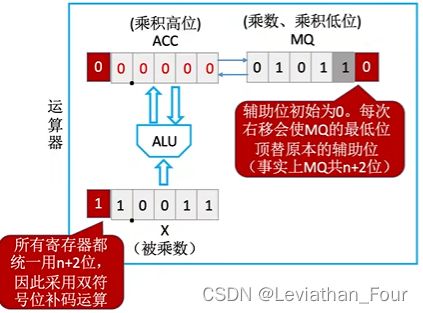
　设机器字长为5位，（含一位符号位，n=4）x=-0.1101，y=+0.1011
[x]_补 = 11.0011 ， [-x]_补 = 00.1101
[y]_补 = 00.1011

# 初始 ACC置0 MQ 为乘数 X为被乘数
ACC 00.0000 MQ 0.1011|0
X      00.1101
# 第一次加法，ACC加[-x]补码
ACC 00.1101 MQ 0.1011|0
X      00.1101
# ACC MQ右移
ACC 00.0110 MQ 10.101|10
X      00.1101
# 第二次加法，ACC加0
ACC 00.0110 MQ 10.101|10
X      00.1101
# ACC MQ 右移
ACC 00.0011 MQ 010.10|110
X      00.1101
# 第三次加法，ACC加[x]补码
ACC 11.0110 MQ 010.10|110
X      00.1101
# ACC MQ 右移
ACC 11.1011 MQ 0010.1|0110
X      00.1101
# 第四次加法，ACC加[-x]补码
ACC 00.1000 MQ 0010.1|0110
X      00.1101
# ACC MQ 右移
ACC 00.0100 MQ 00010.|10110
X      00.1101 
！# 第五次加法，ACC加[x]补码
ACC 11.0111 MQ 00010.|10110
X      00.1101 
第 n+1次没有移位！！！
最后结果的补码为
11.01110001
转为原码为
11.10001111
数值为
-0.10001111	

总结

原码和补码的乘法运算

	原码	补码
步骤比较	n次加法，n次移位	n+1次加法，n次移位
加数比较	+0、+[|x|]原	+0、+[x]补、+[-x]补
移位	逻辑右移（符号位不参与运算）、移位补0	算数右移（符号位参与运算）、移位补当前符号

原码加数和补码加数

原码MQ情况	原码ACC加数	补码MQ情况	原码ACC加数
最低为为0	+0	辅助位-MQ最低位 为1	+[x]补
最低位为1	+[|x|]原	辅助位-MQ最低位 为0	+0
		辅助位-MQ最低位 为-1	+[-x]补