学习笔记(十三):基于呼吸监测的人员计数和身份识别
2020《Respiration Tracking for People Counting and Recognition》读书笔记
本文在人群数量未知和被测人群呼吸速率相近的情况下,实现连续跟踪多人的呼吸速率,并利用估计的呼吸频率实现准静态场景下的身份匹配。主要通过以下技术实现了多人呼吸速率监测:
- 自适应子载波组合方法(提高呼吸信号信噪比)
- 迭代动态规划算法(连续跟踪多个呼吸波形-不同用户的呼吸速率序列)
- 轨迹拼接算法(实时连续跟踪多个用户呼吸率)
- 呼吸波形数据库和假设检验方法(智能家居场景的身份识别)
实验结果,四人及四人以下的计数中平均准确率可达到86%。在97.9%的测试案例中,人群数量估计的绝对误差小于1。该系统在智能家居案例中的人物识别平均准确率达到85.78%
目录
- 1. 系统概述
- 2. 获取多用户呼吸频谱
-
- 2.1 人体呼吸在CSI模型中的影响
- 2.2 提高人体呼吸信号的信噪比
-
- 2.2.1 利用STFT来从CSI中提取呼吸信号
- 3. 呼吸率时间轨迹
-
- 3.1 从呼吸速率时间集中得到呼吸率时间序列
- 3.2 从得到连续的呼吸率时间序列中区分出每个时间窗口中的每个人的呼吸率时间轨迹(IDP算法,待补充)
- 3.3 将连续时间窗上的每个人的呼吸率时间轨迹聚合(拼接算法,待补充)
- 4. 人数统计(基于分段的双边滤波器,待补充)
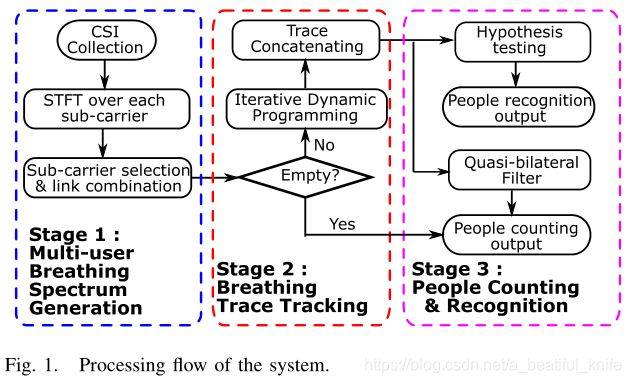
1. 系统概述
本文的重点是利用频域和时域信息进行身份匹配。核心思想是估计不同个体沿时间的呼吸速率序列(即呼吸速率波形)。
(1)获取多用户呼吸频谱
第一阶段,对CSI测量值短期傅立叶变换(STFT)以提取周期性呼吸信号。
依据:只要不同个体的呼吸频率不同,就会在频率响应中观察到多个频率分量。[引言里面说做到了呼吸频率相近的人体区分,这一点论文靠阶段二完成]
存在问题:提取的呼吸信号在单个SC上通常相当弱
问题解决方案:自适应SC组合方法进一步增强。
阶段(1)输出估计呼吸速率随时间变化的谱图
(2)呼吸速率跟踪
第二阶段,从呼吸速率-时间谱图中获得呼吸率轨迹(即呼吸源)。
存在问题:
- 不同的个体可能具有彼此重叠的相同呼吸频率
- 一个人的呼吸频率会随着时间而变化
实现方法: 引入了马尔可夫链模型,通过iterative dynamic programming (IDP)逐个获得每个个体的呼吸率轨迹。
(3)人数统计和识别
第三阶段,利用l呼吸率轨迹进行人数统计和识别。
做法:step1. 利用时域信息,通过准双边滤波器去除估计呼吸率轨迹的异常值,获得人群数量的估计。
step2. 通过假设检验,根据提取的呼吸频率轨迹进行人的身份识别。
2. 获取多用户呼吸频谱
2.1 人体呼吸在CSI模型中的影响
给定一对搭载全向天线的发射设备和接收设备,第m条链路在时间t何频率 f k f_k fk下,其CSI可建模为:
h ( m ) ( t , f k ) = ∑ l = 1 L a l ( t ) exp ( − j 2 π f k d l ( t ) c ) + n ( t , f k ) (1) h^{(m)}\left(t, f_{k}\right)=\sum_{l=1}^{L} a_{l}(t) \exp \left(-j 2 \pi f_{k} \frac{d_{l}(t)}{c}\right)+n\left(t, f_{k}\right)\tag{1} h(m)(t,fk)=l=1∑Lal(t)exp(−j2πfkcdl(t))+n(t,fk)(1)
其中, k ∈ V k \in \mathcal{V} k∈V是中心频率为 f k f_{k} fk的子载波的索引 V ⋅ L \mathcal{V} \cdot L V⋅L多径(multipath components ,MPCs)的总数。 a l ( t ) a_{l}(t) al(t) and d l ( t ) d_{l}(t) dl(t)分别是MPC l的复增益和传播路径长度. n ( t , f k ) n\left(t, f_{k}\right) n(t,fk)是加性高斯白噪声, c c c是光速。
当存在多人呼吸时,(1)式划分静动成分改写为:
h ( m ) ( t , f k ) = ∑ i ∈ I ∑ l ∈ Ω d i ( t ) a l ( t ) exp ( − j 2 π f k d l ( t ) c ) + ∑ l ∈ Ω s a l exp ( − j 2 π f d l c ) + n ( t , f k ) (2) \begin{aligned} h^{(m)}\left(t, f_{k}\right)=& \sum_{i \in \mathcal{I}} \sum_{l \in \Omega_{d_{i}}(t)} a_{l}(t) \exp \left(-j 2 \pi f_{k} \frac{d_{l}(t)}{c}\right) \\ &+\sum_{l \in \Omega_{s}} a_{l} \exp \left(-j 2 \pi f \frac{d_{l}}{c}\right)+n\left(t, f_{k}\right) \end{aligned}\tag{2} h(m)(t,fk)=i∈I∑l∈Ωdi(t)∑al(t)exp(−j2πfkcdl(t))+l∈Ωs∑alexp(−j2πfcdl)+n(t,fk)(2)
其中 I \mathcal{I} I是人数,第一部分表示人体导致的第l条动态多径对信道响应的贡献。
按《Wireless Communications》中观点,(2)式中的 a l ( t ) a_{l}(t) al(t)可写为(3)式:
a l ( t ) = a l × ( 1 + Δ d l d l sin θ sin ( 2 π t T b i + ϕ ) ) − Ψ (3) a_{l}(t)=a_{l} \times\left(1+\frac{\Delta d_{l}}{d_{l}} \sin \theta \sin \left(\frac{2 \pi t}{T_{b_{i}}}+\phi\right)\right)^{-\Psi}\tag{3} al(t)=al×(1+dlΔdlsinθsin(Tbi2πt+ϕ))−Ψ(3)其中 a l a_{l} al和 d l d_{l} dl分别是静态环境下的复增益和传播路径长度, Δ d l \Delta d_{l} Δdl是由胸部运动引起的传播长度的差异, θ \theta θ是人体散射方向和电磁波方向的夹角, ϕ \phi ϕ是初始相位, Ψ \Psi Ψ是路径损耗指数。
在仅有胸腔这一小幅度运动时, Ω d i ( t ) ≈ Ω d i \Omega_{d_{i}}(t) \approx \Omega_{d_{i}} Ωdi(t)≈Ωdi, Δ d l ≪ d l \Delta d_{l} \ll d_{l} Δdl≪dl,所以上式可简化为 a l ( t ) ≈ a l a_{l}(t) \approx a_{l} al(t)≈al,
2.2 提高人体呼吸信号的信噪比
对于每个人体对应的多径子集,由于人体周期性胸部运动,会使频域中测量的CSI有多个频率分量,每个频率分量对应于周期不同的呼吸信号。
2.2.1 利用STFT来从CSI中提取呼吸信号
首先对每个链路( N T x × N R x N_{\mathrm{Tx}} \times N_{\mathrm{Rx}} NTx×NRx)中的每个SC( N S c = 114 N_{\mathrm{Sc}}=114 NSc=114)上的CSI时间序列应用长度为W的滑动窗口,然后通过在每个时间窗口上执行快速傅立叶变换(FFT)来获得单个链路上单个SC的频谱。
然后,在频谱上使用带通滤波器,考虑正常范围的人类呼吸频率[bmin,bmax]。
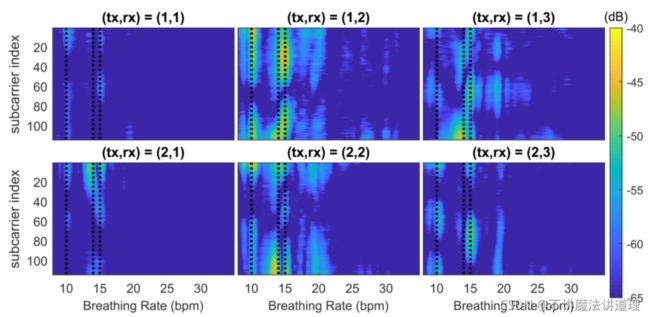
上图验证出:每个呼吸信号对所获得的功率谱密度(PSD,power spectrum density )贡献一个明显峰值。
该论文创新点(子载波筛选+链路等增益合并):
不同的SCs对相同的呼吸运动有不同的敏感度。以前的方法试图根据所有信号强度指标的方差、幅度或总体平均值来选择一组最佳信号强度指标,以提高信噪比。
本文提出一种新的自适应SC合并准则来提高每个环节呼吸信号的信噪比:
对于第m条链路,假设选定子载波SC包含呼吸频率成分q,q满足下式:
E k ( m ) ( q ) ≥ α max q ∈ Q , i ∈ V { E ( m ) ( q , i ) } ∀ k ∈ V E_{k}^{(m)}(q) \geq \alpha \max _{q \in Q, i \in \mathcal{V}}\left\{E^{(m)}(q, i)\right\} \quad \forall k \in \mathcal{V} Ek(m)(q)≥αq∈Q,i∈Vmax{E(m)(q,i)}∀k∈V 其中,Q是 [ b m i n , b m a x ] [b_{min},b_{max}] [bmin,bmax]范围内的频率分量集合, E k ( m ) ( q ) E_{k}^{(m)}(q) Ek(m)(q) 是链路m上的 k t h kth kth SC在频率q处对应的功率, m a x q ∈ Q , i ∈ V { E ( m ) ( q , i ) } max _{q \in Q, i \in \mathcal{V}}\left\{E^{(m)}(q, i)\right\} maxq∈Q,i∈V{E(m)(q,i)}是所有子载波的所有呼吸频率成分中的最大功率,其与阈值参数 α \alpha α共同确定上式左边的相对阈值 t h ( m ) t h^{(m)} th(m), t h ( m ) t h^{(m)} th(m)自适应于单个链路质量。
然后,根据阈值选出搭载了明显的每个人体产生的呼吸信号的SCs,对于第m条链路中频率q的呼吸频率成分功率有:
E ( m ) ( q ) ← ∑ k ∈ V E k ( m ) ( q ) 1 ( E k ( m ) ( q ) ≥ t h ( m ) ) E^{(m)}(q) \leftarrow \sum_{k \in \mathcal{V}} E_{k}^{(m)}(q) \mathbb{1}\left(E_{k}^{(m)}(q) \geq t h^{(m)}\right) E(m)(q)←k∈V∑Ek(m)(q)1(Ek(m)(q)≥th(m))
最后融合不同链路:对每个链路的功率进行归一化,然后将它们组合在一起 E ( m ) ( q ) ← E ( m ) ( q ) ∑ i ∈ Q E ( m ) ( i ) ∀ q ∈ Q E ( q ) ← ∑ m = 1 M E ( m ) ( q ) ∀ q ∈ Q \begin{aligned} &E^{(m)}(q) \leftarrow \frac{E^{(m)}(q)}{\sum_{i \in Q} E^{(m)}(i)} \quad \forall q \in Q \\ &E(q) \leftarrow \sum_{m=1}^{M} E^{(m)}(q) \quad \forall q \in Q \end{aligned} E(m)(q)←∑i∈QE(m)(i)E(m)(q)∀q∈QE(q)←m=1∑ME(m)(q)∀q∈Q该算法下,其呼吸率结果如下图所示,相比暴力平均,噪声和干扰已被有效抑制。
3. 呼吸率时间轨迹
3.1 从呼吸速率时间集中得到呼吸率时间序列
人体分辨存在难点:
1)不同用户的呼吸频率无法从频谱中分辨出来,导致潜在低估。
2)随着时间的推移,人数可能会有所不同,人体伴随的运动也会破坏呼吸信号。
创新点:
利用呼吸速率估计的时间序列的多样性来将呼吸速率映射到个体,从而进一步估计准确的人群数量。
1)将动态的呼吸率的数集建模为Markov过程:
可行性基础:呼吸信号周期性+呼吸频率随时间平滑变化
合理假设:相邻时间节点中的呼吸速率变化符合正态分布 N ( 0 , σ 2 ) \mathcal{N}\left(0, \sigma^{2}\right) N(0,σ2),其概率密度函数PDF为 p ( f ) p(f) p(f)
输入:从STFT中得到的频率在区间 [ b min , b max ] \left[b_{\min }, b_{\max }\right] [bmin,bmax]内的 ∣ Q ∣ |Q| ∣Q∣个频率成分
转移矩阵 P ∈ R ∣ Q ∣ × R ∣ Q ∣ \mathbf{P} \in \mathbb{R}^{|Q|} \times \mathbb{R}^{|Q|} P∈R∣Q∣×R∣Q∣:
P ( q , q ′ ) = P ( g ( i ) = q ′ ∣ g ( i − 1 ) = q ) = ∫ ( q ′ − q − 1 2 ) ∗ Δ f ( q ′ − q + 1 2 ) ∗ Δ f p ( f ) d f \begin{aligned} \mathbf{P}\left(q, q^{\prime}\right) &=\mathbf{P}\left(g(i)=q^{\prime} \mid g(i-1)=q\right) \\ &=\int_{\left(q^{\prime}-q-\frac{1}{2}\right) * \Delta f}^{\left(q^{\prime}-q+\frac{1}{2}\right) * \Delta f} p(f) \mathbf{d} f \end{aligned} P(q,q′)=P(g(i)=q′∣g(i−1)=q)=∫(q′−q−21)∗Δf(q′−q+21)∗Δfp(f)df其中 ∀ q , q ′ ∈ Q \forall q, q^{\prime} \in Q ∀q,q′∈Q,g是一个映射,表示在给定时隙的呼吸频率。
2)估计给定时隙t内的呼吸频率轨迹:
理论上可以利用[t-W,t]时间段的频谱,其中W是窗口长度。每隔 W s W_s Ws秒产生一个输出,同时更新频谱。利用频谱 S ∈ R + I × R + ∣ Q ∣ S \in \mathbb{R}_{+}^{I} \times \mathbb{R}_{+}^{|Q|} S∈R+I×R+∣Q∣(其中 I = ( W / W s ) I=\left(W / W_{s}\right) I=(W/Ws))表示t时刻的呼吸轨迹。
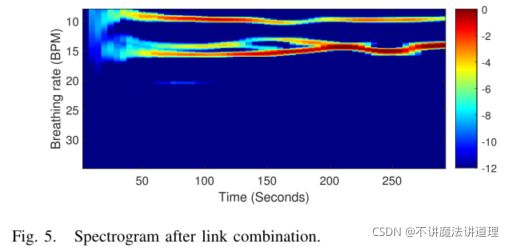
呼吸信号比噪声和其他运动干扰更具周期性。其在大部分时间在频谱上呈现峰值,因此呼吸信号将在给定频谱中随着频率稍微改变而沿着时间形成轨迹,如图5。
图5中,呼吸信号的能量围绕呼吸轨迹的中心扩散,这在给定的频谱中形成能量带
3.2 从得到连续的呼吸率时间序列中区分出每个时间窗口中的每个人的呼吸率时间轨迹(IDP算法,待补充)
3.3 将连续时间窗上的每个人的呼吸率时间轨迹聚合(拼接算法,待补充)
4. 人数统计(基于分段的双边滤波器,待补充)
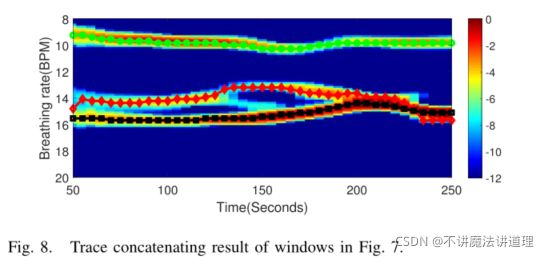
估计结果遭受噪声后可能对于如图7(b,c)所示的实时输出具有一些误报警或低估。为了减轻实时系统的这些异常值,利用准双边滤波器来探索包含在先前估计中的信息。
首先,对于实时系统,滤波器只能使用过去和当前的估计结果。此外,由于IDP和迹线拼接利用时间和频率信息来获得连续的呼吸频率迹线,所以初步估计在短时间内是一致的。
在去除人数估计的噪声后,引入假设检验进行人类身份识别。