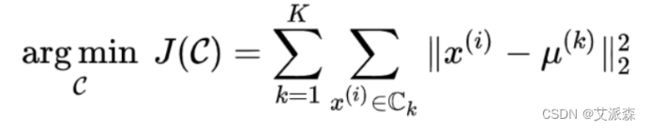KMeans+DBSCAN密度聚类+层次聚类的使用（附案例实战）

‍♂️ 个人主页：@艾派森的个人主页

✍作者简介：Python学习者
希望大家多多支持，我们一起进步！
如果文章对你有帮助的话，
欢迎评论 点赞 收藏 加关注+

---

目录

1.KMeans聚类算法

2.DBSCAN密度聚类算法

3.层次聚类

4.实战案例

4.1数据集介绍

4.2加载数据

4.3数据预处理 

4.4Kmeans聚类

4.5DBSCAN密度聚类

4.6层次聚类

4.7总结

文末福利

源代码

---

1.KMeans聚类算法

        kmeans聚类可以说是聚类算法中最为常见的，它是基于划分方法聚类的，原理是先初始化k个簇类中心，基于计算样本与中心点的距离归纳各簇类下的所属样本，迭代实现样本与其归属的簇类中心的距离为最小的目标（如下目标函数）。

其优化算法步骤为：

1.随机选择 k 个样本作为初始簇类中心（k为超参，代表簇类的个数。可以凭先验知识、验证法确定取值）；

2.针对数据集中每个样本 计算它到 k 个簇类中心的距离，并将其归属到距离最小的簇类中心所对应的类中；

3.针对每个簇类，重新计算它的簇类中心位置；

4.重复迭代上面 2 、3 两步操作，直到达到某个中止条件（如迭代次数，簇类中心位置不变等）。

关于具体的Kmeans介绍，可参考我之前博文

机器学习之KMeans聚类算法原理（附案例实战）

2.DBSCAN密度聚类算法

        BSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。它可以替代KMeans和层次聚类等流行的聚类算法。DBSCAN算法将“簇”定义为密度相连的点的最大集合。DBSCAN 算法中有两个重要参数：Eps 和 MmPtS。Eps 是定义密度时的邻域半径，MmPts 为定义核心点时的阈值。

DBSCAN聚类算法原理：

1、DBSCAN通过检查数据集中每个点的r邻域来搜索簇，如果点p的r邻域包含多于MinPts个点，则创建一个以p为核心对象的簇；

2、然后， DBSCAN迭代的聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并；

3、当没有新的带你添加到任何簇时，迭代过程结束。

DBSCAN算法的描述如下：

输入：数据集，邻域半径 Eps，邻域中数据对象数目阈值 MinPts;

输出：密度联通簇。

处理流程如下：

1）从数据集中任意选取一个数据对象点 p；

2）如果对于参数 Eps 和 MinPts，所选取的数据对象点 p 为核心点，则找出所有从 p 密度可达的数据对象点，形成一个簇；

3）如果选取的数据对象点 p 是边缘点，选取另一个数据对象点；

4）重复（2）、（3）步，直到所有点被处理。

注意：DBSCAN 算法的计算复杂的度为 O(n)，n 为数据对象的数目。这种算法对于输入参数 Eps 和 MinPts 是敏感的。

3.层次聚类

        层次聚类(Hierarchical Clustering)是通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。层次聚类算法分为两类：自上而下和自下而上。自下而上的算法在一开始就将每个数据点视为一个单一的聚类，然后依次合并类，直到所有类合并成一个包含所有数据点的单一聚类。

算法过程：

1.首先将每个数据点作为一个单个类，然后根据选择的度量方法计算两聚类之间的距离。

2.对所有数据点中最为相似的两个数据点进行组合，形成具有最小平均连接的组。

3.重复迭代步骤2直到只有一个包含所有数据点的聚类为止。

优点：

• 无需指定聚类的数量
• 对距离度量的选择不敏感
• 当底层数据具有层次结构时，可以恢复层次结构

缺点：时间复杂度为O(n³)

确定聚类数量：对于层次聚类，可以根据聚类过程中，每次合并的两个cluster的距离来作判断，取距离突变处的值为distance_threshold。若数据应当被分为K个簇，K个簇之间会有明显的间距。若合并的两个小簇同属于一个目标簇，那么它们的距离就不会太大。但当合并出来K个目标簇后，再进行合并，则是对K个簇间进行合并了，一般来说，此合并产生的距离就会有非常明显的突变。

4.实战案例

4.1数据集介绍

        本数据集是由249名度假者在2014年10月之前发布的目的地评论组成的。在整个南印度的目的地中，分为6类的评论被考虑，每个评论(旅行者)在每一类的评论计数被记录统计。数据集共有249条，共7列。具体字段信息如下表：

属性	数据类型	属性描述
User Id	Object字符类型	用户唯一的ID
Sports	Int整数类型	对体育场馆、体育综合体等的评论数量
Religious	Int整数类型	对宗教机构的评论数量
Nature	Int整数类型	关于海滩、湖泊、河流等的评论数量
Theatre	Int整数类型	关于剧院、展览等的评论数量
Shopping	Int整数类型	对商场、购物场所等的评论数量
Picnic	Int整数类型	对公园、野餐地点等的评论数量

4.2加载数据

 

4.3数据预处理 

4.4Kmeans聚类

首先使用肘部法则确定K

通过图形确定K值为3，使用Kmeans聚类 

 

4.5DBSCAN密度聚类

4.6层次聚类

4.7总结

        从前面结果中得到的三类聚类算法模型结果中，我们发现KMeans模型和层次聚类模型结果相似，而DBSCAN模型结果与KMeans模型和层次聚类模型结果差距较大。通过查阅相关资料，我们发现可能是在构建BDSCAN模型的时候，参数的选择很重要，参数变化一点点都会对最后的模型造成很大的影响，且由于本次数据集样本较少，对三个模型的结果都有一定的模型，样本数据过少会导致模型的泛化能力较差，不能很好的在实际应用中进行使用。

文末福利

参与福利 

• 抽奖方式：评论区随机抽取2位小伙伴免费送出！
• 参与方式：关注博主、点赞、收藏、评论区评论“人生苦短，拒绝内卷！”（切记要点赞+收藏，否则抽奖无效，每个人最多评论三次！）
• 活动截止时间：2023-06-05 20:00:00
•  京东自营店购买链接：https://item.jd.com/13737387.html#crumb-wrap

名单公布时间：2023-06-05 21:00:00   

源代码

import pandas as pd
import warnings
warnings.filterwarnings('ignore')
data = pd.read_csv('buddymove_holidayiq.csv')
data.head()
# 数据预处理
data.dropna(inplace=True)  # 删除缺失值
data.drop_duplicates(inplace=True)  # 删除重复值
# 数据标准化
from sklearn.preprocessing import StandardScaler
df = data.drop('User Id',axis=1)
scaler = StandardScaler()
X = scaler.fit_transform(df)
data_scaler = pd.DataFrame(X,columns=df.columns)
data_scaler.head()
KMeans聚类
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示|
plt.rcParams['axes.unicode_minus'] = False   #解决符号无法显示
from sklearn.cluster import KMeans
# 肘部法则
loss = []
for i in range(2,6):
    model = KMeans(n_clusters=i).fit(X)
    loss.append(model.inertia_)
    
plt.plot(range(2,6),loss)
plt.xlabel('k')
plt.ylabel('loss')
plt.show()
from sklearn.cluster import KMeans
k = 3 # 聚成3类
kmodel = KMeans(k)  # 创建聚类模型
kmodel.fit(data_scaler)  # 训练模型
print(pd.Series(kmodel.labels_).value_counts())
pd.Series(kmodel.labels_).value_counts().plot(kind='bar')
plt.title('KMeans聚类的结果')
plt.xlabel('聚类标签')
plt.ylabel('聚类数量')
plt.show()
DBSCAN密度聚类
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=1.1)
# 模型拟合
dbscan.fit(X)
data2 = data_scaler.copy()
data2['dbscan_label'] = dbscan.labels_
print(pd.Series(dbscan.labels_).value_counts())
data2['dbscan_label'].value_counts().plot(kind='bar')
plt.title('DBSCAN密度聚类的结果')
plt.xlabel('聚类标签')
plt.ylabel('聚类数量')
plt.show()
层次聚类
from sklearn.cluster import AgglomerativeClustering 
# n_clusters为集群数，affinity指定用于计算距离的度量，linkage参数中的ward为离差平方和法
Agg_hc = AgglomerativeClustering(n_clusters = 3, affinity = 'euclidean', linkage = 'ward')
y_hc = Agg_hc.fit_predict(data_scaler) # 训练数据
print(pd.Series(y_hc).value_counts())
pd.Series(y_hc).value_counts().plot(kind='bar')
plt.title('层次聚类的结果')
plt.xlabel('聚类标签')
plt.ylabel('聚类数量')
plt.show()