线性插值提高DDS相位分辨率

  DDS（Direct Digital Synthesizer）即直接数字频率合成技术，主要由正弦查找表与控制器组成，通过控制器给出的相位，在正弦查找表中查找对应的正余弦值并予以输出。通过多个 DDS 信号的组合，可以进一步构建出 AM、FM、PM 等信号发生器。

  关于 DDS 的知识不多赘述，本文主要介绍正弦波生成模块的 FPGA 实现，里面涉及一个在不增加 ROM 容量的情况下，大幅提高相位分辨率的方法（线性插值）。如果需要更高的精度，可以更进一步采用三次样条差值等技术。

生成 ROM 文件（正弦查找表）

  使用 Matlab 生成 .coe 文件（这个是 Xilinx 的 rom 需要的初始化文件，如果是 Altera 的板子，rom 需要用 .mif 文件），代码如下

%--------------生成正弦查找表.coe---------------------
clc,clear,close all

%% 生成 rom 数据
Width=16;
Depth=256;

phi=linspace(0,2*pi,Depth+1);
phi=phi(1:end-1)';

sin_sig=sin(phi);
sin_sig=floor(sin_sig*2^(Width-1)*0.9999); %*0.9999防止出现溢出
sin_sig=sin_sig+2^(Width-1);

plot(sin_sig)

%% 生成.coe文件
filename='.\sin_rom.coe';
fid = fopen(filename,'w');

radix = 16;
fprintf(fid,"memory_initialization_radix=%d;\n",radix); %使用的进制
fprintf(fid,"memory_initialization_vector=");

for i=1:size(sin_sig,1)
    fprintf(fid,"\n%x",sin_sig(i));
end
fprintf(fid,";");

fclose(fid);

正弦查找器

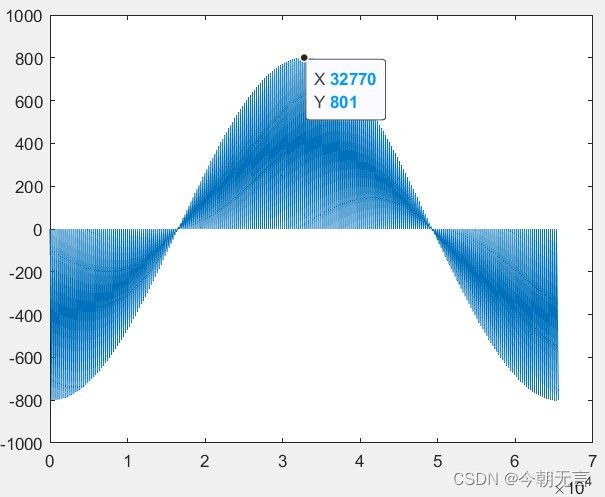
  一般为了节约 FPGA 资源，不会生成太大的 rom，为了保证幅度的精度，一般选取 16bit，而查找表深度一般选择 256，然而这就导致相位分辨率很低，如果直接使用这个 rom 的数据作为正弦信号输出，这个信号将是很不理想的。比如需要的相位分辨率为 T/65536，如果直接相位下取整作为 rom 地址，并输出对应的正弦数据，将会产生如下的误差

可以看到最大的误差将达到 $\pm 800$，这对于 $[-32768,32768]$ 的取值范围来说，相对误差达到了惊人的 $2.44\%$！即使采用改进方案，相位取整采取四舍五入，而不是下取整，误差也仅仅降低一半，仍有 $1.22\%$，在精度要求较高的场所这仍然是不可接受的。

  为提高相位分辨率，一种方法是直接生成更高相位分辨率的正弦查找表，而这将大大增加 FPGA 资源的消耗（想当年我就是用这种方法获取更高分辨率的，结果被资源耗尽的问题搞得焦头烂额（╥﹏╥），往事不堪回首啊 hhhh）。但如果采用两个 256 深度的查找表，一个按给定相位的下取整查找对应正弦信号的值，一个相位上取整查找，然后通过线性插值
$$y=y_1+(y_2-y_1)\frac{x-x_1}{x_2-x_1}$$
来计算，就可以获得给定相位处的高精度正弦值了。其中 $x_1$ 是 16bit 输入相位 $x$ 对 256 下取整的相位， $x_2$ 是输入相位 $x$ 对 256 上取整的相位，$x_2-x_1=256$，因此下面代码中除 256 就直接做了移位运算（右移 8 位），$y_1$ 是下取整相位的正弦查找值，$y_2$ 是上取整相位的正弦查找值，计算结果 $y$ 就是线性插值获得的正弦输出。

  采用线性差值的正弦信号发生器代码如下

/* 
 * file			: sin_gen.v
 * author		: 今朝无言
 * date			: 2023-05-16
 * version		: v1.0
 * description	: 根据给定相位输出正弦信号
 */
module sin_gen(
input			clk,

input	[15:0]	phase,		//相位，0~65535对应[0~2pi)
output	[15:0]	sin_out
);

//---------------------正弦查找表-------------------------
wire	[7:0]	addr1;
wire	[7:0]	addr2;
wire	[15:0]	sin_dat1;
wire	[15:0]	sin_dat2;

//sin rom, 16bit, 256 depth
sin_rom sin_rom_inst1(
	.clka	(clk),
	.addra	(addr1),
	.douta	(sin_dat1)
);

sin_rom sin_rom_inst2(
	.clka	(clk),
	.addra	(addr2),
	.douta	(sin_dat2)
);

//-----------线性插值获取更精确的相位分辨率-------------------
assign	addr1	= (phase>>8);
assign	addr2	= (phase>>8)+1;

wire	[15:0]	phase1;
wire	[15:0]	phase2;

assign	phase1	= addr1<<8;
assign	phase2	= addr2<<8;

reg		[15:0]	phase_d0;
reg		[15:0]	phase_d1;	//由于rom数据2拍后才给出，因此phase需要与之同步
reg		[15:0]	phase1_d0;
reg		[15:0]	phase1_d1;

always @(posedge clk) begin
	phase_d0	<= phase;
	phase_d1	<= phase_d0;

	phase1_d0	<= phase1;
	phase1_d1	<= phase1_d0;
end

wire	[31:0]	multi;
assign	multi	= (sin_dat2 > sin_dat1)? 
				(sin_dat2 - sin_dat1)*(phase_d1 - phase1_d1) : 
				(sin_dat1 - sin_dat2)*(phase_d1 - phase1_d1);

assign	sin_out	= (sin_dat2 > sin_dat1)? sin_dat1 + (multi >> 8) : sin_dat1 - (multi >> 8);

endmodule

  对这个模块的输出与对应的正弦函数真值进行比较，误差如下

可以看到误差急剧缩减到 $\pm 4$ ，相对误差只有 $1.22\times 10^{-4}$，大概万分之一。误差相较于相位下取整然后直接查找的方法缩小了 2 个数量级，而资源消耗仅仅增加了一个 16x256 的 rom，相较于 16x65536 rom 的恐怖资源消耗量可谓具有极高的性价比了。

正弦信号发生器

  懒得写了，看以后心情再补上这里。─=≡Σ(((つ•̀ω•́)つ