图（课堂笔记）

图的引入与术语

两种图

1. 有向图（Digraph）：Each edge of arc has an associated direction.

2. 无向图（non-directed graph）：Every edge or arc is two-way.

简单图是一种特殊的无向图。无向图没有自环(self-loop)和重复的边。

树

树是一个没有环（loop）的图。

有向图的表示

1. G=（N，A）

        N={ a, b, c }

        A={ (a,a), (a,c), (b,a),  (c,a), (c,b) }

2. G=( {a, b, c}, { (a,a), (a, c), (b,a), (c,a), (c,b) } )

术语

1. Weight：The number of nodes is sometimes called its weight.

2. (a, b)：Node "b" is said to be adjacent to node "a"; "a" is the out-node, b is the in-node.

3. Arc can't be duplicated：Can't have two (a, c), but can exist a (c, a).

4. Maximum possible number of arcs：If weight is w, maximum number of arcs  is w^2.

5. Full gragph：A directed graph contains the w^2 is called full graph.

6. Density：If there are a arcs and w nodes, the density is a/w^2.

7. Complementary Graph：The complementary graph of G called G*, which contains all the nodes of G and all the possible arcs not present in G.

Density(G*) =1 - Density(G).

(G*)*=G

8. Partial(Reduced) Graph：A partial (reduced) graph of G contains all the nodes of G, one or more arc deleted.

9. Subgraph： A subgraph of G contains one or more node deleted, all the arcs deleted which are associated with one or more of the deleted nodes.

10. Paths：A path of a graph G is an ordered set of nodes such that each node is adjacent to its predecessor. 

Path=(b,a,c,a,a)

arcs of Path=((b, a), (a, c), (c, a), (a, a))

11. Length：The number of arcs it contains

对于上面的Path，the length is 4.

12. Simple(elementary) path：The path which doesn't visit any node more than once.

(c, b, a) is a simple path.

13. Loop：A path whose initial and final nodes are the same.

(c, b, a, a, c) is a loop.

14. Simple Loop：A loop which becomes a simple path if its final node is deleted.

(c, b, a, c) is a simple loop.

15. Distance：The length of the shortest path between the nodes.

16. Diameter：The largest Distance which can be found in a graph.

G : ((b, a), (a, c)) and ((a, c), (c, b))

There are shortest paths of length 2.

None of length 3.

So the diameter of G is 2.

17. In and Out Degree：A node has degree(p,q) if p arcs point to it, and q arcs leave it.

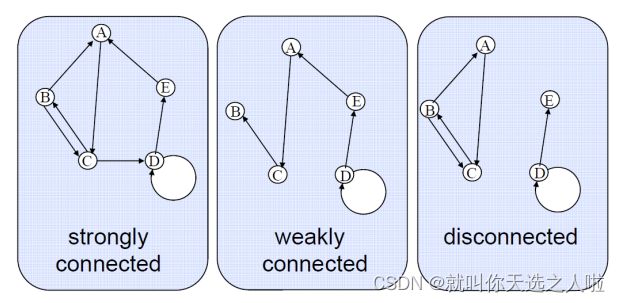
18. Connectivity：

Strongly Connected：一个有向图是强连通的，如果从图中的任意一个顶点出发，可以通过有向路径到达图中的任意其他顶点。

Weakly Connected：一个有向图是弱连通的，如果将有向图中的所有有向边都看作无向边后，所得到的无向图是连通的。

Disconnected：一个有向图是不连通的，如果其中至少存在两个顶点，这两个顶点之间无法通过有向路径相互到达。

对于无向图而言，既是连通的，也是非连通的，没有强弱连通的概念之分。