算法笔记 Restart
一、链表
双指针、快慢指针
翻转链表(递归):head.next.next = head; 对于不同问题迭代和递归相结合
寻找链表中点:快慢指针
二、数组
1.快慢指针:
- 原地修改数组问题:快指针碰到符合要求的再推进慢指针
2.左右指针:
- 二分查找
- 递增数组两数之和
3.前缀和数组:适用于快速、频繁地计算一个索引区间内的元素之和
class PrefixSum {
// 前缀和数组
private int[] prefix;
/* 输入一个数组,构造前缀和 */
public PrefixSum(int[] nums) {
prefix = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < prefix.length; i++) {
prefix[i] = prefix[i - 1] + nums[i - 1];
}
}
/* 查询闭区间 [i, j] 的累加和 */
public int query(int i, int j) {
return prefix[j + 1] - prefix[i];
}
}
4.差分数组:主要适用场景是频繁对原始数组的某个区间的元素进行增减。
如果想对区间 nums[i…j] 的元素全部加 3,那么只需要让 diff[i] += 3,然后再让 diff[j+1] -= 3 即可:
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
5.螺旋遍历矩阵(leetcode54、59):
- 遍历的圈数为 (Math.min(m,n)-1)/2
- 往回走时需要设置条件,只有一层时不应该往回走
6.O(1)时间复杂度实现数组的删除操作
把要删除的元素和数组末尾的元素交换,再删除数组末尾的元素
三、滑动窗口
- 子串问题(注意是包含还是排列,排列则加一个条件 right-left==s.length())
// 左闭右开,起始都为0
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
// 进行窗口内数据的一系列更新
...
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
// 进行窗口内数据的一系列更新
...
}
}
- 滑动哈希:RABIN KARP 字符匹配算法,在窗口移动过程中快速计算窗口中的hash值进行匹配
四、字符串
1.字符串转换为数字(O(1)复杂度字符串匹配)
/* 在最低位添加一个数字 */
int number = 8264;
// number 的进制
int R = 10;
// 想在 number 的最低位添加的数字
int appendVal = 3;
// 运算,在最低位添加一位
number = R * number + appendVal;
// 此时 number = 82643
/* 在最高位删除一个数字 */
int number = 8264;
// number 的进制
int R = 10;
// number 最高位的数字
int removeVal = 8;
// 此时 number 的位数
int L = 4;
// 运算,删除最高位数字
number = number - removeVal * R^(L-1);
// 此时 number = 264
位数通过字符编码确定。以 ASCII 码为例,ASCII 码其实就是 0~255 这 256 个数字,分别对应所有英文字符和英文符号。那么一个长度为 L 的 ASCII 字符串,我们就可以等价理解成一个 L 位的 256 进制的数字,这个数字就可以唯一标识这个字符串,也就可以作为哈希值。
五、二分查找
「使……最大值尽可能小」是二分搜索题目常见的问法。通常是找到某个值使得恰好满足题设条件,然后不断收缩边界,找到满足题设条件的最小值。
1.基本二分搜索
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
注意点:
- 搜索区间为左右闭区间 [left, right]
- while里 <=
- mid = left + (right - left) / 2; 防止整型溢出
- mid+1, mid-1
2.寻找左侧边界的二分搜索
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
// 此时 target 比所有数都大,返回 -1
if (left == nums.length) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
注意点:
- nums[mid] == target时收缩右侧边界
- 左侧边界最后返回的是left
- 返回前需要判断是否是目标值
3.寻找右侧边界的二分搜索
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这里改成收缩左侧边界即可
left = mid + 1;
}
}
// 最后改成返回 left - 1
if (right < 0) return -1;
return nums[right] == target ? right : -1;
}
注意点同左侧边界搜索
六、随机算法
1.带权重的随机算法(leetcode528)
前缀和+二分查找:生成一个线段,权重代表这个数在线段中的长短;在线段中随机选择一个点,这个点落在哪段上就选择哪个点

1、根据权重数组 w 生成前缀和数组 preSum。
2、生成一个取值在 [1, preSum[n - 1]] 之内的随机数(注意不包含0,0是preSum中的占位符),用二分搜索算法寻找大于等于这个随机数的最小元素索引(寻找左边界)。
3、最后对这个索引减一(因为前缀和数组有一位索引偏移),就可以作为权重数组的索引,即最终答案:
2.带黑名单的随机算法(leetcode710)
1、总共N个数,黑名单里m个数,在 [0,N-m) 中取随机数
2、把在 [0,N-m) 范围内的黑名单数映射到数组末尾的非黑名单数
3、取到的随机数如果不是黑名单数,返回该数;如果是黑名单数,返回映射值
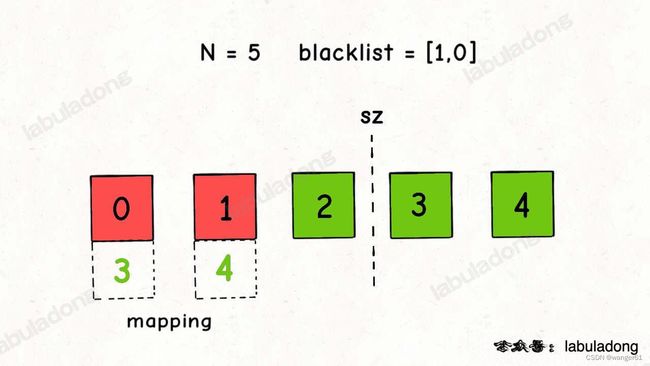
两个注意点:
- 映射到数组末尾的数不应该在黑名单内
- 不在 [0,N-m) 范围内的黑名单数不需要进行映射
七、树
二叉树问题的两种思维模式:
- 通过遍历一遍二叉树得到答案,在前、中、后序遍历位置进行相应操作
- 前序位置的代码在刚刚进入一个二叉树节点的时候执行;
- 后序位置的代码在将要离开一个二叉树节点的时候执行;
- 中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
- 通过递归的方式,将问题分解到子树
1.后序遍历
前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。一旦发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置进行处理。
2.层序遍历
// 输入一棵二叉树的根节点,层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 从上到下遍历二叉树的每一层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每一层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 将下一层节点放入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
3.二叉树的构造
先构造出根节点,再递归的构造左子树和右子树
根据前序遍历和后序遍历构造的树不唯一,且前序和后序的边界值都需要确认
4.序列化二叉树
使用哪种遍历方式进行序列化,再使用哪种方式进行反序列化即可
注意:一定要使用分隔符!分隔符最好用 “,”;
5.BST二叉搜索树
二叉搜索树中第K小的元素:
- O(N):中序遍历
- O(logN):每个节点有一个size熟悉记录以自己为根的这棵二叉树有多少个节点(有了该属性,即可通过node.left.size+1得到当前节点的排名)。查找排名为 k 的元素,当前节点知道自己排名第 m,那么我可以比较 m 和 k 的大小:
- 如果 m == k,显然就是找到了第 k 个元素,返回当前节点就行了。
- 如果 k < m,那说明排名第 k 的元素在左子树,所以可以去左子树搜索第 k 个元素。
- 如果 k > m,那说明排名第 k 的元素在右子树,所以可以去右子树搜索第 k - m - 1 个元素。
二叉搜索树的搜索框架
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
验证二叉搜索树(使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点)
boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
// base case
if (root == null) return true;
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if (min != null && root.val <= min.val) return false;
if (max != null && root.val >= max.val) return false;
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
return isValidBST(root.left, min, root)
&& isValidBST(root.right, root, max);
}
二叉搜索树删除节点
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node) {
// BST 最左边的就是最小的
while (node.left != null) node = node.left;
return node;
}
八、排序
1.归并排序
class Merge {
// 用于辅助合并有序数组
private static int[] temp;
public static void sort(int[] nums) {
// 先给辅助数组开辟内存空间
temp = new int[nums.length];
// 排序整个数组(原地修改)
sort(nums, 0, nums.length - 1);
}
// 定义:将子数组 nums[lo..hi] 进行排序
private static void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
// 单个元素不用排序
return;
}
// 这样写是为了防止溢出,效果等同于 (hi + lo) / 2
int mid = lo + (hi - lo) / 2;
// 先对左半部分数组 nums[lo..mid] 排序
sort(nums, lo, mid);
// 再对右半部分数组 nums[mid+1..hi] 排序
sort(nums, mid + 1, hi);
// 将两部分有序数组合并成一个有序数组
merge(nums, lo, mid, hi);
}
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
private static void merge(int[] nums, int lo, int mid, int hi) {
// 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
// 左半边数组已全部被合并
nums[p] = temp[j++];
} else if (j == hi + 1) {
// 右半边数组已全部被合并
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
leetcode315 计算右侧小于当前元素的个数:在对 nums[lo…hi] 合并的过程中,每当执行 nums[p] = temp[i] 时,就可以确定 temp[i] 这个元素后面比它小的元素个数为 j - mid - 1。递归的计算,每次merge都能计算当前递归中比temp[i] 小的元素个数,最终通过多次递归判定原数组中比temp[i] 小的元素个数。
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
arr[p] = temp[j++];
} else if (j == hi + 1) {
arr[p] = temp[i++];
// 更新 count 数组
count[arr[p].id] += j - mid - 1;
} else if (temp[i].val > temp[j].val) {
arr[p] = temp[j++];
} else {
arr[p] = temp[i++];
// 更新 count 数组
count[arr[p].id] += j - mid - 1;
}
}
2.快速排序
public static void sort(int[] nums) {
shuffle(nums);
sort(nums, 0, nums.length-1);
}
private static void sort(int[] nums, int lo, int hi){
if(lo >= hi){ return; }
int p = partition(nums, lo, hi);
sort(nums, lo, p-1);
sort(nums, p+1, hi);
}
private static int partition(int[] nums, int lo, int hi){
int pivot = nums[lo];
int i = lo + 1, j = hi;
while(i <= j){
while(i < hi && nums[i] <= pivot){ i++; }
while(j > lo && nums[j] > pivot){ j--; }
if(i >= j){ break; }
swap(nums, i, j);
}
swap(nums, lo, j);
return j;
}
private static void shuffle(int[] nums){
Random ran = new Random();
int n = nums.length;
for(int i=0; i<n; i++){
int r = i + ran.nextInt(n - i);
swap(nums, i ,r);
}
}
private static void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
TopK问题:
1)堆
2)二分查找 + partition
public int findKthLargest(int[] nums, int k) {
int l = 0;
int r = nums.length-1;
while(l <= r){
int p = partition(nums, l, r);
if(p == k - 1){ return nums[p]; }
else if(p > k - 1){
r = p - 1;
}else if(p < k - 1){
l = p + 1;
}
}
return 0;
}