Semi-supervised Learning(半监督学习)
目录
Introduction
Why semi-supervised learning help？
Semi-supervised Learning for Generative Model
Supervised Generative Model
Semi-supervised Generative Model
Low-density Separation Assumption
Self Training
Entropy-based Regularization(基于熵的正则化)
Semi-supervised SVM
Smoothness Assumption
cluster and then label
Graph-based Approach
Better Representation
Introduction
Supervised Learning（监督学习）：
Training data为
，每一笔data都有输入和输出（标签）。
- Semi-supervised Learning（半监督学习）
Training data 为
，其中部分data没有标签。通常情况下无标签的数据远远大于有标签的数据，即U>>R。
半监督学习可以分为以下两种：
- Transductive Learning（转换学习）：unlabeled data is the testing data，把testing data当做无标签的training data使用，适用于事先已经知道testing data的情况。
- Inductive Learning（归纳学习）：unlabeled data is not the testing data，不把testing data的feature拿去给机器训练，适用于事先并不知道testing data的情况(更普遍的情况)
- 为什么要做semi-supervised learning？
实际上我们不缺data，只是缺有label的data。
Why semi-supervised learning help？
unlabeled data虽然只有input，但它的分布，却可以告诉我们一些事情。以下图为例，在只有labeled data的情况下，红线是二元分类的分界线。但当我们加入unlabeled data的时候，由于特征分布发生了变化，分界线也随之改变。
semi-supervised learning的使用往往伴随着假设，而该假设的合理与否，决定了结果的好坏程度；比如上图中的unlabeled data，它显然是一只狗，而特征分布却与猫被划分在了一起，很可能是由于这两张图片的背景都是绿色导致的，因此假设是否合理显得至关重要。
Semi-supervised Learning for Generative Model
Supervised Generative Model
在监督学习中，进行分类训练时，我们首先会计算class1和class2的先验概率P(C1)
和P(C2)
,然后计算类条件概率P(x|C1)
与P(x|C2)
（假设它们服从高斯分布），最后计算后验概率P(C1|x)
。
Semi-supervised Generative Model
在基于监督模型的基础上，增加一些无标签的数据之后，就会发现之前那的μ和∑是不合理的，所以需要用无标签的数据重新估计。
具体步骤如下：
- 初始化class1和class2的均值、协方差矩阵以及先验概率，统称为θ。可以随机初始化，也可以用有标签数据估算。
- 根据θ计算出unlabeled data的后验概率。
- 更新参数。
以上的推导基于的基本思想是，把unlabeled data
看成一部分属于
，一部分属于
,则用全概率公式就可以求出x属于unlabeled data的概率。
Low-density Separation Assumption
通俗来讲，就是这个世界是非黑即白的，在两个class的交界处data的密度(density)是很低的，它们之间会有一道明显的鸿沟，此时unlabeled data(下图绿色的点)就是帮助你在原本正确的基础上挑一条更好的boundary。
Self Training
- 首先从labeled data去训练一个model
; - 用
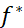对unlabeled data打上label，叫作pseudo label（伪标签）； - 从unlabeled data中拿出一些data加到labeled data里；
- 继续训练model
。
- self-training在regression上有用吗？
Regression的output是一个数值，因为unlabeled data代入模型变成labeled data，重新训练的模型不会发生改变。
该方法与之前提到的generative model还是挺像的，区别在于：
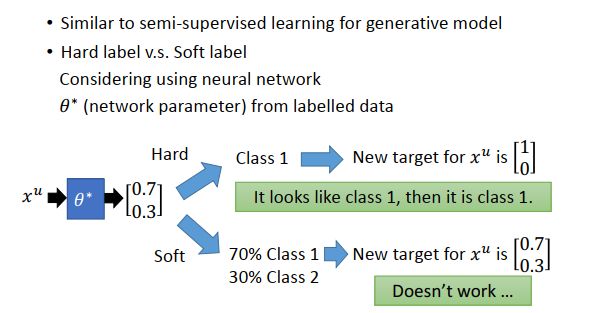
- Self Training使用的是hard label：假设一笔data强制属于某个class。
- Generative Model使用的是soft label：假设一笔data可以按照概率划分，不同部分属于不同class。
可以看到，在neural network里使用soft label是没有用的，因为把原始的model里的某个点丢回去重新训练，得到的依旧是同一组参数，实际上low density separation就是通过强制分类来提升分类效果的方法。
Entropy-based Regularization(基于熵的正则化)
这种方法是Self-training的进阶版。我们可以使用Entropy评估分布
的集中程度，Entropy越大分布越离散。反之则分布越集中。因此，在unlabeled data上，output的entropy要越小越好。
对labeled data来说，它的output要跟正确的label越接近越好，用cross entropy表示；对unlabeled data来说，要使得该output的entropy越小越好，两项综合起来，可以用weight来加权，以决定哪个部分更为重要一些。
Semi-supervised SVM
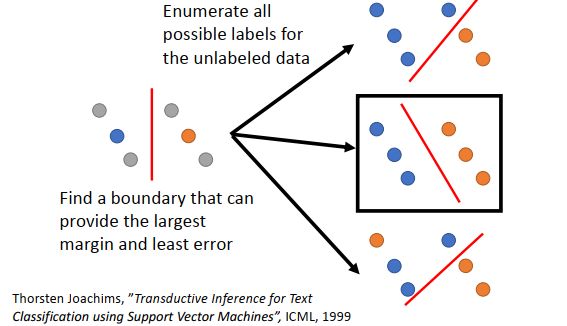
SVM为两个类别的数据找到一个boundary，一方面要有最大的margin，让这两个class分的越开越好；另一方面，要有最小的分类错误。
SVM穷举所有unlabled data的类别并进行计算，最终选择与两个类别的margin最大、分类错误最小的boundary。
但是这么做会存在一个问题，数据量大的时候，几乎难以穷举完毕。下面给出的paper提出了一种approximate的方法，基本精神是：一开始你先得到一些label，然后每次改一笔unlabeled data的label，看看可不可以让你的objective function变大，如果变大就去改变该label。
Smoothness Assumption
smoothness assumption的基本精神是：近朱者赤，近墨者黑。即相似的x
具有相同的y
，其具体定义为：
的分布是不平均的。- 如果今天x1和x2在一个高密度的区域很相似的话，
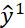和
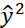才相同。
以手写数字识别为例，对于最右侧的2和3以及最左侧的2，显然最右侧的2和3在pixel上相似度更高一些；但如果把所有连续变化的2都放进来，就会产生一种“不直接相连的相似”，根据Smoothness Assumption的理论，由于2之间有连续过渡的形态，因此第一个2和最后一个2是比较像的，而最右侧2和3之间由于没有过渡的data，因此它们是比较不像的。人脸的过渡数据也同理。
Smoothness Assumption在文件分类上是非常有用的。假设对天文学(astronomy)和旅行(travel)的文章进行分类，它们有各自的专属词汇，此时如果unlabeled data与label data的词汇是相同或重合(overlap)的，那么就很容易分类；但真实情况中unlabeled data和labeled data之间可能没有任何重复的word，因为世界上的词汇太多了，sparse的分布中overlap难以发生。
但如果unlabeled data足够多，就会以一种相似传递的形式，建立起文档之间相似的桥梁。
cluster and then label
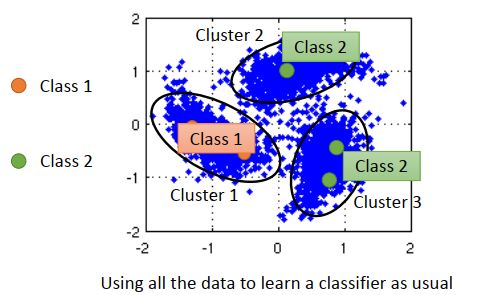
cl then label就是先聚类后标记。假设数据分布如下，橙色是class 1，绿色是class 2，蓝色是未标注数据。接下来做聚类，可能把所有数据分成3个cluster。在cluster1里，class 1的label最多，那cluster1里所有数据标记为class 1，同样的cluster2和cluster3都标记为class 2。然后把标记后的数据拿去learn。
Graph-based Approach
通过引入图结构，来表达通过高密度路径进行连接这件事情。所谓的高密度路径的意思是说，如果有两个点，在图上是相连的，那它们就是同一个class，如果没有相连，就算距离很近，也走不到。
- 如何构建图？
- 先定义两个对象之间的相似度
- 然后就是添加边，构建graph，方式有很多种： k nearest neighbor：计算数据与数据之间的相似度，然后设置k例如3，就是3个最相似的点相连。 e-Neighborhood：只有相似度超过某个阈值的点才会相连。
- 除此之外，还可以给Edge特定的weight，让它与相似度s成正比。
graph-based approach的基本思想就是，在graph上已经有一些labeled data，那么跟它们相连的point，属于同一类的概率就会上升，每一笔data都会去影响它的邻居，，并且这个影响是会随着edges传递出去的。但是如果数据不够多，中间就有断开，那信息就传递不过去。
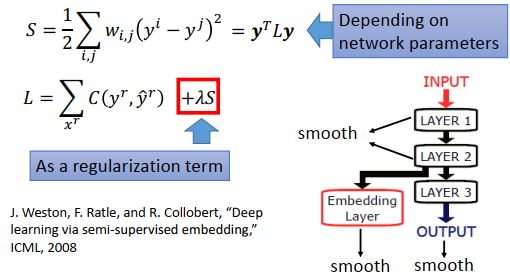
然后定义一个S函数，定量分析graph的平滑度，数值越小表示越滑。
S可以稍微整理下，写成向量形式如下图。
如果要把平滑度考虑到神经网络里时，就是在原来的损失函数里加上
。不一定要在output上计算平滑度，在深度神经网络里，可以把平滑度计算放在网络的任何地方。
Better Representation
Better Representation的精神是，去芜存菁，化繁为简。就是要抓住核心。