6. 神经网络
6.1 非线性假设
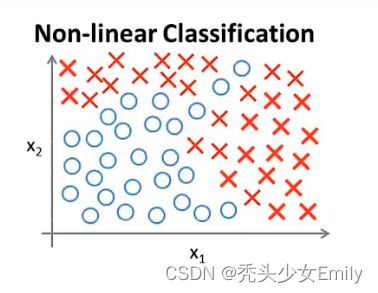
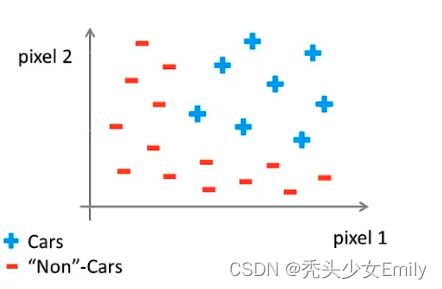
假设有一个监督学习分类问题,训练集如图
如果利用logistic回归来解决这个问题,我们可以构造一个包含很多非线性项的logistic回归函数。
但在这个训练集只给出了两个特征,如果一旦特征变多了,多项式就会变得很多。就会出现过拟合、计算量大的问题。
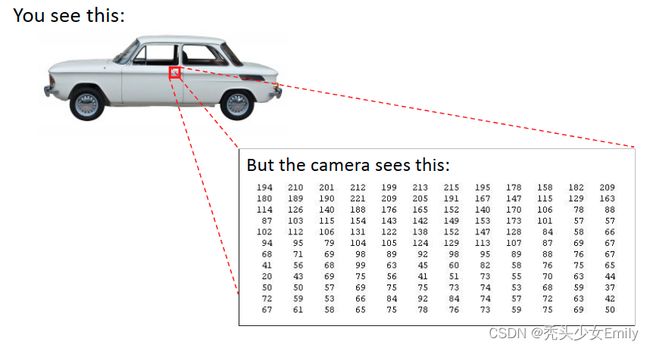
以识别一张图片是否为汽车为例子:
对于识别图像中的一个门把手,对于我们人来说一下子就能看出来,但是对于计算机则是要通过一个像素亮点矩阵来告诉我们这些数值代表一个汽车门把手。
具体说来,用机器学习算法构造一个汽车识别器时,我们要做的就是提供一个带标签的样本集,其中一些样本是各类汽车,另一部分样本不是车,将这个样本集输入给学习算法来训练出一个分类器。然后我们进行测试,输入一幅新的图片,让分类器判定这是什么东西,理想情况下是能识别出是什么。
假设我们用的图片像素为50 * 50,有2500个像素点,因此特征向量N为2500。这还是在使用灰色图像的情况下,如果是RGB彩色图像,则有7500个像素点。
在简单的非线性假设上,使用logistic回归是没有问题的 ,但是在复杂的非线性假设上就不太适用了。而这个时候,神经网络在学习复杂的非线性假设上被证明是一种好得多的算法。
6.2 神经元与大脑
神经网络的起源:人们想设计出模仿大脑的算法,它的理念就是如果我们想要建立学习系统,那为什么不去模仿我们所认识的、最神奇的学习机器——人类的大脑呢?
讲述了一些大脑学会“看”“听”的例子
6.3 模型展示
在运用神经网络时,我们该如何表示我们的假设或模型?
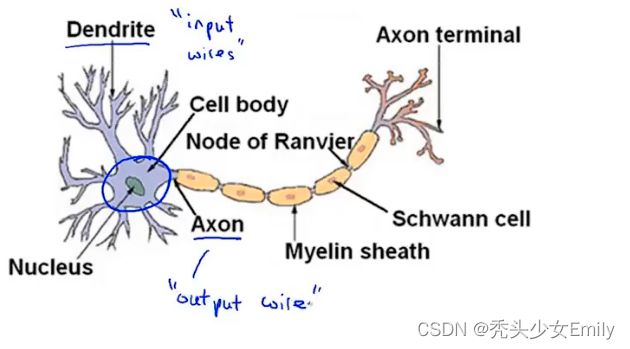
神经网络模仿了大脑中的神经元或者神经网络,为了解释如何表示假设模型
简而言之:神经元是一个计算单元,它从输入通道接受一定数目的信息并做一些计算,然后将结果通过它的轴突(Axon)传送到其他节点或者大脑中的其他神经元。
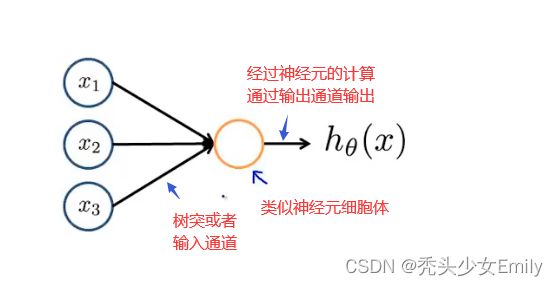
现在我们将神经元模拟成一个逻辑单元
一般就会写出三个参数,有时候会额外添加一个参数:![]() ,有时也被称作偏置单元或者偏置神经元。但因为
,有时也被称作偏置单元或者偏置神经元。但因为![]() 总是等于1,有时候会表达出来有时候不会,取决于具体例子。
总是等于1,有时候会表达出来有时候不会,取决于具体例子。
关于神经网络的术语:
- 有时我们会说上述的逻辑单元是一个带有sigmoid或者logistic激活函数的人工神经元。其中激活函数是指非线性函数
 的另一个术语。
的另一个术语。 - 我们之前所使用的
 参数集合都是默认说是模型的参数,但在有一些文献里面也被称为权重,但两者其实是一样的东西。
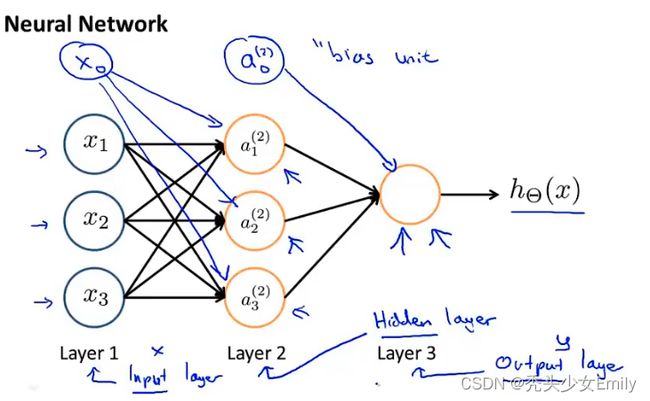
参数集合都是默认说是模型的参数,但在有一些文献里面也被称为权重,但两者其实是一样的东西。 - 在网络中的第一层也被称作为输入层,最后一层则被称作输出层,中间层第二层被称为隐藏层(在下图所示的例子中)
上面途中所表示的只是单个神经元,但其实神经网络就是一组神经元连接在一起的集合。具体来说,下图是我们的输入单元是![]() (可以额外加
(可以额外加![]() ),紧接着是三个神经元
),紧接着是三个神经元![]() (也可以额外加
(也可以额外加![]() ),最后的一个节点进行计算并输出。
),最后的一个节点进行计算并输出。
为了更好的解释这个神经网络的具体步骤,还需要记一些记号:
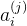 :表示第j层第i个神经元或单元的激活项(激活项是指由一个具体的神经元计算并输出的值)
:表示第j层第i个神经元或单元的激活项(激活项是指由一个具体的神经元计算并输出的值)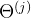 :神经网络被这些矩阵参数化也就是
:神经网络被这些矩阵参数化也就是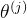 ,权重矩阵。它控制从某一层,比如说从第一层到第二层或者第二层到第三层的映射的参数矩阵。
,权重矩阵。它控制从某一层,比如说从第一层到第二层或者第二层到第三层的映射的参数矩阵。
下面是计算的过程
如果一个网络在第j层有![]() 个单元,在j+1层有
个单元,在j+1层有![]() +1个单元,那么矩阵
+1个单元,那么矩阵![]() 即控制第j层到第j+1层的映射的矩阵,它的维度是
即控制第j层到第j+1层的映射的矩阵,它的维度是![]() ,就比如上图的
,就比如上图的![]() 就是3X4的矩阵。
就是3X4的矩阵。
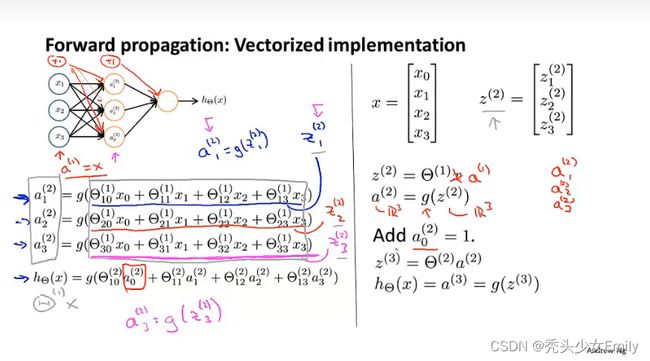
神经网络的向量化:
在这里的输入层的x可以更换成![]() ,在上图中的计算过程被称作前向传播,这样叫的原因是:我们从输入单元的激活项开始,然后进行前向传播给隐藏层,计算隐藏层的激活项,继续前向传播并计算输出层的激活项。这个依次计算激活项,从输入层到隐藏层再到输出层的过程叫前向传播。
,在上图中的计算过程被称作前向传播,这样叫的原因是:我们从输入单元的激活项开始,然后进行前向传播给隐藏层,计算隐藏层的激活项,继续前向传播并计算输出层的激活项。这个依次计算激活项,从输入层到隐藏层再到输出层的过程叫前向传播。
如果把输入层遮住,只看隐藏层和输出层,会发现很像逻辑回归。表面上是类似的,但实际上是不同的,因为输入的特征变化了,逻辑回归的输入特征是x而神经网络的输入变成了处理后的a。
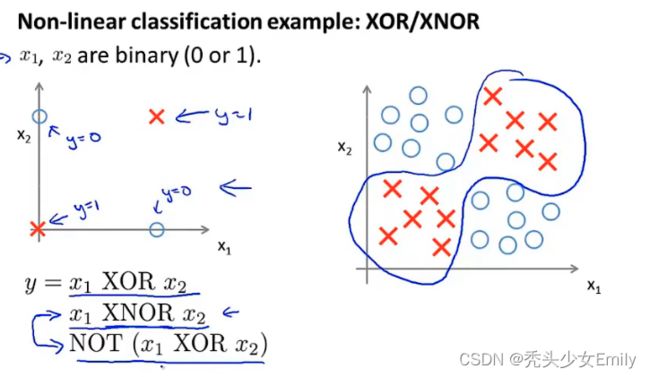
6.4 神经网络计算的例子
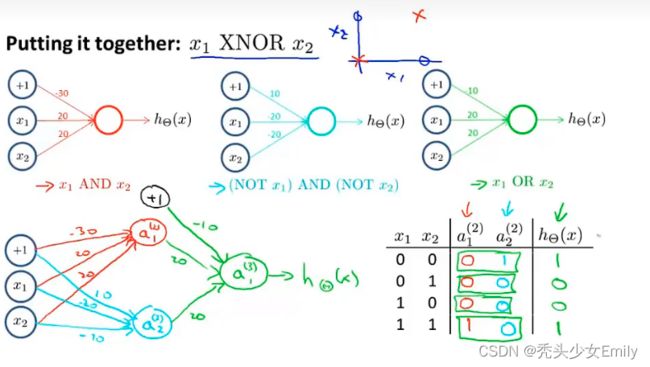
XOR(异或):相同为0,相异为1;XNOR:相同为1,相异为0。
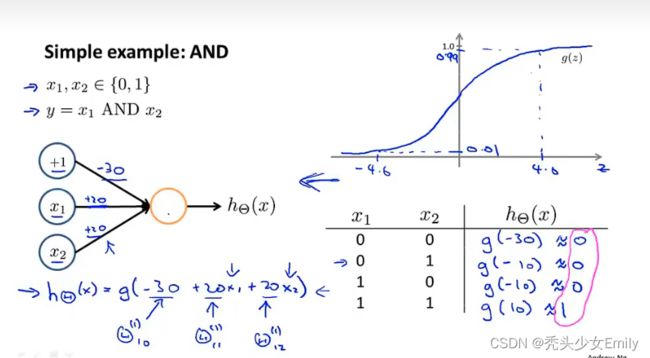
先从AND开始理解:假设有2个二进制的输入![]() ,
,![]()
可以看到右下角的真值表,会发现是逻辑与的结果
再来看看逻辑或
结合上面的,现在来推演XNOR
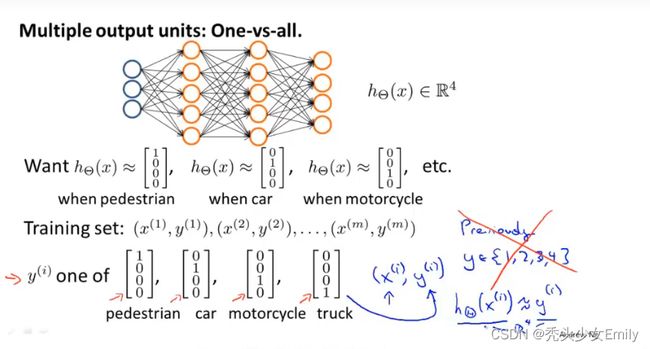
 6.5 多元分类
6.5 多元分类
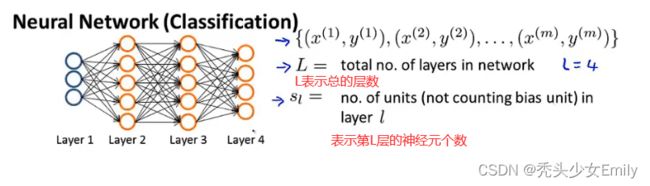
6.6 代价函数
重点会放在神经网络在分类问题中的应用。
代价函数:
logistic regression(逻辑回归):
大括号后面那一项是额外的正则项,因为我们并没有把偏差项![]() 正则化,所以j从1到n。
正则化,所以j从1到n。
Neural network(神经网络):
![]() ,
,![]()
其中:l代表层数、i代表当前层的输入参数个数、j代表当前的单元数;L表示第几个层,![]() 表示当前的输出层的,
表示当前的输出层的,![]() +1表示输出的个数(即几个y)。
+1表示输出的个数(即几个y)。
6.7 反向传播算法
利用梯度下降或者其他什么高级优化算法,我们需要做的就是写一段代码,获得输入参数![]() ,然后计算
,然后计算![]() ,和偏导项。
,和偏导项。
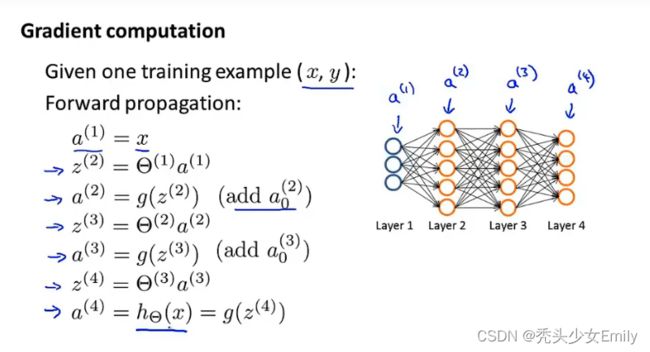
当我们只有一个训练样本的情况时,也就是一个实数对(x, y),我们来看看计算的顺序是什么。首先我们应用前向传播方法来计算在给定输入时,假设函数是否会真的输出结果。具体地说,这里的![]() 就是第一层的激活值,然后我们来计算
就是第一层的激活值,然后我们来计算![]() ,紧接着
,紧接着![]() ,g是一个sigmoid激活函数,一直重复上述步骤,具体过程如下图。
,g是一个sigmoid激活函数,一直重复上述步骤,具体过程如下图。
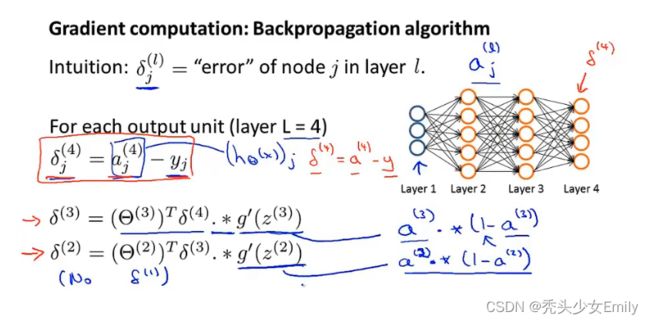
而反向传播算法从直观上说就是对每个结点,我们计算这样一项![]() ,就用这种方式代表了第l层第j个结点的误差。
,就用这种方式代表了第l层第j个结点的误差。![]() 则表示第l层第j个单元的激活值。这个
则表示第l层第j个单元的激活值。这个![]() 项从某种意义上就捕捉到了我们在这个神经结点的激活值的误差,所以我们可能希望这个结点的激活值稍微不一样。具体地讲,我们用下图有四层的神经网络结构作为例子。
项从某种意义上就捕捉到了我们在这个神经结点的激活值的误差,所以我们可能希望这个结点的激活值稍微不一样。具体地讲,我们用下图有四层的神经网络结构作为例子。
计算过程如下:对于每一个输入单元,我们将计算![]() 项,所以第四层的第j个单元的
项,所以第四层的第j个单元的![]() = 第j单元的激活值 - 训练样本第j个元素的真实值0。所以
= 第j单元的激活值 - 训练样本第j个元素的真实值0。所以![]() 项可以写成
项可以写成![]() 。所以
。所以![]() 这一项就是假设的输出值和训练集y值之间的差。
这一项就是假设的输出值和训练集y值之间的差。
第一层是输入的值,不用考虑误差项。
总结一般情况的反向传播算法:
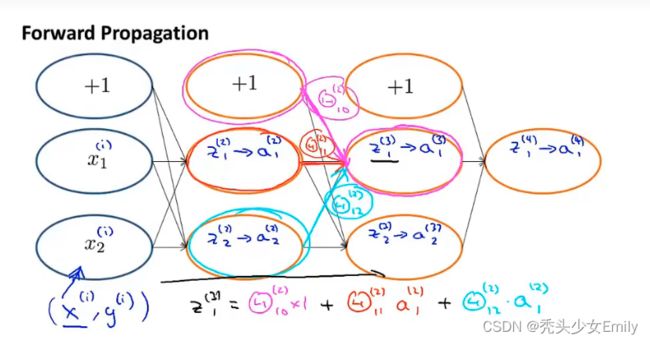
为了更好的研究反向传播算法步骤,先来研究一下前向传播的过程
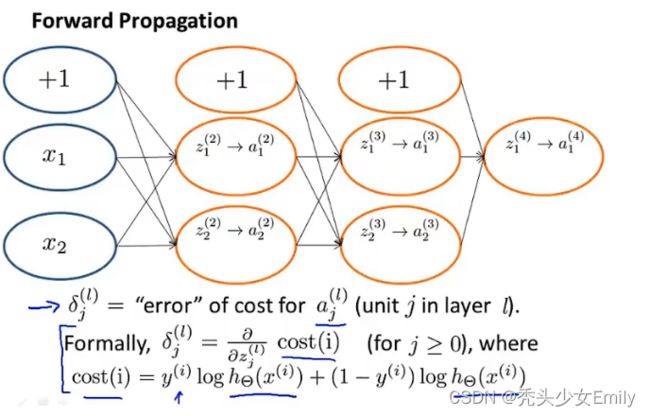
再来看看代价函数
cost(i)是针对的是最后一层的总误差,所以我们得通过这种递推的方法往前推,求解最后的误差和倒数第三层,倒数第四层那些中间值的关系,直到我们得到了最后的误差和所有中间值的关系。
并且这个小delta不是对theta的导数,是对激活输入的导数。
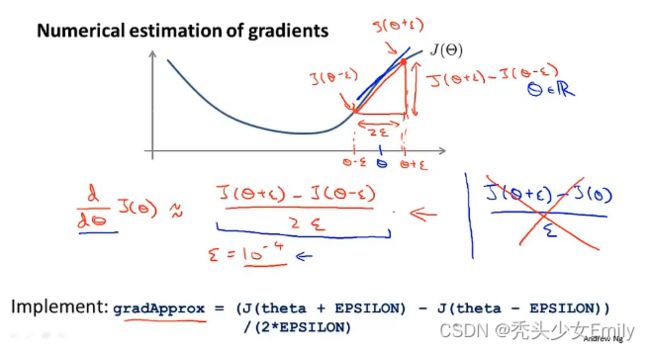
6.8 梯度检验
当反向传播和梯度下降结合时,往往会存在一些微妙的bug,这个时候就需要梯度检验来解决这些问题。
![]() 为实数时
为实数时
更一般的情况
实现梯度检验的过程:
- 通过反向传播来计算DVec(可能是矩阵
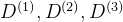 展开的形式)
展开的形式) - 实现数值上的梯度检验,计算出gradApprox
- 确保Dvec与gradApprox都能得出相似的值,确保它们只有几位小数的差距
- 在使用代码进行学习或说训练网络之前,重要的是关掉梯度检验。不要再去用之前的导数计算公式来计算导数gradApprox。上面说的梯度检验代码是一个计算量非常大的、非常慢的计算导数的程序。在反向传播那里讲述的计算Dvec的方法,是一个高性能的计算导数的方法,一旦你通过检验确定反向传播的实现是正确的,就应该关掉梯度检验。
6.9 随机初始化
当你执行一个算法,例如梯度下降法或者高级优化算法时,我们需要为变量![]() 选取一些初始值。对于高级优化算法,它默认你会为变量
选取一些初始值。对于高级优化算法,它默认你会为变量![]() 提供一些初始值。对于梯度下降法,我们同样耶需要对
提供一些初始值。对于梯度下降法,我们同样耶需要对![]() 进行初始化,初始化完毕后,我们就可以一步一步通过梯度下降来最小化代价函数J。
进行初始化,初始化完毕后,我们就可以一步一步通过梯度下降来最小化代价函数J。
那么问题来了,怎么样初始化呢?
有一种想法是,将![]() 全部设为0,在逻辑回归可能合适,但是在神经网络里起不到任何作用。所以,在神经网络中要使用初始化的思想。
全部设为0,在逻辑回归可能合适,但是在神经网络里起不到任何作用。所以,在神经网络中要使用初始化的思想。
为了训练神经网络应首先要将权重随机初始化为一个接近0的范围在![]() 到
到![]() 之间的数,然后进行反向传播,再进行梯度检验,最后使用梯度下降或者其他高级优化算法来最小化代价函数J这个给关于
之间的数,然后进行反向传播,再进行梯度检验,最后使用梯度下降或者其他高级优化算法来最小化代价函数J这个给关于![]() 的函数。
的函数。
6.10 回顾总结
在训练一个神经网络时,我们要做的第一件事就是选择一种网络架构(这里的就结构表示神经元之间的连接模式),你可以选择每一层有多少个隐藏单元以及有多少个隐藏层的架构。
- 首先我们定义了输入单元的数量,一旦你确定了特征集x输入单元的数量就等于特征
 的维度,输入单元数目将会由此确定。如果是正在进行多类别分类,那么输出层的单元数目将会由你分类问题中所要区分的类别个数确定。(如果你的多元分类问题,y的取值范围是1-10之间,那么你就有10个可能的分类,要把y重新写成向量的形式,如果其中一个样本被分到第五类也就是说y=5,那么在神经网络中,就不能直接用5来表达,而是用向量
的维度,输入单元数目将会由此确定。如果是正在进行多类别分类,那么输出层的单元数目将会由你分类问题中所要区分的类别个数确定。(如果你的多元分类问题,y的取值范围是1-10之间,那么你就有10个可能的分类,要把y重新写成向量的形式,如果其中一个样本被分到第五类也就是说y=5,那么在神经网络中,就不能直接用5来表达,而是用向量![[0, 0, 0, 0, 1, 0, 0, 0 ,0 ,0]^T](http://img.e-com-net.com/image/info8/32d1be959c2f4ed88523d7fa63ced80a.png) 表达)
表达) - 对于隐藏层单元的个数以及隐藏层的数目,一个合理的默认选项是只使用单个隐藏层。如果你要使用多个有隐藏层,同样也有一个合理的默认选项:就是每一个隐藏层通常都应该有相同的单元数。(隐藏层单元个数越多越好,但是越多也意味着计算量越大,并且要与输入特征数量相同或者大几倍都是可以的)
训练神经网络的步骤:
- 构建一个神经网络,然后初始化权重,通常会把权重初始化为很小的值接近于0
- 执行前向传播算法,也就是对该神经网络的任意一个输入的
 计算出对应的
计算出对应的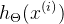 ,也就是输出值y的向量
,也就是输出值y的向量 - 通过代码计算出代价函数
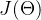
- 执行反向传播算法来偏导数项
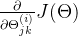
- 使用梯度检验来比较这些已经计算得到的偏导数项
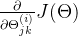 ,把用反向传播算法得到的偏导数值与用数值方法得到的估计值进行比较。因此通过进行梯度检验来确保两种方法得到基本接近的两个值。在确定用梯度检验后得到的结果是正确之后,停用梯度检验
,把用反向传播算法得到的偏导数值与用数值方法得到的估计值进行比较。因此通过进行梯度检验来确保两种方法得到基本接近的两个值。在确定用梯度检验后得到的结果是正确之后,停用梯度检验 - 最后我们可以使用一个最优化算法,比如说梯度下降算法或者更加高级的优化方法(LBFGS算法、共轭梯度法或者其他内置到fminunc函数中的方法)将这些优化算法和反向传播算法相结合,反向传播计算出这些偏导数项
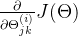 的值,再使用某个最优化方法来最小化关于
的值,再使用某个最优化方法来最小化关于 的代价函数
的代价函数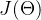 (神经网络的代价函数
(神经网络的代价函数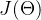 是一个非凸函数,因此理论上可能停留在局部最小值的位置。实际上,梯度下降算法和其他一些高级优化方法理论上都可能收敛于局部最小值。但是一般来讲,实际操作中这不是大问题)
是一个非凸函数,因此理论上可能停留在局部最小值的位置。实际上,梯度下降算法和其他一些高级优化方法理论上都可能收敛于局部最小值。但是一般来讲,实际操作中这不是大问题)
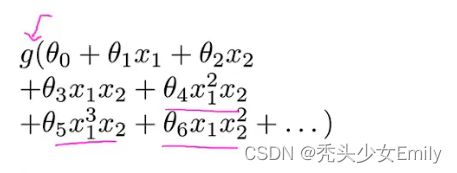
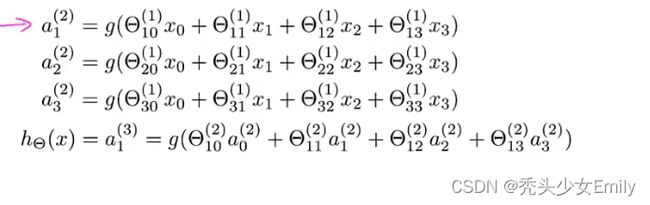


![J(\theta) = -\frac{1}{m}\left [ \sum_{i=1}^{m}y^{(i)}\log h_{\theta}(x^{(i)}) + (1-y^{(i)}) \log (1-h_{\theta}(x^{(i)})) \right ] + \frac{\lambda }{2m}\sum_{j=1}^{n}\theta_{j}^{2}](http://img.e-com-net.com/image/info8/4c8435c291da490fac23bc764d4daf6a.png)